|
《解説》 ■ ここでは,絶対値記号の処理について,応用範囲の広い2つの方法を紹介します.1つは,場合分けによって絶対値記号をはずす方法,もう1つはグラフを利用する方法です. ■1 場合分けによって絶対値記号をはずす方法 [定義] 数直線上で,xが表わす点と原点との間の距離を|x|で表わします. (正の数xについては,絶対値記号は「ただで取れます」.負の数は符号を変えます.)
《要点》
|
[?] 0は大きい方に含めなければならないか
|
《重要》
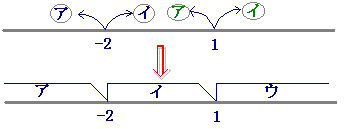
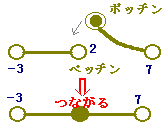
中身全体が+,0になるか−になるかで分類します. |
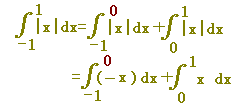 とします.
とします.


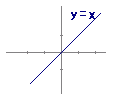 折り返す→
折り返す→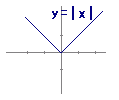 下に1移動→
下に1移動→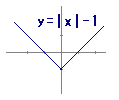 折り返す→
折り返す→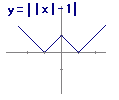 下に1移動→
下に1移動→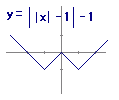 折り返す→
折り返す→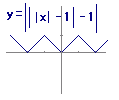
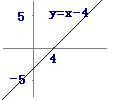 ==>
==>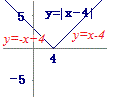 ==>
==>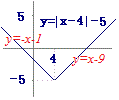 ==>
==>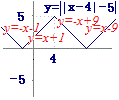 ・・・(答)
・・・(答)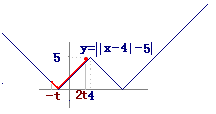

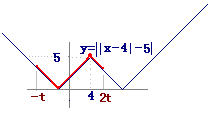 イ
イ
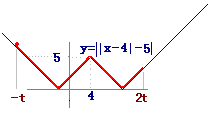 ウ
ウ
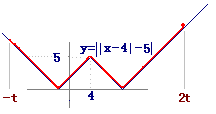 エ
エ
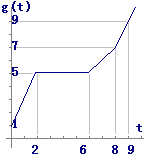 ・・・グラフ(答)
・・・グラフ(答)
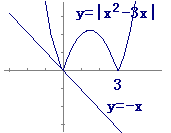 答案
答案
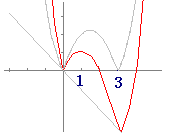
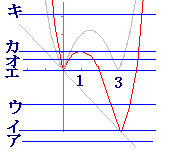
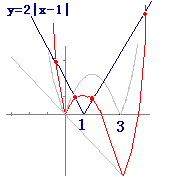 (2) 右の図により
(2) 右の図により




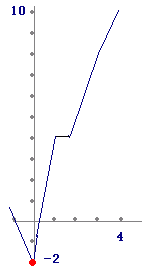
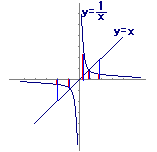 = = >
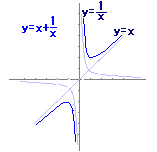
= = >
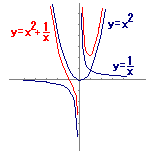
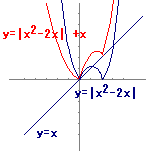
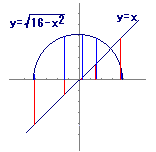 ==>
==>