|
○ 一般に、因数分解は次数が高くなるほど難しくなるので、2文字以上を含む多項式の因数分解では「次数が最も低い文字について整理する」のが有利となる。 ただし、この頁の問題はxについて整理しても、yについて整理しても2次となって同じになるので、xについて整理した形で途中経過を考えている。 ○ xについて整理するとは、xだけを文字と考え、他の文字yを係数、数字として扱うことをいう。 【例】 2x2+7xy+3y2−x+2y−1 ⇒ 2x2+7xy+3y2−x+2y−1 この式においてxだけを文字と考えると,係数2 , 7y , 3y2 , −1, 2y , −1の中で同類項(文字の部分が同じもの)は2種類ある: 7xyと−x、3y2と2yと−1 同類項は整理する(係数をまとめる): 2x2+(7y−1)x+(3y2+2y−1) このように変形すると、「たすき掛け因数分解」として、掛けると2になる2つの数(1と2)および掛けると3y2+2y−1となる2つの数(ここではyも数字、係数として扱っているからyを含む式を考える。  掛けると3y2+2y−1となる式を考えるとは,3y2+2y−1を因数分解しておくということ:(3y−1)(y+1) 掛けると3y2+2y−1となる式を考えるとは,3y2+2y−1を因数分解しておくということ:(3y−1)(y+1)
|
このように準備しておいて、前2つ、後ろ2つの係数の組合せのうちで、1次の係数が7y−1に一致するものを探す。 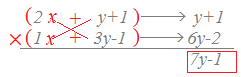 |