|
← PC用は別頁
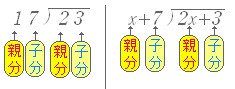
■ここだけの話■ このページでは,話をわかりやすくするために 37 のような数字では上の位の数字( 3 )を親分,下の位の数字( 7 )を子分とする. また,3x+7 のような多項式では,次数の高い方( 3x )を親分,次数の低い方( 7 )を子分とする. 2x2+5x−1 のような2次式では,親分は 2x2,子分は 5x ,−1とする. |
 |
| ○ 数字の割り算と多項式の割り算では,似ているところと似ていないところがある
○ 商の立て方 ・・・似ていない
(1) 次のような数字の割り算で,商として立てる数を考えるとき 「17が何個入っているか」と考える. 2の中に17は入っていないから,2の上には何も書かない. 23の中に17は1つ入るから,3の上に1と書く. ⇒ 「親分も子分も含めて何倍入るか」を考える (2) 次のような多項式の割り算では,とにかく「次数の高い項を消す」ことを考え,何が立つかを考える 2xを消すにはxに2を掛けるとよいので,2の上に2と書く. ⇒ 「割られる方の親分のことだけを考える」 ⇒ 「親分同士で何倍あるか決める」 (※ 子分のことを考えずに決めるので,いずれ,しわ寄せは子分に来る.・・・どうなるかは,後で分かる*) |
 数字を10進法と見れば,多項式は x 進法と見なせるところは似ているが,似ているのはそこまで.  |
|
○ 掛けるときは親分にも子分にも掛ける ・・・似ている
(1)(2) 数字のときも多項式のときも,商を立てた後のかけ算は親分にも子分にも全員に掛ける. |
数の割り算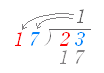 多項式の割り算 多項式の割り算
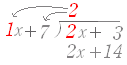 |
|
○ 割り算の中身は引き算 ・・・似ている
(1)(2) 数字のときも多項式のときも,割り算の中で組み立てている式は引き算.間違うおそれのあるときは, -) と書いてもよい. |
数の割り算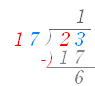 多項式の割り算 多項式の割り算
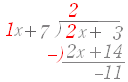 |
| * 数字の割り算では,「余り」や「係数」が負の数になることはないが,多項式の割り算では「親分の都合だけで商を立てる」ので,次の「多項式の割り算」の結果のように余りが負の数になることもある.(親分のつけは,子分が尻ぬぐい.)・・・似ていない |
|
【多項式の割り算(まとめ)】
[準備] 1. 割る式も割られる式も降べきの順に整理しておく. (必ず,次数の高い方から順に割ること) 
2. 割られる式で,ない項はあけておく. (初め(係数が0で)空いていても,途中で登場するのが普通なのであけておかないと計算がもつれてしまう) 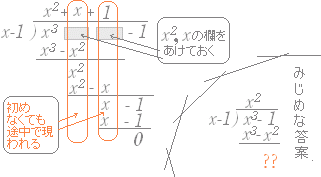
[商の立て方] 3. 割られる式の親分を消すために,割る式の親分に掛ける数を考える. (割られる方の親分を消すことだけを考える.そのためには,係数に「負の数」「分数」など必要なものは何でも使う.) 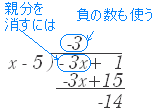
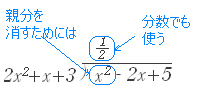
[割り算の中身の計算] 4. 掛けるときは親分にも子分にも全員に掛ける.
数の割り算
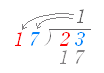 多項式の割り算 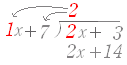 5. 割り算の中身は引き算
数の割り算
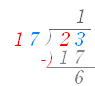 多項式の割り算 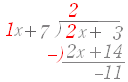 [どこまでやるかの判断] 6. 割られる方の次数が割る式よりも小さくなれば終了 (割られる方の次数が割る方と同じ次数なら,まだ計算途中と考える.) 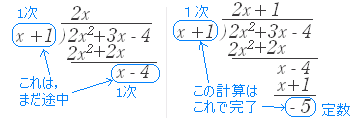
|