← PC用は別頁

== 円の方程式 ==
■　陰関数表示とは
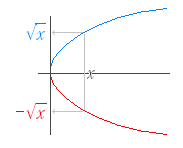
○　下図１の直線の方程式は
____________y=x−1 …(1)

のようにy について解かれた形で表されることが多いが，
____________x−2y−2=0 …(2)
のように x,y の関係式として表されることもある．

○　(1)のように，
____________y=f(x)
の形で，y について解かれた形の関数を陽関数といい，(2)のように
____________f(x,y)=0
という形で x,y の関係式として表される関数を陰関数という．

■　点が曲線上にあるとは
　方程式が(1)(2)どちらの形であっても，x=−1, 0,1,2,… を順に代入していくと，y=−,−1 ,−,0,… が順に求まり，

これらの点を結ぶと直線が得られる．一般に，ある点が与えられた方程式を表されるグラフ（曲線や直線）上にあるかないかは，次のように調べることができる．

○
ある点 (p,q) が y=f(x)のグラフ上にある⇔q=f(p)
ある点 (p,q) が y=f(x)のグラフ上にない⇔q≠f(p)
○
ある点 (p,q) が f(x,y)=0のグラフ上にある⇔f(p,q)=0
ある点 (p,q) が f(x,y)=0のグラフ上にない⇔f(p,q)≠0
図１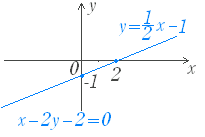
陽関数の例
y=2x+1, y=3x2, y=4
陰関数の例
y−2x−1=0, y−3x2=0, y−4=0
図２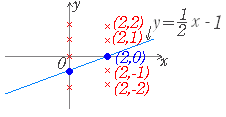
図２において
2≠×2−1だから(2,2)はy=x−1上にない．
1≠×2−1だから(2,1)はy=x−1上にない．
 0=×2−1だから(2,0)はy=x−1上にある．
 −1≠×2−1だから(2 ,−1)はy=x−1上にない．
−2≠×2−1だから(2 ,−2)はy=x−1上にない．
 陰関数で表示されているときも同様に，「代入したときに方程式が成り立てばグラフ上にある」「代入したときに方程式が成り立たなければグラフ上にない」と判断できる．
2−2×2−2≠0 だから (2,2) は x−2y−2=0 上にない．
2−2×1−2≠0 だから (2,1) は x−2y−2=0 上にない．
 2−2×0−2=0 だから (2,0) は x−2y−2=0 上にある．
 2−2×(−1)−2≠0 だから x−2y−2=0 上にない．
2−2×(−2)−2≠0 だから x−2y−2=0 上にない．

■　１つの x に対応する y が２つあるとき
○　下図３のように，１つの x に対応する y が２つあるグラフの方程式は，y=f(x) の形（陽関数）で書けば
y= と y=−
すなわち，
y= ±
となり，１つの陽関数 y=f(x) にはまとめられない．（y が２つあるから）
　陰関数を用いれば，y2=x あるいは x−y2=0 と書くことができる．

○　下図４は原点を中心とする半径５の円のグラフであるが，この円は縦線と２箇所で交わるので，１つの x に対応する y が２つあり，円の方程式は１つの陽関数では表せない．

○　下図５において，原点を中心とする半径５の円の方程式を求めてみよう．
　円周上の点 P の座標を (x,y) とおくと，ピタゴラスの定理（三平方の定理）により，
x2+y2=52 …(A)
が成り立つ．
　上半円については，y≧0 なので，
y= …(B)
　下半円については，y≦0 なので，
y=− …(C)
と書けるが，通常は円の方程式を(A)の形で表す．
※　点 (3, 4) は，32+42=52 を満たすのでこの円周上にある．
　また，点 (3,−4) も，32+(−4)2=52 を満たすのでこの円周上にある．
　さらに，点 (1, 2) も，12+(2)2=52 を満たすのでこの円周上にある．
　しかし，点 (3, 2) は，32+22=13≠52 を満たすのでこの円周上にないことが分かる．
　
図３
図４
図５

■　円の方程式
　原点を中心とする半径 r の円（円周）の方程式は
x2+y2=r2 …(1)
　点 (a,b) を中心とする半径 r の円（円周）の方程式は
(x−a)2+(y−b)2=r2 …(2)

※　初歩的な注意
○　(2)において，点 (a,b) を中心とする半径 r の円の方程式が
(x−a)2+(y−b)2=r2
点 (−a ,−b) を中心とする半径 r の円の方程式が
(x+a)2+(y+b)2=r2
点 (a ,−b) を中心とする半径 r の円の方程式が
(x−a)2+(y+b)2=r2
のように，中心の座標 (a,b) は，円の方程式では見かけ上の符号が逆になる点に注意．

○　(1)(2)とも右辺は r2 なので，
半径が 2 → 右辺は 4
半径が 3 → 右辺は 9
半径が 4 → 右辺は 16
半径が → 右辺は 2
半径が → 右辺は 3
などになる点に注意
（証明）
(1)←
　原点を中心とする半径 r の円周上の点を P(x,y) とおくと，直角三角形の横の長さが x，縦の長さが y の直角三角形の斜辺の長さが r となるのだから，
x2+y2=r2
が成り立つ．
　（別の証明）：２点間の距離の公式

　２点 A(a,b), B(c,d) 間の距離は，
を用いても，直ちに示せる．
　=r より x2+y2=r2

※　点 P が座標軸上（通俗的に言えば，赤道上または北極，南極の場所）にあるとき，直角三角形にならないが，たとえば x 軸上の点 (r,0) についても，r2+02=r2 が成り立つ．このように，座標軸上の点については直角三角形はできないが，この方程式は成り立つ．

※　点 P が第２，第３，第４象限にあるとき，x,y 座標が負になることがあるので，正確に言えば，直角三角形の横の長さが |x|，縦の長さが |y| とすべきであるが，このように説明すると経験上，半数以上の生徒が授業を聞く意欲をなくすようである（絶対値アレルギー?）．(1)においては，x,y が正でも負でも２乗するので結果はこれでよい．

(2)←
　２点 A(a,b), P(x,y) 間の距離は， 　だから，この値が r に等しいことが円周上にある条件となる．
=r より
(x−a)2+(y−b)2=r2
【例題】
(1)　原点を中心とする半径4の円の方程式を求めよ．

（解答）　x2+y2=16

(2)　点 (−5,3) を中心とする半径 2 の円の方程式を求めよ

（解答）　(x+5)2+(y−3)2=4
(3)　円 (x−4)2+(y+1)2=9 の中心の座標と半径を求めよ．

（解答）　中心の座標 (4 ,−1)，半径 3

【問題１】　次の円の方程式を求めてください．（選択肢の中から正しいものをクリック）
(1)
原点を中心とする半径3の円の方程式

(2)
点を中心とする半径の円の方程式

(3)
点を中心とする半径5の円の方程式

(4)
点を中心とする半径3の円の方程式

■　円の方程式の一般形（展開形）
x2+y2+Ax+By+C=0 …(1)
は
(x−a)2+(y−b)2=r2 …(2)
に変形できるとき，点 (a,b) を中心とする半径 r の円を表す．

（解説）
○簡単な例
　円の方程式 (x−2)2+(y−3)2=42 を展開すると
　x2−4x+4+y2−6y+9=16 となり，定数項をまとめると
　x2+y2−4x−6y−3=0 になる．

○　一般に，
　(x−a)2+(y−b)2=r2 …(2) の形の円の方程式は必ず
　x2+y2+Ax+By+C=0 …(1) の形に変形できる．

○　逆に，
　x2+y2+Ax+By+C=0 …(1) の形の方程式は，「平方完成」により，次のように変形できる．
　(x2+Ax)+(y2+By)=−C
　{x2+Ax+( )2}+{y2+By+( )2)=−C+( )2+( )2
　(x+ )2+(y+ )2= …(3) と変形できるから
右辺が正の数になるときは円を表す．
　右辺が負または０になる場合には，(1)は円を表さない．（右辺が0ならば単なる「点」となり，右辺が負ならば座標平面上に図示できない．）
［なぜ「･･･に変形できるとき」などと中途半端な言い方をするのか？］［なぜ，円を表すと言い切らないのか？］
　(2)は必ず(1)になる．
　しかし，(1)の多くは(2)に変形できるが，例外的にそうはならないものがあるので，このように言わざるを得ない．

例　(1)→(2)になり，円を表すもの
x2+y2+2x−4y−4=0
は
x2+2x+y2−4y=4
(x2+2x+1)+(y2−4y+4)=4+1+4
(x+1)2+(y−2)2=9
のように変形できるから，点 (−1,2) を中心とする半径 3 の円を表す．

例　(1)が円を表さないもの
x2+y2+2x−4y+6=0
は
x2+2x+y2−4y=−6
(x2+2x+1)+(y2−4y+4)=−6+1+4
(x+1)2+(y−2)2=−1 になり，
右辺が負の数になるので，r2=−1 からは半径が求まらない．したがって，このような円は描けない．
例　(1)が円を表さないもの
x2+y2+2x−4y+5=0
は
x2+2x+y2−4y=−5
(x2+2x+1)+(y2−4y+4)=−5+1+4
(x+1)2+(y−2)2=0 になり，
これが成立するのは，x=−1, y=2の場合だけだから，点(−1, 2)を表す．
　円を表すかどうかは「平方完成」の変形をやってみれば分かる．
■　平方完成は次のように行う
y も同様
例
_____x2+2x=(x+1)2−1
_____x2+4x=(x+2)2−4
_____x2+6x=(x+3)2−9

※　x2−2ax+a2=(x−a)2 だから x2−2ax=(x−a)2 - a2
⇒ - a2の符号に注意して以下の変形を見ること
_____x2−2x=(x−1)2−1　← 引き算のときも，マイナスになる
_____x2−4x=(x−2)2−4
_____x2−2x=(x−1)2−1　← 引き算のときも，マイナスになる

_____x2+x=(x+)2−　← １の半分は
_____x2−3x=(x−)2−　← 3の半分は
【例題】　次の方程式はどのような図形を表すか．
(1)　x2+y2−6x+10y+18=0

（答案）
　(x2−6x)+(y2+10y)=−18
　　(x2−6x+9)+(y2+10y+25)=−18+9+25
　　(x−3)2+(y+5)2=16
と変形できるから，点 (3 ,−5) を中心とする半径 4 の円を表す．
(2)　x2+y2+5x=0

（答案）
　(x2+5x)+y2=0
　　(x2+5x+)+y2=
　　(x+)2+y2=( )2
と変形できるから，点 (−, 0) を中心とする半径 の円を表す．

【問題２】　次の方程式が表す図形を求めなさい．（選択肢の中から正しいものをクリック）
(1)
x2+y2−2x+4y−4=0

(2)
x2+y2−6x+5=0

(3)
x2+y2+2y−2=0

(4)
x2+y2−4x+8y+17=0

(5)
x2+y2+5x+4=0

(6)
x2+y2+y=0

...（携帯版）メニューに戻る

...メニューに戻る

■［個別の頁からの質問に対する回答］[円の方程式について／18.7.13］
わかりやすい解説もついていて、途中式も丁寧に書かれてるので理解しやすかった。
＝＞［作者］：連絡ありがとう．
■［個別の頁からの質問に対する回答］[円の方程式について／18.6.12］
問題1(3)の解答解説が(2)のものになっています
＝＞［作者］：連絡ありがとう．訂正しました
■［個別の頁からの質問に対する回答］[円の方程式について／18.4.10］
工具顕微鏡や3次元測定器など各工場で一般的にかつ便利に使用してます。そもそも円の直径や座標が簡単に算出できる元はこの円の方程式があるからだと思い、基本に立ち返って勉強しました。たいへん参考になりました。ありがとうございます。
＝＞［作者］：連絡ありがとう．
■［個別の頁からの質問に対する回答］[円の方程式について／18.2.4］
体調不良などで授業を受けられなかったときに、教科書だけでは理解できないので利用させていただいております。解説、まとめられた公式とそこに至る証明、練習問題等あらゆる面で非常に助かっております。ありがとうございます。
＝＞［作者］：連絡ありがとう．
■［個別の頁からの質問に対する回答］[円の方程式について／17.11.27］
中学生です。今ちょうど2乗に比例の式をやっている３年生ですが、高校見学に行った際、数学の授業でグラフに円が書いてあって『何これ面白そう』と思い“円 グラフ 式”と検索し調べていました。他のサイトはどこも高校生向けというか、難しく中学生の私にはわかりませんでした。 しかしここのサイトは中学生でもできるように基本的な平方完成の仕方やルートの計算などこれでもか！とくらいにわかりやすく、円についてよく分かることが出来ました。 作られた問題は全て満点でとても気持ちが良かったです。 高校の数学もそんなに難しくないですね！！
＝＞［作者］：連絡ありがとう．
■［個別の頁からの質問に対する回答］[ 円の方程式について／17.10.29］
ありがとう
＝＞［作者］：連絡ありがとう．
■［個別の頁からの質問に対する回答］[円の方程式について／16.12.18］
国家試験の勉強で活用しましたが、大変懐かしく、解りやすく勉強させて頂きました。有難うございます。
＝＞［作者］：連絡ありがとう．