 ...（携帯版）メニューに戻る...(ＰＣ版)メニューに戻る*** 科目 *** 数Ⅰ・Ａ数Ⅱ・Ｂ数Ⅲ高卒・大学初年度 *** 単元 *** 式と証明点と直線円軌跡と領域三角関数 指数関数対数関数微分不定積分定積分 高次方程式数列漸化式と数学的帰納法 平面ベクトル空間ベクトル確率分布 ※高校数学Ⅱの「式と証明」について，このサイトには次の教材があります．
この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は，他の頁を見てください． が現在地です． ...（携帯版）メニューに戻る...(ＰＣ版)メニューに戻る↓多項式の割り算 ↓割り算の原理 ↓複雑な無理数の代入  ↓分数式の約分 ↓分数式の和差 ↓繁分数式 ↓オイラーの分数式・繁分数式 ↓恒等式 ↓等式の証明 ↓不等式の証明 ↓絶対不等式 ↓相加平均・相乗平均 ２乗比較 |
|
（準備）
【例】
▼この式の両辺を２乗してしまうと
となって， |
| ○ (移項する)→ (両辺を２乗する)→
【要点】
【類題】
（解答）これは，２次方程式 |
|
（式の値：複雑な無理数の代入）
【例】
この問題において，このような問題においては，この頁の先頭の例で示したように， （答案例） ｘ＝２＋√3 のとき，ｘ２－４ｘ＋１＝０・・・(1)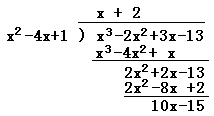 
ｘ３－２ｘ２＋３ｘ－１３ ＝（ｘ２－４ｘ＋１）（ｘ＋２）＋１０ｘ－１５・・・(2)だから ｘ３－２ｘ２＋３ｘ－１３ ＝１０ｘ－１５ ＝１０（２＋√3）－１５ ＝５＋１０√3・・・(答)
（参考）
＜１次式＞ ＜定数＝０次式＞ ｘ のかわりに ２＋√3 を代入すると，次数が１次下がります． ＜２次式＞ ＜定数＝０次式＞ ｘ２－４ｘ＋１ に ０ を代入すると，次数を一度に下げることができます． なお，ｘ２＝４ｘ－１ となるので， ＜２次式＞ ＜１次式＞ ｘ２ のかわりに ４ｘ－１ を代入すると，次数は１次だけ下がります．
ｘ＝２＋√3・・・(1)
ｘ２＝４ｘ－１・・・(2) を繰り返し適用すると，何次式でも１次または定数まで下げることができます． ｘ３＝ｘ・ｘ２＝ｘ（４ｘ－１） ＝４ｘ２－ｘ ＝４（４ｘ－１）－ｘ＝１５ｘ－４ ｘ４＝ｘ・ｘ３＝ｘ（１５ｘ－４）
ｘ３－２ｘ２＋３ｘ－１３
（よくある質問）
ｘ２－４ｘ＋１＝０ なのに，ｘ２－４ｘ＋１ で割るのは０で割ることにならないのか？ （回答）
|
| 【要点】
複雑な無理数を，次数の高い式に代入するには
【例】
（作業の手順）ｘ＝２＋√3 のとき， ｘ３－２ｘ２＋３ｘ－１３ の値を求めなさい．
(例)
(1) √ｎだけを右辺に残す．
ｘ－２＝√3
(2) ２乗する．
ｘ２－４ｘ＋４＝３
(3) ＝０ の形の方程式にする．
ｘ２－４ｘ＋１＝０
(4) 求める式を，方程式の左辺で割る．
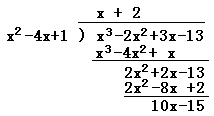
ｘ３－２ｘ２＋３ｘ－１３
(6) ｘの値は，余りに代入する．
＝（ｘ２－４ｘ＋１）（ｘ＋２）＋１０ｘ－１５ ＝１０ｘ－１５ （なぜなら，ｘ２－４ｘ＋１＝０） （次数を下げてから代入するところがポイント）
１０ｘ－１５
※ どうしても，単純に代入する方に魅力を感じる人へ：
＝１０（２＋√3）－１５ ＝５＋１０√3 以上に紹介した方法は，単に計算を楽にするだけのものでなく，この方法により「様々な問題に対する応用の道が開けてくる」と考えてください． |
|
...（携帯版）メニューに戻る...メニューに戻る
|
| ■このサイト内のGoogle検索■ |