|
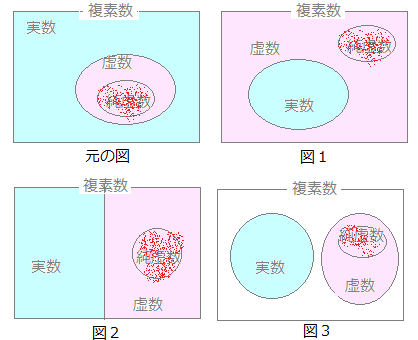
■中学校では扱わない2次方程式
■複素数とは(負の数の平方根と虚数・複素数)次のような2次方程式は中学校では扱わない。 (1) x2+2=0 …(1) (1)はx2=−2 と変形できるから、2乗が−2となる数が必要となる。 (2) x2−2x+5=0 (2)は(x−1)2=−4 と変形できるから、2乗が−4となる数が必要となる。 (3) 一般に、ax2+bx+c=0 (a≠0)の形でa , b , cの値を不用意に指定したとき、例えば 2x2+12x+23=0
は
2(x2+6x)+23=0
すなわち
2(x+3)2=−5
になり、その解を示すには2乗が負となる数を必要とするので、中学校で扱う数の範囲(実数の範囲)に解はない。
中学校ではx2=−1のような2次方程式の解は考えない
中学校で扱う数は実数と呼ばれ、数直線上に表示されるもので、2乗すれば必ず0以上になる。このため、中学校で扱う数の範囲ではx2の値が「負の数」となるようなものはない。
高校の数学IIではx2+1=0 すなわち x2=−1 …(1) のような2次方程式、さらに a(x−p)2+q=0 すなわち a(x−p)2=−q …(2) のような2次方程式、一般に任意の実数a , b , cに対して2次方程式 ax2+bx+c=0 (a≠0) …(3) の解を考えるために「負の数の平方根」「虚数」を導入する。 |
|
■虚数単位iの導入 根号を用いて2次方程式を解くには、x2=a ⇒ x=±という変形を行う。 これによりx2=−1を解くと、x=±のように根号の中が負である数が登場する。 同様にして、x2=−2 ⇒ x=± x2=−3 ⇒ x=± となるが、「負の数の平方根」を表す記号を1つずつ作らなくても1つだけi=と定めると、他の負の数の平方根はすべてこのiで表すことができる。 |
|
■虚数単位i=を定義すると、負の数の平方根はすべてこの虚数単位で表すことができる。
(1) −=−i
(2) ===i (3) ===i (4) ===2i (5) ===i (6) ===i |
|
【虚数単位iの定義】
さらに、x2−2x+5=0すなわち(x−1)2=−4のような2次方程式についてもx2=−1の1つの解を虚数単位といい、iで表す。 すなわち i= …(1) i2=−1 …(2) x−1=± x−1=±2i x=1±2i 一般に2次方程式を解くと、 (x−p)2=−q ⇒ x−p=± x=p± の形の数が登場する。(p , qは実数) そこでa+bi (a , bは実数)の形の数を考えれば、すべての2次方程式の解を表すことができる。このa+bi (a , bは実数)の形の数を複素数といい、aを実部、bを虚部という。 |
|
【複素数の定義】
a+bi (a , bは実数)の形の数を複素数といい、aを実部、bを虚部という。(2つの要素から成り立っている数・・・複素数) 複素数のうちで、特にb=0のものを実数という。 例 5+0iすなわち5は実数 これに対してb≠0のものを虚数という。 例 5−3iは虚数 複素数のうちで、特にa=0のものを純虚数という。 例 0+3iすなわち3iは純虚数 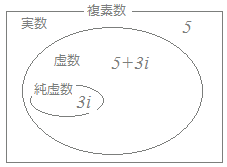
※a+biのa, bのうちで,ない方(=0の方)は書かずに省略するのが普通
虚部が0のもの,例えば5+0iは単に5と書く. 実部が0のもの,例えば0+5iは単に5iと書く. これに対して,実部も虚部も両方とも0のもの,すなわち0+0iは単に0と書く.(0iは0なのでけんかにならない⇒図参照)  それでいいのだ~♪
|
|
【複素数の計算規則】
虚数単位iを含む式の和差積商については、次の計算規則に従って計算する。 ○ iを含む式は、通常の文字式におけるa, b , c, x, yなどと同じように同類項の係数をまとめたり、和差積商の計算を行ったりすることができる。 (これだけでは、虚数単位の定義はどこへ行ったのか?と疑問を持つ人がいるかもしれないが、iについては通常の文字と異なる次の規則を追加する) ○ i2が登場すれば、−1に置き換える。 |
||||||||||||
例
|
|
例 (1+2i)+(3+4i)=4+6i (1+2i)−(5+7i)=−4−5i (1+2i)(1−3i)=1−i−6i2=1−i+6=7−i |
|
i8=i2·i2·i2·i2=(−1)(−1)(−1)(−1)=1 i33=(i2)16i=(−1)16i=i = = =−i ※ iを含む式は、最終的にa+bi (a, bは実数)の形になるように変形する (学習の記録用)■読み終わったら→ ここ ←をクリック■ |