← PC�p�͕ʕ�
|
← PC�p�͕ʕ�
�y���̋Ɍ��l�z �@ �� f(x) �ɂ����āCx �� a �ƈقȂ�l���Ƃ�Ȃ������Ȃ� a �ɋ߂Â��Ƃ��Cf(x) �� ���̒l b �Ɍ���Ȃ��߂Â��ꍇ�C f(x) = b �Ə����Cx �� a �Ɍ���Ȃ��߂Â��Ƃ��� f(x) �̋Ɍ��l�� b �ł���Ƃ����܂��B �@x �� a �����傫�Ȓl���Ƃ�Ȃ��� a �ɋ߂Â��Ƃ��ƁCa ���������Ȓl���Ƃ�Ȃ��� a �ɋ߂Â��̂���ʂ���Ƃ��́C �e�X
�@a+0��a−0��a�Ɠ����łȂ��̂��H�ȂǂƏ����w���̏펯�Łu�v�Z���Ă��܂��āv�͂����Ȃ��D
f(x)�@����+0��−0�́u�߂Â�����\���L���v�ɂȂ��Ă���D f(x) �ŕ\�킵�܂��B���E�ǂ��炩��߂Â��������߂Ȃ��Ƃ��C f(x) �ŕ\�킵�܂��B �@���ɁCx �� 0 �����傫�Ȓl���Ƃ�Ȃ���C0 �ɋ߂Â��Ƃ��� f(x) 0 ���������Ȓl���Ƃ�Ȃ���C0 �ɋ߂Â��Ƃ��� f(x) �ŕ\�킵�܂��B |
||||||||||||||||||||||||||||||||||||||||||||||||||||
|
�y�ȒP�ȋɌ��l�z ���@�������i�����j�̋Ɍ��l�́C���l�i�P�ɒl�����������́j�Ɠ������Ȃ�܂��B (2x + 1) = 3 (3x2 + 1) = 4 ���@���̐}�� y= �̃O���t�ł��B 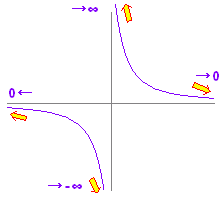 ���̐}����C���̂��Ƃ�������܂��B
## �悭����ԈႢ�̗� ## = 0 = �� �ˁ@����Șb�����Ă���̂ł͂Ȃ����Ƃɓ��ɒ��� = −�� …(1)×(-5) = −�� …(2)×3 = 0 …(3)×(-2) = 0 …(4)×6
�����w�����Ƃ������k�̏ꍇ�C��̉E���Ɏ������悤�ȊԈႢ���悭����܂��D���w�̐��Ƃł��M���V���ȗ�1000�N�ȏ���u�����v��u�Ɍ��v�̎�舵���ɂ͎肱�����Ă����̂ŁC�������Ȃ��b�ł��D
�@�u�����v��u�Ɍ��v�����܂�������悤�ɂȂ����̂́C�����Ȃ�u�����v��u�Ɍ��v���l�����ɁC�L���̊Ԃɏ��������߂Ă��܂��悤�ɂȂ��Ă���Ƃ�������ł��傤�D �@���Z�ł͓�������_�@�ɐ[���肹���ɁC�����I�ɗ�������悤�ɂȂ��Ă��܂��̂ŁC���̂悤�ɁC3���x�́u�����Ȏ����v�ōs�����\�z����Ƃ��ł��傤�D �@���̂悤��,�u�����v�ɂ��Ă̘b�́u���ׂėL���̘b�̒��Ō���Ă���v�ƍl����̂��R�c�ł��D …(1)�̏ꍇ
…(2)�̏ꍇ
…(3)�̏ꍇ
…(4)�̏ꍇ
|
|
������� ���s��`�̋Ɍ��� �@�s��`�̋Ɍ��Ƃ����p��́C���Z�̐�II�̋��ȏ��ł͎g���Ă��܂��C���ƁC���W�C�Q�l���ł͂悭�g���܂��B�s��`�̋Ɍ��ɂ��ďd�v�Ȃ��Ƃ́A�Ɍ����s��Ȃ̂ł͂Ȃ��āA�������������s�肾�ƌ������Ƃł��B �@��II�œo�ꂷ��s��`�̋Ɍ��́C����ƕ��q�̗����� 0 �ɋ߂Â��ꍇ�C���Ȃ킿�u��������v�@�@�ɂȂ��Ă�����̂������܂��B �i��III�ł́C���ɂ���-���ȂǑ����̌^���o�ꂵ�܂����C��II�ł́C�@�@�����ł��B�j �@�s��`�̋Ɍ������߂�ɂ́C����C���q�� 0 �ɂȂ錴�����u�ɂ���āv��菜���Ă���C�v�Z���܂��B
���@���ꁨ0�C���q��0�Ƃ����`�́u�s��`�̋Ɍ��v�ł́C����ƕ��q�������������āC������0�ɂȂ�Ƃ����������C�u���v�ɂ���Ď�菜���Ă���C�Ɍ��l�����߂܂��B
�@��@f’(a) = = = 2(x + a) = 4a �@��@f’(a) = = = (4a + 2h) = 4a |
|
|
|
���m�ʂ̕ł���̎���ɑ���n[�Ɍ��l�C�s��`�̋Ɍ��ɂ��ā^17.7.8�n
���ɂ��ĉ����A���������Ȃ��Alim�@�������@cos(n��/�Q)�@�̋Ɍ��ׂ�B
�Fn=1,2,3,4�E�E�E�Ƃ���A0,-1,0,1�E�E�E������U������B�Ƃ���܂���
n�͎��R���Ƃ͌���Ȃ���ŁA���������������͂܂����Ȃ��̂ł����H
�����m��ҁn�F�A�����肪�Ƃ��D
(1)�@���̕ł�S�����܂����������������e�͂ǂ��ɂ������Ă���܂���D�ǂ������̃T�C�g�⑼�̎Q�l���ɏ�����Ă����L�q�ɂ��āC���T�C�g�̊Ǘ��l�ɋ����q�ׂĂ�����̂ł�����u�]�˂̓G��Łv�̗ނŁC������͎���悭������܂���̂œ����ɂ����ł��D
(2)�@���e�I�ɂ́C���p����Ă��镶�͂��������u���Ȃ��̑S�ʔs�k�v�u���ނ̑S�ʏ����v�ł��D ���Ȃ킿�C������������������Ȃ� ����������ꍇ�ɂ́u�ǂ̂悤�ȋ߂Â��������Ă�����̒l�ɋ߂Â��v�ƌ����Ȃ���Ȃ���Ȃ�܂��C�u����߂Â�����������C�ǂ��܂ōs���Ă��قȂ�l�����v�ƌ�����C���̔ے�ɂȂ�܂��D (2.1) �Fn=1,2,3,4�E�E�E�Ƃ���A0,-1,0,1�E�E�E������U������B �ł���낵���� (2.2) n=1,3,5�E�E�E�Ƃ���A1,-1,1�E�E�E������U������B�Ƃ��Ă��ؖ��ɂȂ�܂��D (2.3) ���̎����l�ɂ������C (2.1)(2.2)�̓��Ă̕������}�����ł��傤�D �i�v����ɁC����߂Â����������Ƃ��ɁC����̒l�Ɏ��������C�U�������������Ώ\���Ȃ̂ŁC�Ȃ�ׂ��P���ȗ�������悢���ƂɂȂ�܂��j ���̂悤�ɁC�u�������Ȃ����Ƃ̏ؖ��͎������Ȃ��߂Â������̗���P�����悢�v���ƂɂȂ�܂��D |