数列の極限（∞／∞型）

...(ＰＣ版)メニューに戻る
*** 科目 ***
数Ⅰ・Ａ数Ⅱ・Ｂ数Ⅲ 高卒・大学初年度
*** 単元 ***
複素数平面二次曲線媒介変数表示と極座標
数列の極限関数導関数不定積分定積分
行列 1次変換

※高校数学Ⅲの「数列の極限」について，このサイトには次の教材があります．
この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は，他の頁を見てください．　が現在地です．

↓数列の極限（∞/∞型）-現在地
↓無理式の極限
↓rⁿの極限
↓同(2)
↓漸化式と極限

↓無限級数
循環小数

== 数列の極限(∞／∞型) ==

【はじめに】
○高校の教科書では，「数列の極限」を先に学習し，その後しばらくしてから「関数の極限」を学習するように教材が並んでいます．
○関数の極限では

lim_{x \to \infty} \frac{2 x + 1}{x - 1}

，

lim_{x \to - \infty} \frac{2 x + 1}{x - 1}

や

lim_{x \to 1} \frac{2 x + 1}{x - 1}

のように

lim_{x \to a} f (x)

において変数

x

が限りなく近づく値

a

は，
「

\infty

」も「

- \infty

」も「有限の値」もあります．

○これに対して，数列の極限では

lim_{n \to \infty} \frac{2 n + 1}{n - 1}

のように

lim_{n \to \infty} a_{n}

において第n項のnが近づく値としては「

\infty

」だけを考えます．「

- \infty

」や「有限の値」ということはありません．

※高校の数列は

a_{1}, a_{2}, a_{3}, \dots

のように正の整数番目の項だけを考えるので，

n \to - \infty

は考えないのは当然でしょう．
また，nは整数しかないので

n \to 1.5

ということもないでしょう．nが有限の正の整数（例えば5）の場合は，「近づく」必要はなく単純にその項（例えば

a_{5}

）を考えれば済むことなので，nが有限の値に「近づく」ということもありません．

数列の極限と言えば，

n \to \infty

の場合，すなわち

lim_{n \to \infty} a_{n}

，

lim_{n \to \infty} b_{n}

など無限数列で項の番号nが限りなく大きくなる場合のことです．

【収束するとは】
　nを限りなく大きくすると，anの値が限りなくある値αに近づいていくとき，数列 {an} はαに収束するといい

lim_{n \to \infty} a_{n} = α

で表す．このときαを数列 {an} の極限値という．

【例１】

lim_{n \to \infty} \frac{1}{n} = 0

…（重要）
【例２】

lim_{n \to \infty} (1 - \frac{3}{n}) = 1

高校の数学では，「限りなく近づく」とはどういうことかということを厳密には証明せず，直感的に理解するものとします．

(1)　nが10, 100, 1000, ...と限りなく大きくなるとき，

\frac{1}{n} = \frac{1}{10}, \frac{1}{100}, \frac{1}{1000}, . . .

= 0.1, 0.01, 0.001, . . .

のように，

\frac{1}{n}

は「限りなく０に近づきます」．
これが【例１】の意味です．この式は今後何度も登場しますので確実に答えられるようにしておきましょう．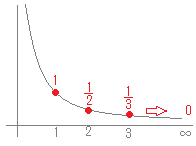

(2)　nが10, 100, 1000, ...と限りなく大きくなるとき，

\frac{3}{n} = \frac{3}{10}, \frac{3}{100}, \frac{3}{1000}, . . .

= 0.3, 0.03, 0.003, . . .

のように，

\frac{3}{n}

も「限りなく０に近づきます」．
だから，

lim_{n \to \infty} (1 - \frac{3}{n}) = 1 - 0 = 1

になります．【例２】
この極限は，上で示した（重要）を使えば

lim_{n \to \infty} (1 - \frac{3}{n}) = lim_{n \to \infty} (1 - 3 \times \frac{1}{n})

= 1 - 3 \times 0 = 1

とすることもできます．

【無限大とは】
　数列 {an} が「有限確定」の値に収束しないときは発散するといいます．

　正の無限大

\infty

は特定の数字ではありませんが，正の無限大に発散するときも極限があるといいます．
　負の無限大

- \infty

に発散するときも同様に，極限があるといいます．

　有限の値でなく「無限大に発散する」場合
【例３】

lim_{n \to \infty} (n + 1) = \infty

【例４】

lim_{n \to \infty} (- 3 n^{2}) = - \infty

　高校の数学では，「無限大」とは何かということを厳密には定義せず，直感的に理解するものとします．
　

\infty

というのは特定の値を表す（１つの）数字ではないので，普通の文字式のように扱うことはできません．

lim_{n \to \infty} n = \infty

だからといって，

lim_{n \to \infty} (n + 1) = \infty + 1

とは書きません．
また，

lim_{n \to \infty} (n + 1)

は"無限よりも大きい"とは言いません．
さらに，

\infty + 1 = \infty

なら

1 = 0

かとも考えません．

　nが10, 100, 1000, ...と限りなく大きくなるとき，n+1も限りなく大きくなるということを，単に

lim_{n \to \infty} (n + 1) = \infty

と書きます．【例３】

　高校の数学では，無限大の厳密な定義（εδ論法）を要求しませんので

lim_{n \to \infty} (n + 1) = \infty

を証明せよとは言いません．

n < n + 1

であって，かつ

n \to \infty

だから

n + 1 \to \infty

とするまでです．

　同様にして，無限大になる式の定数倍も無限大と書きます．

lim_{n \to \infty} 2 n = \infty

　ただし，符号が逆の場合は負の無限大になります．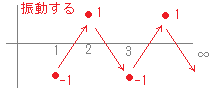

lim_{n \to \infty} (- 2 n) = - \infty

lim_{n \to \infty} (- 3 n^{2}) = - \infty

【例４】

　有限ではあっても「振動して値が確定しない」場合も，数列は発散するといいます．
【例５】

lim_{n \to \infty} (- 1)^{n}

…（極限なし，発散）

　絶対値が無限に大きくなってかつ振動する場合も発散です．
【例６】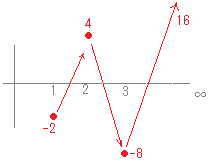

lim_{n \to \infty} (- 2)^{n}

…（極限なし，発散）

　振動する場合でも振幅が０に近づく場合は収束します．
【例７】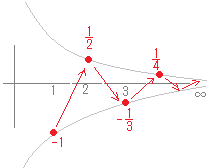

lim_{n \to \infty} \frac{(- 1)^{n}}{n} = 0

【ここまでの要約】
【例１，２】　有限確定の極限値に収束するもの

lim_{n \to \infty} \frac{1}{n} = 0

lim_{n \to \infty} (1 - \frac{3}{n}) = 1

【例３】　正の無限大に発散するもの

lim_{n \to \infty} (n + 1) = \infty

【例４】　負の無限大に発散するもの

lim_{n \to \infty} (- 3 n^{2}) = - \infty

【例５】　有限であるが振動するもの

lim_{n \to \infty} (- 1)^{n}

…（極限なし）
【例６】　絶対値が無限に大きくなって振動するもの

lim_{n \to \infty} (- 2)^{n}

…（極限なし）
【例７】　振動するが振幅が０に近づいて収束するもの

lim_{n \to \infty} \frac{(- 1)^{n}}{n} = 0

【問題１】
　下の選択肢のうちで正しいものをクリックしてください．

(1)　一般項が次の式で表される数列の極限を求めてください．

a_{n} = 2 n + 3

- \infty

2

3

5

\infty

解説やり直す

数列 {

a_{n}

} の極限とは，

lim_{n \to \infty} a_{n}

のことです

lim_{n \to \infty} (2 n + 3) = \infty

nが限りなく大きくなるとき，2n (>n)も2n+3 (>2n>n)も限りなく大きくなる

(2)　一般項が次の式で表される数列の極限を求めてください．

2 + \frac{3}{n}

2

3

5

6

\infty

解説やり直す

数列 {

2 + \frac{3}{n}

} の極限とは，

lim_{n \to \infty} (2 + \frac{3}{n})

のことです

\frac{3}{n} \to 0

だから

lim_{n \to \infty} (2 + \frac{3}{n}) = 2

(3)　次の極限を求めてください．

lim_{n \to \infty} (- 3 n^{2})

- \infty

- 9

- 6

9

\infty

解説やり直す

n \to \infty

のとき

n^{2} \to \infty

だから

lim_{n \to \infty} (- 3 n^{2}) = - \infty

(4)　次の極限を求めてください．

lim_{n \to \infty} (- 1)^{n + 1}

- \infty

- 1

0

1

\infty

なし

解説やり直す

n=1, 2, 3, 4, ...と増えていくとき
1, −1, 1, −1, 1, ...と振動するから
極限なし

(5)　次の極限を求めてください．

lim_{n \to \infty} (- 2^{n})

- \infty

- 2

0

2

\infty

なし

解説やり直す

2^{n} \to \infty

だから

lim_{n \to \infty} (- 2^{n}) = - \infty

(6)　次の極限を求めてください．

lim_{n \to \infty} (- \frac{1}{2})^{n}

- \infty

- \frac{1}{2}

0

\frac{1}{2}

\infty

なし

解説やり直す

n=1, 2, 3, 4, ...と増えていくとき

- \frac{1}{2}, \frac{1}{4}, - \frac{1}{8}, \frac{1}{16}, . . .

と絶対値が限りなく０に近づくから，振動していても極限値がある．

lim_{n \to \infty} (- \frac{1}{2})^{n} = 0

【ここから後の要約】
(1)　多項式形の数列の極限
【変形】　次数が最大の項でくくる（→解説１）

lim_{n \to \infty} (3 n^{2} - 4 n) = lim_{n \to \infty} 3 n^{2} (1 - \frac{4 n}{3 n^{2}})

lim_{n \to \infty} (- 2 n^{2} + 3 n) = lim_{n \to \infty} (- 2 n^{2}) (1 - \frac{3 n}{2 n^{2}})

【結果】　次数が最大の項だけで決まり，次数の低い項は影響しない（→解説２）

lim_{n \to \infty} 3 n^{2} (1 - \frac{4}{3 n}) = \infty

lim_{n \to \infty} (- 2 n^{2}) (1 - \frac{3}{2 n}) = - \infty

(2)　分数式形の数列の極限
【変形】　分母と分子の各々を次数最大の項でくくる（→解説３）

lim_{n \to \infty} \frac{2 n - 1}{n + 1} = lim_{n \to \infty} \frac{2 n (1 - \frac{1}{2 n})}{n (1 + \frac{1}{n})}

【結果】　次数が最大の項だけで決まり，次数の低い項は影響しない
（分母の次数）＞（分子の次数）なら「0」になる（→解説４）

lim_{n \to \infty} \frac{2 n - 1}{n^{2} + 1} = lim_{n \to \infty} \frac{2 n (1 - \frac{1}{2 n})}{n^{2} (1 + \frac{1}{n^{2}})}

= lim_{n \to \infty} \frac{2 (1 - \frac{1}{2 n})}{n (1 + \frac{1}{n^{2}})}

= lim_{n \to \infty} \frac{2}{n} = 0

（分母の次数）＝（分子の次数）なら「次数最大の項の係数の比」になる（→解説５）

lim_{n \to \infty} \frac{2 n - 1}{n + 1} = lim_{n \to \infty} \frac{2 n (1 - \frac{1}{2 n})}{n (1 + \frac{1}{n})}

= lim_{n \to \infty} \frac{2 (1 - \frac{1}{2 n})}{(1 + \frac{1}{n})}

= lim_{n \to \infty} \frac{2}{1} = 2

（分母の次数）＜（分子の次数）なら「∞または−∞」になる（→解説６）

lim_{n \to \infty} \frac{2 n^{2} - 1}{n + 1} = lim_{n \to \infty} \frac{2 n^{2} (1 - \frac{1}{2 n^{2}})}{n (1 + \frac{1}{n})}

= lim_{n \to \infty} \frac{2 n (1 - \frac{1}{2 n})}{(1 + \frac{1}{n})}

= lim_{n \to \infty} \frac{2 n}{1} = \infty

lim_{n \to \infty} \frac{- 2 n^{2} + 1}{3 n + 1} = lim_{n \to \infty} \frac{- 2 n^{2} (1 - \frac{1}{2 n^{2}})}{3 n (1 + \frac{1}{3 n})}

= lim_{n \to \infty} \frac{- 2 n (1 - \frac{1}{2 n^{2}})}{3 (1 + \frac{1}{3 n})}

= lim_{n \to \infty} \frac{- 2 n}{3} = - \infty

（解説１）
　多項式の形の数列の極限で

lim_{n \to \infty} (n^{2} + 4 n)

や

lim_{n \to \infty} (- 2 n^{2} - 3 n)

のように見かけ上「∞＋∞」や「−∞−∞」に見えるものの極限は，直ちに「∞」「−∞」と答えられます．
　これに対して，

lim_{n \to \infty} (3 n^{2} - 4 n)

のように「大きくするものと小さくするものが対立」しているとき，どちらが強いか決着をつける必要があります．

lim_{n \to \infty} (3 n^{2} - 4 n) = lim_{n \to \infty} 3 n^{2} (1 - \frac{4 n}{3 n^{2}})

= lim_{n \to \infty} 3 n^{2} (1 - \frac{4}{3 n})

のように次数最大の項でくくると，

1 - \frac{4}{3 n} \to 1

となるので，次数の低い項は結果に影響していないことが分かります．

（解説２）
　上の解説１のように変形すると，つねに

lim_{n \to \infty} (a n + b) = lim_{n \to \infty} a n

lim_{n \to \infty} (a n^{2} + b n + c) = lim_{n \to \infty} a n^{2}

lim_{n \to \infty} (a n^{3} + b n^{2} + c n + d) = lim_{n \to \infty} a n^{3}

となって，次数が最大の項だけを見れば結果が得られますが，いろいろな応用問題にも対応できるように「最大項でくくる」という変形方法も覚えておく方がよいでしょう．

（解説３）
　

lim_{n \to \infty} (n + 1) (2 n - 1)

のように見かけ上「∞×∞」に見えるものは直ちに「∞」と答えることができます．

　これに対して，

lim_{n \to \infty} \frac{2 n - 1}{n + 1}

のように

\frac{\infty}{\infty}

に見えるものは，分母（小さくするもの）が強いか分子（大きくするもの）が強いかの決着をつける必要があります．
　はじめに「分母と分子の各々を次数最大の項でくくり」，次に「最大項同士を約分すると」結果が見えます．

lim_{n \to \infty} \frac{2 n - 1}{n + 1} = lim_{n \to \infty} \frac{2 n (1 - \frac{1}{2 n})}{n (1 + \frac{1}{n})}

= lim_{n \to \infty} \frac{2 n}{n} \times \frac{(1 - \frac{1}{2 n})}{(1 + \frac{1}{n})}

= lim_{n \to \infty} \frac{2}{1} \times \frac{1}{1} = 2

とできます．

（解説４，５，６）
　上記の解説３のように「最大項でくくる」をキーワードに変形していくと，分母，分子とも次数の低い項は結果に影響せず

lim_{n \to \infty} \frac{a n + b}{p n^{2} + q n + r} = lim_{n \to \infty} \frac{a n}{p n^{2}} = lim_{n \to \infty} \frac{a}{p n}

lim_{n \to \infty} \frac{a n + b}{p n + q} = lim_{n \to \infty} \frac{a n}{p n} = lim_{n \to \infty} \frac{a}{p}

lim_{n \to \infty} \frac{a n^{2} + b + c}{p n + q} = lim_{n \to \infty} \frac{a n^{2}}{p n} = lim_{n \to \infty} \frac{a n}{p}

などと最大項と最大項の比になり，約分すれば結果が見えます．

【要点】
　多項式でも分数式でも，「次数最大の項でくくれば」なんとかなります．

【問題２】
　次の数列の極限を求めてください．（下の選択肢のうちで正しいものをクリック）

(1)

lim_{n \to \infty} (2 n - 3)

- \infty

- 6

- 1

1

\infty

なし

解説やり直す

次数が最大の項2nでくくると

lim_{n \to \infty} (2 n - 3) = lim_{n \to \infty} 2 n (1 - \frac{3}{2 n})

ここで

lim_{n \to \infty} 2 n = \infty, lim_{n \to \infty} (1 - \frac{3}{2 n}) = 1

だから

lim_{n \to \infty} 2 n (1 - \frac{3}{2 n}) = \infty

(2)

lim_{n \to \infty} (2 n - 3 n^{2})

- \infty

- 9

- 1

9

\infty

なし

解説やり直す

次数が最大の項−3n2でくくると

lim_{n \to \infty} (2 n - 3 n^{2}) = lim_{n \to \infty} (- 3 n^{2}) (- \frac{2}{3 n} + 1)

ここで

lim_{n \to \infty} (- 3 n^{2}) = - \infty, lim_{n \to \infty} (- \frac{2}{3 n} + 1) = 1

だから

lim_{n \to \infty} (- 3 n^{2}) (- \frac{2}{3 n} + 1) = - \infty

(3)

lim_{n \to \infty} \frac{3 n - 1}{2 n^{2} + 1}

- \infty

0

\frac{3}{2}

\infty

なし

解説やり直す

分母を次数最大の項2n2でくくり，分子を次数最大の項3nでくくると

lim_{n \to \infty} \frac{3 n - 1}{2 n^{2} + 1} = lim_{n \to \infty} \frac{3 n (1 - \frac{1}{3 n})}{2 n^{2} (1 + \frac{1}{2 n^{2}})}

= lim_{n \to \infty} \frac{3}{2 n} \times \frac{1 - \frac{1}{3 n}}{1 + \frac{1}{2 n^{2}}}

ここで

lim_{n \to \infty} \frac{3}{2 n} = 0

lim_{n \to \infty} (1 - \frac{1}{3 n}) = 1, lim_{n \to \infty} (1 + \frac{1}{2 n^{2}}) = 1

だから

lim_{n \to \infty} \frac{3 (1 - \frac{1}{3 n})}{2 n (1 + \frac{1}{2 n^{2}})} = 0

※分母の次数が分子の次数よりも高いとき，極限値は０になる．

(4)

lim_{n \to \infty} \frac{3 n + 1}{2 n - 1}

- \infty

0

\frac{3}{2}

\infty

なし

解説やり直す

分母を次数最大の項2nでくくり，分子を次数最大の項3nでくくると

lim_{n \to \infty} \frac{3 n + 1}{2 n - 1} = lim_{n \to \infty} \frac{3 n (1 + \frac{1}{3 n})}{2 n (1 - \frac{1}{2 n})}

= lim_{n \to \infty} \frac{3 (1 + \frac{1}{3 n})}{2 (1 - \frac{1}{2 n})}

ここで

lim_{n \to \infty} (1 + \frac{1}{3 n}) = 1, lim_{n \to \infty} (1 - \frac{1}{2 n}) = 1

だから

lim_{n \to \infty} \frac{3 (1 + \frac{1}{3 n})}{2 (1 - \frac{1}{2 n})} = \frac{3}{2}

※分母と分子の次数が等しいときは，極限値は最大項の係数の比になる．

(5)

lim_{n \to \infty} \frac{- 3 n^{2} + 1}{2 n - 1}

- \infty

- \frac{3}{2}

0

\infty

なし

解説やり直す

分母を次数最大の項2nでくくり，分子を次数最大の項−3n2でくくると

lim_{n \to \infty} \frac{- 3 n^{2} + 1}{2 n - 1} = lim_{n \to \infty} \frac{- 3 n^{2} (1 - \frac{1}{3 n^{2}})}{2 n (1 - \frac{1}{2 n})}

= lim_{n \to \infty} \frac{- 3 n}{2} \times \frac{1 - \frac{1}{3 n^{2}}}{1 - \frac{1}{2 n}}

ここで

\frac{- 3 n}{2} \to - \infty

lim_{n \to \infty} (1 - \frac{1}{3 n^{2}}) = 1, lim_{n \to \infty} (1 - \frac{1}{2 n}) = 1

だから

lim_{n \to \infty} \frac{- 3 n}{2} \times \frac{1 - \frac{1}{3 n^{2}}}{1 - \frac{1}{2 n}} = - \infty

※分子の次数が分母の次数よりも大きいとき，極限は正または負の無限大になる．

...（携帯版）メニューに戻る

...（PC版）メニューに戻る

髫ｨ�ｽ�ｿ�ｽ驍ｵ�ｺ髦ｮ蜻ｻ�ｿ�ｽ驛｢�ｧ�ｽ�ｵ驛｢�ｧ�ｽ�､驛｢譏懶ｽｺ�･�ｽ�ｽ驍ｵ�ｺ�ｽ�ｮGoogle髫ｶﾂ隲幢ｿｽ�ｽ�ｴ�ｽ�｢髫ｨ�ｽ�ｿ�ｽ

髫ｨ�ｽ�ｽ�ｳ驍ｵ�ｺ髦ｮ蜻ｻ�ｿ�ｽ驛｢譎擾ｽ｣�ｹ�ｽ�ｽ驛｢�ｧ�ｽ�ｸ驍ｵ�ｺ�ｽ�ｮ髯ｷ閧ｲ�｣�ｯ�ｽ�ｽ�ｽ�ｭ驍ｵ�ｺ�ｽ�ｫ髫ｰ魃会ｽｽ�ｻ驛｢�ｧ鬩ｫﾂ霎滂ｽ｡驍ｵ�ｲ�ｽ�ｽ驛｢�ｧ�ｽ�｢驛｢譎｢�ｽ�ｳ驛｢�ｧ�ｽ�ｱ驛｢譎｢�ｽ�ｼ驛｢譎会ｽ｣�ｯ�つ遶擾ｽｽ�ｽ�ｿ�ｽ�｡驍ｵ�ｲ�ｽ�ｽ
… 驍ｵ�ｺ髦ｮ蜻ｻ�ｿ�ｽ驛｢�ｧ�ｽ�｢驛｢譎｢�ｽ�ｳ驛｢�ｧ�ｽ�ｱ驛｢譎｢�ｽ�ｼ驛｢譎冗樟�ｽ�ｽ髫ｰ�ｨ陷ｻ蜿夜ｧ�垈�ｾ�ｽ�ｹ髯懈ｻゑｽｿ�ｽ�ｽ�ｽ髯ｷ�ｿ郢ｧ迺ｰﾂ�ｽ�ｽ遶企豪�ｸ�ｺ髴域喚髮ｷ驍ｵ�ｺ�ｽ�ｦ驍ｵ�ｺ�ｽ�ｽ隨ｳ�ｽ�ｸ�ｺ�ｽ�ｽ驍ｵ�ｺ鬮ｦ�ｪ遶擾ｽｪ驍ｵ�ｺ�ｽ�ｽ

髫ｨ�ｽ�ｿ�ｽ驍ｵ�ｺ髦ｮ蜻ｻ�ｿ�ｽ鬯ｯ�ｽ�ｽ遶企豪�ｸ�ｺ�ｽ�､驍ｵ�ｺ�ｽ�ｽ遯ｶ�ｻ�ｽ�ｽ霑ｹ螢ｽ�ｽ驍ｵ�ｺ�ｽ�ｽ陜ｨ謚ｵ�ｿ�ｽ隴ｴ�ｧ邵ｺ讙趣ｽｸ�ｺ�ｽ�ｽ陜ｨ謚ｵ�ｿ�ｽ驕停或�ｿ�｣鬯ｩ謌奇ｽｼ雋ｻ�ｼ讓抵ｽｸ�ｺ�ｽ�ｮ髫ｰ蜴�ｽｿ�ｽ鬩包ｽｭ�ｽ�ｽ陟募ｨｯ關ｽ驍ｵ�ｺ�ｽ�ｮ髣皮判縺假ｿｽ�ｽ髫ｲ�｢雋企ｳｶ�ｦ驍ｵ�ｺ陟募ｨｯ譌ｺ驛｢�ｧ陟暮ｯ会ｽｿ�ｽ鬯ｨ�ｾ遶擾ｽｽ�ｽ�ｿ�ｽ�｡驍ｵ�ｺ陷会ｽｱ遯ｶ�ｻ驍ｵ�ｺ闕ｳ蟯ｩ蜻ｳ驍ｵ�ｺ髴郁ｲｻ�ｼ讖ｸ�ｿ�ｽ�ｽ�ｽ

髫ｨ�ｳ陋ｹ�ｺ隴ｫ螟撰ｿｽ�ｽ�ｽ驍ｵ�ｺ�ｽ�ｮ髯溷私�ｽ�｢驛｢�ｧ陋幢ｽｵ�ｽ�ｽ驍ｵ�ｺ�ｽ�ｦ驍ｵ�ｺ�ｽ�ｽ�ｽ邇厄ｽｫ�｢雋企ｳｶ�ｦ驍ｵ�ｺ�ｽ�ｯ髯ｷ闌ｨ�ｽ�ｨ鬯ｩ蟷｢�ｽ�ｨ鬮ｫ�ｱ�ｽ�ｭ驍ｵ�ｺ�ｽ�ｾ驍ｵ�ｺ陝ｶ蜷ｮﾂ�ｻ驛｢�ｧ郢ｧ�ｽ�ｽ閾･�ｸ�ｺ�ｽ�｣驍ｵ�ｺ�ｽ�ｦ驍ｵ�ｺ�ｽ�ｽ遶擾ｽｪ驍ｵ�ｺ陷ｻ�ｻ�ｽ�ｼ�ｽ�ｽ
髫ｨ�ｳ陋ｹ�ｺ隨渉髫ｲ�ｽ�ｽ�ｳ驍ｵ�ｺ�ｽ�ｮ髯ｷﾂ�ｽ�ｽ邵ｲ謚ｵ�ｿ�ｽ陟募ｨｯ�ｽ驍ｵ�ｺ�ｽ�ｮ髯懶ｿｽ陜楢ｶ｣�ｽ�｡陟募ｨｯﾂ�ｲ驍ｵ�ｺ�ｽ�ｩ驍ｵ�ｺ�ｽ�ｽ邵ｲ蝣､�ｸ�ｺ郢ｧ�ｽ螟｢驍ｵ�ｺ雋�ｼ会ｽｰ驛｢�ｧ陷ｻ闌ｨ�ｽ�ｭ�ｽ�｣鬩墓慣�ｽ�ｺ驍ｵ�ｺ�ｽ�ｪ髫ｴ�ｽ�ｿ�ｽ�ｽ�ｫ�ｽ�ｽ驍ｵ�ｺ�ｽ�ｧ髣費ｽｨ隴擾ｽｴ遶擾ｽｴ驍ｵ�ｺ�ｽ�ｦ驍ｵ�ｺ�ｽ�ｽ隨ｳ�ｽ�ｸ�ｺ�ｽ�ｽ驍ｵ�ｺ�ｽ�ｽ隨ｳ�ｽ�ｬ�ｾ�ｽ�ｹ髯懈ｻゑｽｿ�ｽ�ｽ�ｦ遶擾ｽｵ隰泌調�ｸ�ｺ�ｽ�ｫ髯晢ｿｽ�ｽ�ｾ驍ｵ�ｺ陷会ｽｱ遯ｶ�ｻ驍ｵ�ｺ�ｽ�ｯ�ｽ�ｽ隰疲ｺｷ�ｺ�ｽ螯呻ｿｽ�ｽ驍ｵ�ｺ�ｽ�ｪ鬯ｮ�ｯ髣企ｯ会ｽｽ鬘俶ｱ橸ｿｽ�ｾ髯滂ｽ｢隲帛ｲｩ�ｽ驛｢�ｧ闕ｵ譎｢�ｽ閧ｲ�ｸ�ｺ�ｽ�ｽ遶企豪�ｸ�ｺ陷会ｽｱ遯ｶ�ｻ驍ｵ�ｺ�ｽ�ｽ遶擾ｽｪ驍ｵ�ｺ陷ｻ�ｻ�ｽ�ｼ髮懶ｽ｣�ｽ�ｼ鬩包ｽｺ�つ�ｽ�ｻ驍ｵ�ｺ�ｽ�ｪ驍ｵ�ｺ陞ゑｿｽ�ｽ�ｼ隴ｴ�ｧ陋ｻ�､髫ｰ�ｦ�ｽ�ｽ陜趣ｽｪ驍ｵ�ｺ�ｽ�ｪ髫ｴ�ｽ�ｿ�ｽ�ｽ�ｫ�ｽ�ｽ驍ｵ�ｺ�ｽ�ｫ驍ｵ�ｺ�ｽ�ｪ驍ｵ�ｺ�ｽ�｣驍ｵ�ｺ�ｽ�ｦ驍ｵ�ｺ�ｽ�ｽ�ｽ邇匁捗�ｽ�ｴ髯ｷ�ｷ陋ｹ�ｻ�ｽ�ｽ�ｽ�ｽ陟募ｨｯ關ｽ驛｢�ｧ陟暮ｯ会ｽｽ螳壽ｦ�ｽ�ｬ鬯ｮ�｢闕ｵ譏ｶ�ｽ驛｢�ｧ闕ｵ譏ｶ�ｽ鬩包ｽｲ�ｽ�ｽ�つ�ｽ�ｽ隨�ｽ｡驍ｵ�ｺ闔会ｽ｣邵ｲ蝣､�ｸ�ｺ�ｽ�ｪ驍ｵ�ｺ陷托ｽｰ�ｽ�ｪ�ｽ�ｭ鬮｢�ｽ�ｽ�ｽ�ｽ繧句擅�ｽ�ｭ驛｢�ｧ�つ驍ｵ�ｺ髦ｮ蜷ｮ�ｽ驍ｵ�ｺ�ｽ�ｫ驍ｵ�ｺ�ｽ�ｪ驛｢�ｧ驗呻ｽｫ遶擾ｽｪ驍ｵ�ｺ陷ｷ�ｶ�ｽ�ｽ驍ｵ�ｺ�ｽ�ｧ�ｽ�ｽ隴ｴ�ｧ雎撰ｽｻ鬨ｾ蛹�ｽｽ�ｨ驍ｵ�ｺ陷会ｽｱ遶擾ｽｪ驍ｵ�ｺ陝ｶ蜻ｻ�ｽ髮｣�ｿ�ｽ髮懶ｽ｣�ｽ�ｼ�ｽ�ｽ

鬮ｮ莨夲ｽｽ�ｪ髯懶ｿｽ闕ｳ蟯ｩ�ｽ髯晢ｿｽ�ｽ�ｾ驍ｵ�ｺ陷ｷ�ｶ�ｽ邇匁綜隶捺慣�ｽ�ｭ隴∵腸�ｿ�ｽ髣包ｽｳ�ｽ�ｭ髯晢ｿｽ�ｽ�ｦ髴大｣ｼ迴ｾ�ｽ�ｽ驍ｵ�ｺ髦ｮ蜻ｻ�ｿ�ｽ鬯ｯ�ｽ�ｿ�ｽ�ｽ�ｽ驕抵ｿｽ�ｽ�ｫ闖ｫ�ｶ�ｽ�ｽ�ｽ�｡髴大｣ｼ迴ｾ�ｽ�ｽ驍ｵ�ｺ髦ｮ蜻ｻ�ｿ�ｽ鬯ｯ�ｽ�ｿ�ｽ驍ｵ�ｺ�ｽ�ｫ驍ｵ�ｺ郢ｧ�ｽ�ｽ鬘費ｽｸ�ｺ�ｽ�ｾ驍ｵ�ｺ�ｽ�ｽ