← PC用は別頁

【　グラフの平行移動　】
【　グラフの平行移動　】　･･･(1)
　関数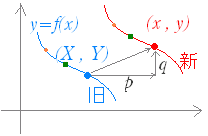
y=f(x)
のグラフを x 軸の正の向きに p， y 軸の正の向きに q だけ平行移動してできるグラフの方程式は
y=f(x−p)+q
になる．

例　y=f(x) のグラフを右に 2，上に 3 だけ平行移動すると，
y=f(x−2)+3
になる．
（解説）+ （灰色表示は舞台裏のささやき）
○ 　あるグラフ上の任意の点 (x , y) が満たす関係式 y=f(x) をこのグラフの方程式とする．
　グラフの移動と言っても，いきなりグラフ全体を移動すると考えると難しくなるので，古い点をそれぞれ移動させて，出来た新しい点をつないだものが新しいグラフだと考える．
○　移動前のグラフ（旧グラフ）上の点を (X , Y) ，移動後のグラフ（新グラフ）上の点を (x , y) とおくと，旧グラフ上の点 (X , Y) は y=f(x) 上にあるから，
Y=f(X) …(1)
が成り立つ．
　点 (X , Y) を x 軸の正の向きに（右に）p，y 軸の正の向きに（上に）q だけ平行移動したものが点 (x , y) だから
x=X+p …(2)
y=Y+q …(3)
が成り立つ．
　ここまでは，常識通り，右に移動するときは x 座標がプラスされ，上に移動するときは y 座標がプラスされている．

○　新しいグラフの方程式を求めるのだから，新座標 (x , y) が満たす関係式を求めればよい．
　そのためには，(2)(3)から旧座標 (X , Y) を(1)に代入消去すればよい．
X=x−p …(2’)
Y=y−q …(3’)
　これらを(1)に代入すると，
y−q=f(x−p) …(1’)
となってできあがり．
　通常よく使う y= の形にすれば， q を移項して
y=f(x−p)+q
になる．
　右に 2 移動するときに x+2 ではなくて，x - 2 になるのは我慢するとしても，x だけマイナスにされて y だけプラスになっているのは不公平じゃないのか？
　⇒　y−q=f(x−p) なので，右に 2 移動するときに x - 2 になって，上に 3 移動するときに y - 3 でつじつまが合っている．
○　公式をよく見てみると，手品でも何でもなくて

y−q=f(x−p)
のように，旧座標 (X , Y) の関係が書かれているだけであることが分かる．（透かしのように浮かび上がる）

○　新座標から旧座標を求めるには
X=x−p …(2’)
Y=y−q …(3’)
のように引き算になるというのが，引き算が登場する原因となっている．

具体例
(1)　１次関数
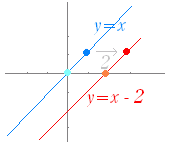
　直線 y=x のグラフを x 軸の正の向きに（右に） 2 だけ平行移動してできるグラフの方程式は
y=x−2
(2)　２次関数
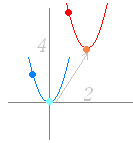
　放物線 y=3x2 のグラフを x 軸の正の向きに（右に） 2，y 軸の正の向きに（上に） 4 だけ平行移動してできるグラフの方程式は
y=3(x−2)2+4
(3)　分数関数
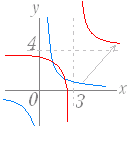
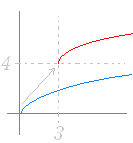
　直角双曲線 y= のグラフを x 軸の正の向きに（右に） 3，y 軸の正の向きに（上に） 4 だけ平行移動してできるグラフの方程式は
y=+4
(4)　無理関数
　y= のグラフを x 軸の正の向きに（右に） 3，y 軸の正の向きに（上に） 4 だけ平行移動してできるグラフの方程式は
y=+4
(5)　三角関数
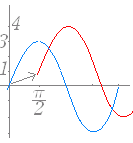
　y=3 sin x のグラフを x 軸の正の向きに（右に） ，y 軸の正の向きに（上に） 1 だけ平行移動してできるグラフの方程式は

y=3 sin(x−)+1
(6)　円
　円のグラフの方程式のように，y= ··· の形に（陽に）解いた形に書けないものは，右の(2)の形でグラフの移動を考える．
　x2+y2=r2 のグラフを x 軸の正の向きに（右に） p，y 軸の正の向きに（上に） q だけ平行移動してできるグラフの方程式は
(x−p)2+(y−q)2=r2
（余談）
　　数十年前に生徒から受けた質問：「公式には f があるのに，例題には f がない． f はどこに行ったのか？」
　⇒ f(x) というのは，関数に付けた名前で x のところに値を入れて使えるようになっている．
  • f(x)=x2 のとき，f(3)=32=9
  • f(x)=2x+3 のとき，f(1)=5
    　平行移動の公式では，次のような取り扱いに慣れることが重要．
  • f(x)=2x−1 のとき，f(a)=2a−1
  • f(x)=3x2 のとき，f(a+1)=3(a+1)2
  • f(x)=4x2 のとき，f(x−1)=4(x−1)2
【　グラフの平行移動　】　･･･(2)
f(x , y)=0
のグラフを x 軸の正の向きに p， y 軸の正の向きに q だけ平行移動してできるグラフの方程式は
f(x−p , y−q)=0
になる．



■読み終わったら→　ここ　←をクリック■

［注］直前にPC版から入られた場合は，自動転送でスマホ版に来ていますので，ブラウザの［戻るキー］では戻れません（堂々巡りになる）．下記のリンクを使ってメニューに戻ってください．
...（携帯版）メニューに戻る

...（PC版）メニューに戻る