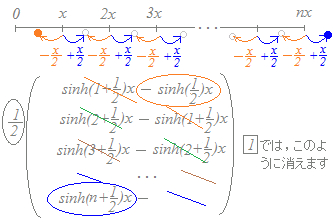|
I【双曲線関数の定義】
指数関数を使って次のように定義される関数を双曲線関数といいます. sinhx= …(1) coshx= …(2) tanhx= …(3)
◇覚え方◇
オイラーの公式から e ix=cosx+isinx , e −ix=cosx−isinx だから cosx=…(2') , sinx=…(1') 
II【双曲線関数の性質<相互関係>】
(解説)三角関数(円関数)と比較すると,全体的には似ていますが,少しだけ違う部分があります. まず,記号の約束として,(sinx)2, (cosx)2, (tanx)2のことを,各々sin2x , cos2x , tan2xなどと書くのと同様に,(sinhx)2, (coshx)2, (tanhx)2のことを,各々sinh2x , cos2x , tanh2xなどと書きます.
(4)← cosh2x−sinh2x=( )2−()2 = − = 1 ※2乗の和は,1にはならず,すなわちcosh2xになります. (5)← (1)式の各辺を(2)式の各辺で割ると得られます. (6)← (4)の各辺をcosh2xで割ると 1−= (5)式を用いて第2項を書き換えると 1−tanh2x= (7)← (4)の各辺をsinh2xで割ると −1= (5)式を用いて第2項を書き換えると −1= |
||||||||||
|
※双曲線関数は通常,次のように読まれます. sinhx : ハイパボリックサイン coshx : ハイパボリックコサイン tanhx : ハイパボリックタンジェント ※「双曲線関数」という名称 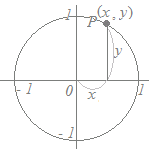
三角関数は円関数とも呼ばれ,x=cosθ , y=sinθとなる点(x , y)は円周上の点に対応しています. cos2θ+sin2θ=1  x2+y2=1 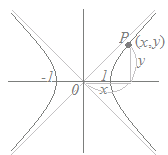
x=coshθ , y=sinhθとなる点(x , y)は双曲線上の点に対応しています. cosh2θ−sinh2θ=1  x2−y2=1 (ただし,このθは,動径OPがx軸となす角には対応しません.) ※双曲線関数に関する,その他の記号 (I) 次の関数は,各々(1)(2)(3)の逆数[分母と分子を逆にしたもの]として定義されます.
(*1) ハイパボリック・コセカントはハイパボリック・サインの逆数
cosechx= (*2) ハイパボリック・セカントはハイパボリック・コサインの逆数 sechx= (*3) ハイパボリック・コタンジェントはハイパボリック・タンジェントの逆数 cothx= ⇒いずれも赤で示した3番目の文字の逆になります. (II) 次の関数は,各々(1)(2)(3)の逆関数として定義されます.[逆関数は逆数とは全く別のものであることに注意]
(**1)
y=sinh−1x ⇔ x=sinhyとして定義され sinh−1x=log(x+)に等しい.
すなわち,x=のとき
同様にしてey−e−y=2x (ey)2−2xey−1=0 ey=x+ (>0) y=log(x+) となるから sinh−1x=log(x+) (**2) y=cosh−1x ⇔ x=coshyとして定義され cosh−1x=log(x+)に等しい. (ただし,x≧1.かつ,グラフから分かるようにy=coshxは左右対称となっているが,そのうちの第1象限の側の値とする.) (**3) y=tanh−1x ⇔ x=tanhyとして定義され tanh−1x=log( ) (−1<x<1)に等しい. |
|
III【双曲線関数の性質<取り得る値の範囲>】
(解説)y=sinhx , y=coshx , y=tanhxのグラフは次の図のようになり,−∞<x<∞のとき −∞<sinhx<∞ …(8) coshx≧1 …(9) −1<tanhx<1 …(10) になります. 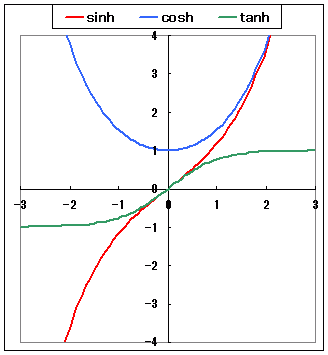 y=sinhx=のグラフのおおよその見当をつけるには, まずy=exのグラフとy=e−xのグラフを思い浮かべて,次にそれらの差をとります. ○ 原点を通ります x=0のときは,e0=1 , e−0=1となるので,e0−e−0=0です.(したがって,÷2も0となって,原点を通ります.) ○ 単調増加で,限りなく増加します xが増加すると,exは限りなく増加し,e−xは0に近づいて無視できるようになるので,全体として限りなく増加します.(したがって,÷2も限りなく増加します.) ○ 奇関数で,原点に関して対称になります 後に述べるように原点に関して対称なグラフになります. 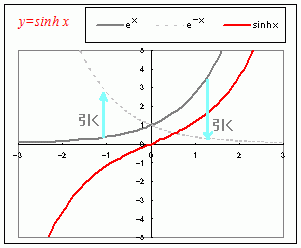 |
|
y=coshx=のグラフのおおよその見当をつけるには, まずy=exのグラフとy=e−xのグラフを思い浮かべて,次にそれらの真中を見ます. ○ 常にy=coshx≧1です. ex=X (>0)とおくと,(相加平均)≧(相乗平均)の関係のときに習ったように ≧1(等号成立はX=1のとき.すなわちx=0のとき) だから,coshxの値は,常に1以上になり,これよりも小さな値はとりません. ○ y軸に関して対称なグラフになります つまり,y=coshxの値とy=cosh(−x)の値は等しくなるので,1よりも大きなyの値に対して,それを与えるxの値は,符号が異なる2つずつあります. 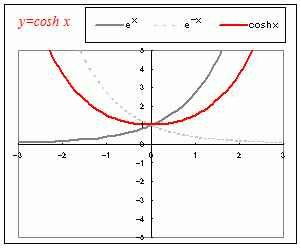 =1−2だから,つねに1よりも小さくなる ことに注意します. また,=−1+2だから,つねに−1よりも大きく なることに注意します.(1と−1の間だけをとります.) ○ 奇関数で,原点を通り,原点に関して対称になります 後に述べるように原点に関して対称なグラフになります. 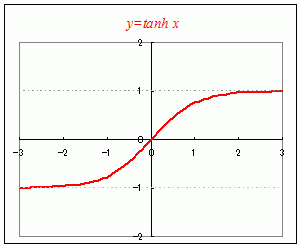 |
|
IV【双曲線関数の性質<偶関数・奇関数>】
偶関数・奇関数の性質は,三角関数の場合と同じです. |
||||||||
|
(解説) (11)← (1)によりsinh(−x)== − sinhx (12)← (2)によりcosh(−x)==coshx (13)← (3)によりtanh(−x)== − tanhx |
|
【例題1】
(解答)sinhx=のとき,coshx , tanhxの値を求めてください. (4)式に代入
cosh2x−()2=1
coshx=…(答)cosh2x= coshx=± coshx≧1>0だから tanhx==…(答) |
|
(Excelを使って解くには) Excelのワークシート関数で,sinhx, coshx, tanhxは各々SINH(), COSH(), TANH()です. また,sinh−1x, cos−1x, tanh−1xは各々ASINH(), ACOSH(), ATANH()です. そこで,例えばセルA1にsinhxの値を=4/3と書きこみます. 次に,セルA2に =ASINH(A1) とすると,xの値が計算されますので, さらに,セルA3に =ACOSH(A2) とすると,coshxの値が計算されますが,そのままでは小数なのでこれを分数になおすために,書式→セル→分数→1桁増加 とすると,1 2/3 と表示され,これが帯分数の1+2/3すなわち5/3を表すことになります. 同様にして,セルA4に =ATANH(A2) とすると,tanhxの値が計算され,上記と同様に分数表示にすると 4/5 になります. |
|
【例題2】
(解答)tanhx= − のとき,sinhx , coshxの値を求めてください. ※(注) (5)式に代入すると,sinhxとcoshxの比しかわからず,各々の値は求まらないことに注意してください.また,tanhxの分母と分子がそのままで,sinhxとcoshxに対応しているといった初歩的なミスをしてはいけません.与えられた比となる分数は幾らでもあり === ...などはすべてに等しくなります. (6)式に代入 1−( − )2= 1− = = cosh2x=4 coshx≧1>0だから coshx=2 sinhx=tanhx×cosh= −
(7)を用いて,sinhxを先に求めてもよい.その場合は,tanhx<0のときはsinhx<0を使って符号を決めます.
|
|
(Excelを使って解くには) 例えばセルA1にtanhxの値− を=-SQRT(3)/2と書きこみます. 次に,セルA2に =ATANH(A1) とすると,xの値が計算されますので, さらに,セルA3に =ACOSH(A2) とすると,coshxの値が計算されます.(整数で表示されます) 同様にして,セルA4に =ASINH(A2) とすると,sinhxの値が計算され,-1.732050808という小数になります. これは,− を表す根号なので,分数表示に直しても近似値になるだけです.「富士山麓オーム鳴く」という語呂合わせを覚えていれば,あああれのことかと見当が付きますが,そうでなければこのような場合に,どのような無理数に対応しているのかを必ず言い当てる方法はないと思います. ただし,この問題については =A4^2 により,正確に 3 という値が得られますので,セルA4が− を表すことは確かめられます. |
|
正しい番号を選択してください.
[問題1]
sinhx= のとき,coshx , tanhxの値を求めてください. 1coshx= , tanhx= 2coshx= , tanhx= 3coshx= , tanhx= 4coshx= , tanhx= HELP
(4)式に代入
cosh2x−()2=1
coshx=cosh2x= coshx=± coshx≧1>0だから tanhx== →2
|
|
[問題2]
tanhx= のとき,sinhx , coshxの値を求めてください. 1sinhx= , coshx= 2sinhx= , coshx= 3sinhx= , coshx= 4sinhx= , coshx= HELP
(6)式に代入
1−( )2= 1− = = cosh2x= coshx≧1>0だから coshx= sinhx=tanhx×coshx= →4
|
|
V【双曲線関数の性質<加法定理>】三角関数との符号の比較
tanh(α±β)の分母も逆になる〜♪ |
||||||||||||
|
(解説) (14)← sinh(α+β)= sinhα coshβ+coshα sinhβ =+ =+ == したがって,sinh(α+β)=sinhα coshβ+coshα sinhβ (15)← sinh(α+(−β))=sinhα cosh(−β)+coshα sinh(−β) 偶関数・奇関数の性質(11)(12)により cosh(−β)=coshβ, sinh(−β)=sinhβ だから,これは sinhα coshβ−coshα sinhβに等しい. (16)← cosh(α+β)= coshα coshβ+sinhα sinhβ =+ =+ == したがって,cosh(α+β)=coshα coshβ+sinhα sinhβ (17)← cosh(α+(−β))=coshα cosh(−β)+sinhα sinh(−β) 偶関数・奇関数の性質(11)(12)により cosh(−β)=coshβ, sinh(−β)=sinhβ だから,これは coshα coshβ−sinhα sinhβに等しい. (18)← tanh(α+β)== = = したがってtanh(α+β)= (19)← tanh(α+(−β))= 偶関数・奇関数の性質(13)により tanh(−β)= − tanhβ だから,これは に等しい. |