← PC用は別頁
|
○ 無理関数のグラフ
--図1--
(1) y=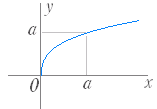
(a>0,定義域:x≧0,値域:y≧0) のグラフは図1のようになる.
【例】
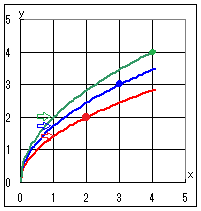
⇒で示した点は,x=1 , y=を表す.
図において青で示したものはy=のグラフで,●で示した点は,x=2 , y=2を表す.
⇒で示した点は,x=1 , y=を表す.
図において緑で示したものはy=のグラフで,●で示した点は,x=3 , y=3を表す.
⇒で示した点は,x=1 , y==2を表す.
●で示した点は,x=4 , y=4を表す.
--図2--
(2) y=−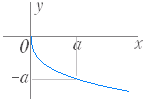
( a>0,定義域:x≧0,値域:y≦0 ) のグラフは y= のグラフを x 軸に関して対称に移動したもので図2のようになる.
【例】
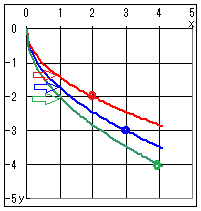
⇒で示した点は,x=1 , y=−を表す.
図において青で示したものはy=−のグラフで,●で示した点は,x=2 , y=−2を表す.
⇒で示した点は,x=1 , y=−を表す.
図において緑で示したものはy=−のグラフで,●で示した点は,x=3 , y=3を表す.
⇒で示した点は,x=1 , y=−=−2を表す.
●で示した点は,x=4 , y=−4を表す.
--図3--
(3) y=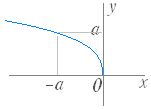
( a>0,定義域:x≦0,値域:y≧0 ) のグラフは y= のグラフを y 軸に関して対称に移動したもので図3のようになる.
【例】
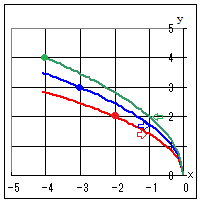
⇒で示した点は,x=−1 , y=を表す.
図において青で示したものはy=のグラフで,●で示した点は,x=−2 , y=2を表す.
⇒で示した点は,x=−1 , y=を表す.
図において緑で示したものはy=のグラフで,●で示した点は,x=−3 , y=3を表す.
⇒で示した点は,x=−1 , y==2を表す.
●で示した点は,x=−4 , y=4を表す.
--図4--
(4) y=−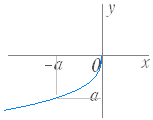
( a>0,定義域:x≦0,値域:y≦0 ) のグラフは y= のグラフを原点に関して対称に移動したもので図4のようになる.
【例】
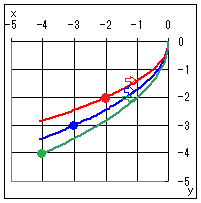
⇒で示した点は,x=−1 , y=−を表す.
図において青で示したものはy=−のグラフで,●で示した点は,x=−2 , y=−2を表す.
⇒で示した点は,x=−1 , y=−を表す.
図において緑で示したものはy=−のグラフで,●で示した点は,x=−3 , y=−3を表す.
⇒で示した点は,x=−1 , y=−=−2を表す.
●で示した点は,x=−4 , y=−4を表す. |
|
○ 無理関数のグラフの平行移動 (1) y= のグラフを x 軸の正の向きに p, y 軸の正の向きに q だけ平行移動してできるグラフの方程式は, y= +q になる. 元のグラフが,y=− , y= , y=− のときも同様 |
|
例 y= +3 のグラフ 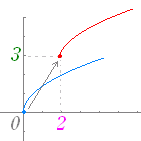 y=−2 のグラフ 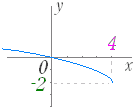 y= のグラフを描くときは,y= に変形して考えるとよい. 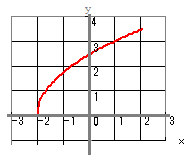 y=2 のグラフを描くときは,y= に変形して考えるとよい. 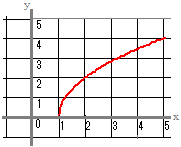 |
|
問題1 次の関数のグラフを右下から選べ. ○初めに左から関数を選び,続いてグラフを選べ.グラフの側にはジョーカーが含まれている. ○正しければ消える.間違っていれば消えない. 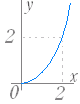 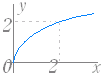 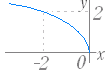 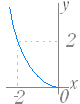 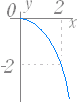
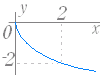
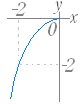
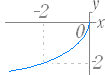 |
|
問題2 次の関数のグラフを選べ. ○初めに左から関数を選び,続いてグラフを選べ.グラフの側にはジョーカーが含まれている. ○正しければ消える.間違っていれば消えない. 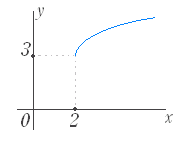 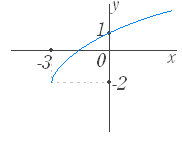 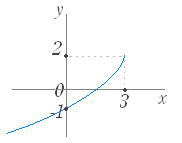 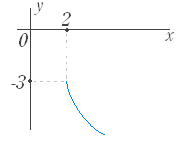 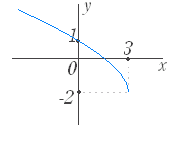 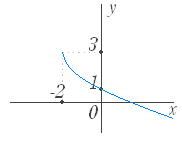
|
|
[注]直前にPC版から入られた場合は,自動転送でスマホ版に来ていますので,ブラウザの[戻るキー]では戻れません(堂々巡りになる).下記のリンクを使ってメニューに戻ってください.
|