== 累乗根と分数指数（有理指数） ==
※この頁は，「無理関数の微分」の予備段階として累乗根を分数指数（有理指数）に読み替える練習を行うものです．この頁ではまだ微分は扱っていません．
■ 次の左欄に対応するものを，右欄から選びなさい。
○初めに累乗根の形から１つ選んで●をクリックし，続いて右の有理指数の形から●を１つクリックしなさい。
○結果は，下端の記号のようになり，全部 ● になれば完了です。
記号 → ●：未処理，●：処理中，●：正解
○間違ったときは，個別の問題についてHELPを読むことができますが，HELPを読む場合も読まない場合も新たに問題を選択すれば，解答を再開できます．
･･･  [全体のHelpを読む]
○ 累乗根の形の無理関数を分数指数を用いて表わすには，次の公式を用います。
また，分母にあるときは負の指数に変えればよいから，
○ 特別なものとして，
があります。
→ 閉じる  ←
●^4} ) \( \displaystyle \sqrt[3]{(x-1)^4} \)
●
^3}}) \( \displaystyle \frac{1}{\sqrt[4]{(x-1)^3}} \)
●
^5}}{\sqrt[4]{(x-1)^3}}) \( \displaystyle \frac{\sqrt[2]{(x+ 1)^5}}{\sqrt[4]{(x-1)^3}} \)
●
 \( \displaystyle \sqrt[3]{x+ 1}\sqrt{x-1} \)
●
^3}}) \( \displaystyle \sqrt[4]{(x-1)^3} \)
●
 \( \displaystyle \frac{1}{\sqrt{x-1}} \)
●
^2}}{\sqrt[3]{(x-1)^4}}) \( \displaystyle \frac{\sqrt[5]{(x+ 1)^2}}{\sqrt[3]{(x-1)^4}} \)
●
 \( \displaystyle \frac{\sqrt{x-1}}{\sqrt[3]{x+1}} \)
●
^{\frac{1}{2}}(x%2B 1)^{-\frac{1}{3}}) \( \displaystyle (x-1)^{\frac{1}{2}}(x+ 1)^{-\frac{1}{3}} \)
●
^{\frac{2}{5}}(x-1)^{-\frac{4}{3}}) \( \displaystyle (x+1)^{\frac{2}{5}}(x-1)^{-\frac{4}{3}} \)
●
^{\frac{1}{3}}(x-1)^{\frac{1}{2}}) \( \displaystyle (x+ 1)^{\frac{1}{3}}(x-1)^{\frac{1}{2}} \)
●
^{\frac{3}{4}}) \( \displaystyle (x-1)^{\frac{3}{4}} \)
●
^{-\frac{1}{2}}) \( \displaystyle (x-1)^{-\frac{1}{2}} \)
●
^{\frac{5}{2}}(x-1)^{-\frac{3}{4}}) \( \displaystyle (x+1)^{\frac{5}{2}}(x-1)^{-\frac{3}{4}} \)
●
^{\frac{4}{3}}) \( \displaystyle (x-1)^{\frac{4}{3}} \)
●
^{-\frac{3}{4}}) \( \displaystyle (x-1)^{-\frac{3}{4}} \)
HELP
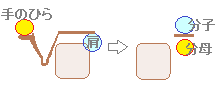
「手のひら」は分母に，「肩」は分子に，分数の指数を作る
［公式］ \( \displaystyle \sqrt[n]{a^m}=a^{\frac{m}{n}} \)
に当てはめると，^4}=(x-1)^{\frac{4}{3}}&chco=aa4422) \( \displaystyle \sqrt[3]{(x-1)^4}=(x-1)^{\frac{4}{3}} \)
分母は^3}=(x-1)^{\frac{3}{4}}&chco=aa4422) \( \displaystyle \sqrt[4]{(x-1)^3}=(x-1)^{\frac{3}{4}} \)
全体は^3}}=(x-1)^{-\frac{3}{4}}&chco=aa4422) \( \displaystyle \frac{1}{\sqrt[4]{(x-1)^3}}=(x-1)^{-\frac{3}{4}} \)
分子は^5}=(x%2B 1)^{\frac{5}{2}}&chco=aa4422) \( \displaystyle \sqrt[2]{(x+1)^5}=(x+ 1)^{\frac{5}{2}} \)
分母は\( \displaystyle \sqrt[4]{(x-1)^3}=(x-1)^{\frac{3}{4}} \)
全体は^{\frac{5}{2}}}{(x-1)^{\frac{3}{4}}}=(x%2B 1)^{\frac{5}{2}}}(x-1)^{-\frac{3}{4}}&chco=aa4422) \( \displaystyle \frac{(x+ 1)^{\frac{5}{2}}}{(x-1)^{\frac{3}{4}}}=(x+ 1)^{\frac{5}{2}}(x-1)^{-\frac{3}{4}} \)
^{\frac{1}{3}}&chco=aa4422) \( \displaystyle \sqrt[3]{x+ 1}=(x+ 1)^{\frac{1}{3}} \)
^{\frac{1}{2}}&chco=aa4422) \( \displaystyle \sqrt{x-1}=(x-1)^{\frac{1}{2}} \)
だから^{\frac{1}{3}}(x-1)^{\frac{1}{2}}&chco=aa4422) \( \displaystyle (x+1)^{\frac{1}{3}}(x-1)^{\frac{1}{2}} \)
「手のひら」は分母に，「肩」は分子に，分数の指数を作る
［公式］\( \displaystyle \sqrt[n]{a^m}=a^{\frac{m}{n}} \)
に当てはめると
\( \displaystyle \sqrt[4]{(x-1)^3}=(x-1)^{\frac{3}{4}} \)
分母は\( \displaystyle \sqrt{x-1}=(x-1)^{\frac{1}{2}} \)
全体は^{\frac{1}{2}}}=(x-1)^{-\frac{1}{2}}&chco=aa4422) \( \displaystyle \frac{1}{(x-1)^{\frac{1}{2}}}=(x-1)^{-\frac{1}{2}} \)
分子は^2}=(x%2B 1)^{\frac{2}{5}}&chco=aa4422) \( \displaystyle \sqrt[5]{(x+ 1)^2}=(x+ 1)^{\frac{2}{5}} \)
分母は\( \displaystyle \sqrt[3]{(x-1)^4}=(x-1)^{\frac{4}{3}} \)
全体は^{\frac{2}{5}}}{(x-1)^{\frac{4}{3}}}=(x%2B 1)^{\frac{2}{5}}}(x-1)^{-\frac{4}{3}}&chco=aa4422) \( \displaystyle \frac{(x+ 1)^{\frac{2}{5}}}{(x-1)^{\frac{4}{3}}}=(x+ 1)^{\frac{2}{5}}(x-1)^{-\frac{4}{3}} \)
分子は\( \displaystyle \sqrt{x-1}=(x-1)^{\frac{1}{2}} \)
分母は^{\frac{1}{3}}&chco=aa4422) \( \displaystyle \sqrt[3]{x+ 1}=(x+ 1)^{\frac{1}{3}} \)
全体は^{\frac{1}{2}}}{(x%2B 1)^{\frac{1}{3}}}=(x-1)^{\frac{1}{2}}(x%2B 1)^{-\frac{1}{3}}&chco=aa4422) \( \displaystyle \frac{(x-1)^{\frac{1}{2}}}{(x+ 1)^{\frac{1}{3}}}=(x-1)^{\frac{1}{2}}(x+ 1)^{-\frac{1}{3}} \)
|
...（携帯版）メニューに戻る
合成関数