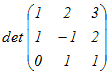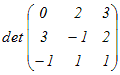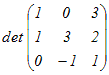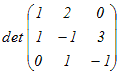■ Excelによる解き方
○ 上のような方法で連立方程式の解が求められるということが分かれば，実際の数値計算はExcelによって行うことができる．･･･ただし，Excelでは解は小数（または指数表示）で示されるので，
▼「解が分数になるときに，どのような分数を表しているかを調べるには工夫を要する」 …(***)
▼「解が  √5nnnnのような無理数になるときに近似値で表された小数から元の無理数を推測するのは難しい」
(***) 右のA5:C7のように数値が分数になるときは，分母が3桁以下なら「セルの書式→分数→3桁増加」により，分数表示される．このとき，仮分数は対分数を使って表示される（ 4/3 → 1 1/3 など）．また，負の仮分数は整数部分にのみ符号が付く（ -4/3 → -1 1/3 など）
元の係数行列や定数項が整数で,求めた逆行列や解の分母が４桁以上の分数になるときは，分母がdet(A)になることが原因なので，det(A)倍しておくと整数係数になる･･･ただし，結果もdet(A)倍になっていることを途中で忘れてはいけない．
| |
A |
B |
C |
D |
E |
F |
G |
| 1 |
1 |
2 |
3 |
|
2 |
|
0.000 |
| 2 |
1 |
-1 |
2 |
|
-1 |
|
3.000 |
| 3 |
0 |
1 |
1 |
|
0 |
|
-1.000 |
| 4 |
|
|
|
|
|
|
|
| 5 |
1 1/2 |
- 1/2 |
-3 1/2 |
|
0 |
|
2.000 |
| 6 |
1/2 |
- 1/2 |
- 1/2 |
|
3 |
|
-1.000 |
| 7 |
- 1/2 |
1/2 |
1 1/2 |
|
-1 |
|
0.000 |
○ ［逆行列による方法］で連立方程式をExcelで解くには次のようにすればよい．
(1) 行列の成分は，右図のように各セルに数値を入力する．
(2) 逆行列を求めるワークシート関数としてMINVERSE()を利用する．
(3) 行列の積を求めるワークシート関数としてMMULT()を利用し，これによって解を求めるとともに検算する．
(1) 黄色で示したように係数行列を入力する：これが行列A
もも色で示したE1:E3の部分は，はじめは空欄にしておく．G1:G3も空白にしておく･･･これらは検算用に使う．
(2) 灰色で示した部分に行列Aの逆行列を求める．
セルA5に =MINVERSE(A1:C3) と書き込む．
（直接入力してもよい．関数の挿入からメニューをたどって書き込んでいくときは，
・fxをクリックして関数の挿入メニューを出す
・関数の分類は「すべて表示」または「数学/三角」とする
・関数名はMINVERSEとする → OK
・配列で元の行列Aの範囲を選択する）
※このとき逆行列の各成分が自動的に書き込まれるのでなくA5には逆行列の(1,1)成分（=単なる数値１つのもの）が書き込まれるので，これをA5:C7の範囲に配列として書き込むためには
A5:C7の範囲を選択し反転表示にする
画面上にある数式バーのどこかをポイントしてから
Ctrl+Shiftを押しながらEnterキーを押す
(3) 次に行列の積A−1 −−>bwを計算するためにE5:E7（水色の部分）に問題の右辺にあった定数項の列ベクトルを書き込む．
・「行ベクトルと行ベクトルの積」（横向きの並びと横向きの並びの積）や「列ベクトルと列ベクトルの積（縦向きの並びと縦向きの並びの積）」を求めるには=SUMPRODUCT(範囲１：範囲２)とするが，今行いたいのは「行×列＝行列の各成分」という計算で，これを求める関数はMMULT(行列１：行列２)となっている．
・G5に=MMULT(A5:C7,E5:E7)と書きこむ． （直接入力してもよい．関数の挿入からメニューをたどって書き込んでいくときは，
・fxをクリックして関数の挿入メニューを出す
・関数の分類は「すべて表示」または「数学/三角」とする
・関数名はMMULTとする → OK
・配列で行列 A−1の範囲を選択してから「カンマ」を入れて，次にベクトル −−>bwの範囲を選択する）
※左に青で示したときと同様に，配列（行列）にするにはG5:G7の範囲を選択してから Ctrl+Shift+Enter とする．
Excelでは数値の表示設定次第では小数が四捨五入されて整数でない数値も整数で表示されることがあるので，小数の桁も表示されるようにしておくと早合点しなくて済む．
実際に計算すると「範囲選択のミス」「関数のとり違い」「考え方の間違い」など様々な間違いが起こるので，検算しておくとよい．そのためには，元の行列行列 Aと求めた解との積が右辺の定数ベクトルになっていることを確かめればよいので，E1:E3に解のベクトルを書き込み，G1：G3にそれらの積を求めてベクトル −−>bwと一致していることを確かめるとよい．
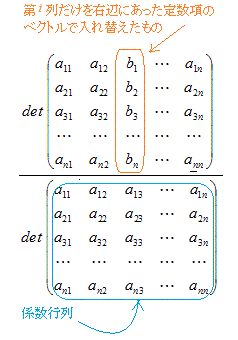
○ ［クラメールの公式］で連立方程式をExcelで解くには次のようにすればよい．
・係数行列と右辺の定数項からなる列ベクトルを用意する．
・係数行列をコピーしたものを必要個数作り，各々の１列目，２列目，･･･にベクトル −−>bwを上書きする．
・行列式を求める関数 MDETERM(行列の範囲) を使って，各々の行列式を求める･･･これらは単なる数字になる．
・求めたdet(A)で順に割れば答になる．
|
...�域声蟶ｯ迚茨ｼ峨Γ繝九Η繝ｼ縺ｫ謌ｻ繧�
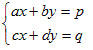…(*1)は，行列を用いて
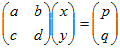…(*2)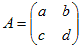
を係数行列という．
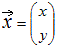で表され，右辺の定数項の組は列ベクトル（２×１行列）
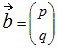で表される．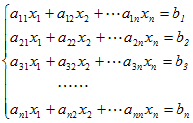
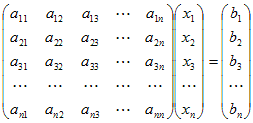
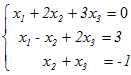
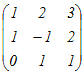の逆行列を求めると
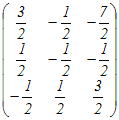となるから，
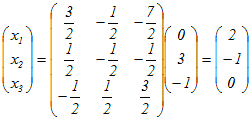…（答）
