← PC用は別頁
|
※ 前提となる事柄
[基本]
・無理関数の導関数は,高校の数学IIIに登場します。 ・「微分する」と「導関数を求める」とは同じ意味です。 ・無理関数の導関数は,無理関数及び導関数が定義されるところでのみ考えます。通常√の中が0以上であること,(分母があるときは)分母が0でないことなどが前提ですが,特に断らずそれらの条件を満たしているところでのみ考えます。
|
|
例題1
[答案例]  |
|
※以下の問題で,
「正答の場合に表示される図」⇒  「誤答の場合に表示される図」⇒  ---------------- ※解答すれば,解説が読めます.解答しなければ,解説は出ません.
[問題1]・・・・・(計算用紙が必要です。)・・・・・
|
|
|
|
 |
|
解説 |
|
[累乗根形式]
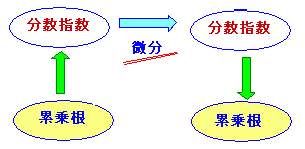 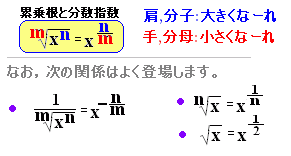
例題2
y= [答案例] 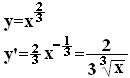 ・・・答 ・・・答 |
|
[問題2]・・・・・(計算用紙が必要です。)・・・・・
|
|
|
|
 |
|
解説 |
|
|
[合成関数1]
例題3
[答案例1] 合成関数は,「階段を作る」
 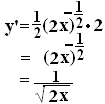 ・・・答 ・・・答 |
|
[問題3]・・・・・(計算用紙が必要です。)・・・・・
|
|
|
|
 |
|
解説 |
|
|
[合成関数2]
例題4
[答案例] 「階段を作る」でやれば・・
例題5
[答案例] 「玉ねぎ,皮むき」でやれば・・・ 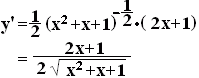 ・・・答 ・・・答 |
|
[問題4]・・・・・(計算用紙が必要です。)・・・・・
|
|
|
|
 |
|
解説 |
|
|
[問題5]・・・・・(計算用紙が必要です。)・・・・・
|
|
|
|
 |
|
解説 |
|
|
[積の微分との組合せ]
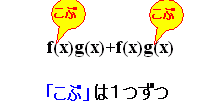
例題6
[答案例] 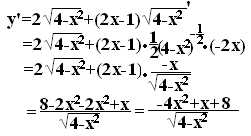 ・・・答 ・・・答
[商の微分との組合せ]
商の微分( f は負けて勝つ) 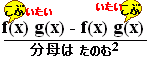
例題7
[答案例]
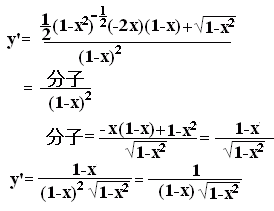 ・・・答 ・・・答 |
|
※ 積や商の数が多いとき(例えば3個以上)は,対数微分法によります。(後出)
|
|
[問題6]・・・・・(計算用紙が必要です。)・・・・・
|
|
|
|
 |
|
解説 |
|
|
[問題7]・・・・・(計算用紙が必要です。)・・・・・
|
|
|
|
 |
|
解説 |
|
|
|