|
*** ђ”Љw‡UЃi‘ЅЌЂЋ®‚Ь‚ЕЃj ***
 •s’иЊ`‚М‹ЙЊА •s’иЊ`‚М‹ЙЊА
 ”ч•ЄЊWђ” ”ч•ЄЊWђ”
 “±ЉЦђ”‚М’и‹` “±ЉЦђ”‚М’и‹` ђЪђь‚М•ы’цЋ® ђЪђь‚М•ы’цЋ®
 ‘ќЊё•\ ‘ќЊё•\
 “±ЉЦђ”‚М•„Ќ†‚М‹Ѓ‚Я•ы “±ЉЦђ”‚М•„Ќ†‚М‹Ѓ‚Я•ы
|
|
*** ђ”Љw‡UЃi‘ЅЌЂЋ®‚Ь‚ЕЃj ***
 •s’иЊ`‚М‹ЙЊА •s’иЊ`‚М‹ЙЊА
 ”ч•ЄЊWђ” ”ч•ЄЊWђ”
 “±ЉЦђ”‚М’и‹` “±ЉЦђ”‚М’и‹` ђЪђь‚М•ы’цЋ® ђЪђь‚М•ы’цЋ®
 ‘ќЊё•\ ‘ќЊё•\
 “±ЉЦђ”‚М•„Ќ†‚М‹Ѓ‚Я•ы “±ЉЦђ”‚М•„Ќ†‚М‹Ѓ‚Я•ы
|
|
Ѓy—v“_Ѓz
(1)Ѓ@x, yЌА•W‚Є‚»‚к‚ј‚к‘ж‚R‚М•Пђ”t‚р—p‚ў‚Д
(2)Ѓ@x, y‚Є”}‰о•Пђ”‚Е•\‚і‚к‚йЉЦђ”t‚р—p‚ў‚Д•\‚і‚к‚й‚Ж‚«ЃC‚»‚М“±ЉЦђ”Ѓi”ч•ЄЃj‚Н
==
(3)Ѓ@€к”К‚ЙЃC“_P(a, b)‚р’К‚иЃCЊX‚«m‚М’јђь‚М•ы’цЋ®‚Н
y−b=m(x−a)‚Ж‚И‚й‚М‚ЕЃCЏг‹L‚М”}‰о•Пђ”•\Ћ¦(*)‚Й‚В‚ў‚Дt=t0‚М‚Ж‚«‚М ЃmђЪђь‚М•ы’цЋ®Ѓn‚Н
y−g(t0)=(x−f(t0))
Ѓm–@ђь‚М•ы’цЋ®Ѓn‚Н
y−g(t0)=−(x−f(t0))
(4)Ѓ@“®“_P(x, y)‚МЌА•W‚ЄЃCЏг‹L‚М”}‰о•Пђ”•\Ћ¦(*)‚Е—^‚¦‚з‚к‚й‚Ж‚«ЃC‚»‚М‘¬“x‚Мxђ¬•Єvx‚Ё‚ж‚Сyђ¬•Єvy‚Н
=(f’(t) , g’(t) )
‚Е‹Ѓ‚Я‚з‚к‚йЃDЃ@‚Ь‚ЅЃC‰Б‘¬“x‚Мxђ¬•Єax‚Ё‚ж‚Сyђ¬•Єay‚Н
=(f”(t) , g”(t) )
‚Е‹Ѓ‚Я‚з‚к‚йЃDЃy‰рђаЃz (2) ← Ѓ@y‚рx‚Е”ч•Є‚µ‚Ѕ“±ЉЦђ”Ѓi”ч•ЄЃj‚НЃC’P‚И‚й•Єђ”‚Е‚Н‚И‚ў ‚М‚Еd‚ѕ‚Ї–с•Є‚·‚й‚悤‚И‚±‚Ж‚Н‚Е‚«‚Ь‚№‚сЃD Ѓ@‚µ‚©‚µЃC“±ЉЦђ”Ѓi”ч•ЄЃj‚НЃC•Ѕ‹П•П‰»—¦‚М‹ЙЊА‚Ж‚µ‚Д ’и‹`‚і‚к‚Д‚Ё‚иЃC = •Ѕ‹П•П‰»—¦‚М’iЉK‚Е‚НЃC•Ѓ’К‚М•Єђ”‚ЕЃCЉ|‚ЇЋZЃEЉ„‚иЋZ‚в –с•Є‚И‚З‚Є‚Е‚«‚Ь‚·ЃD‚»‚±‚ЕЃC•Є•к‚Ж•ЄЋq‚рΔt‚ЕЉ„‚й‚Ж = ‚±‚МЋ®‚Й‚Ё‚ў‚ДЃCΔx→0Ѓi‚±‚М‚Ж‚«ЃC“ЇЋћ‚ЙΔt→0‚Ж‚И‚йЃj‚М‹ЙЊА‚рЌl‚¦‚й‚Ж = ‚Ж‚И‚и‚Ь‚·ЃD‚±‚М—ј•У‚р”ч•Є‹LЌ†‚Е•\‚·‚Ж = |
|||||||
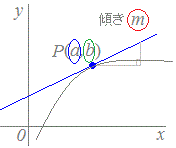 (3) ←
(3) ←Ѓ@‹ИђьЏг‚М“_P(a, b)‚Й‚Ё‚Ї‚й”ч•ЄЊWђ”‚НЃC“±ЉЦђ” Ѓi‚Й ‚»‚Мx‚М’l‚р‘г“ь‚µ‚Ѕ‚а‚МЃj‚Е‹Ѓ‚Я‚з‚к‚й‚©‚зЃC“_P(a, b)‚Й‚Ё‚Ї‚йђЪђь‚М•ы’цЋ®‚Й‚Ё‚ў‚Д ЊX‚«‚Нm= ‚Ь‚Ѕ xЌА•W‚Нa=f(t0) yЌА•W‚Нb=g(t0) ‚ѕ‚©‚зЃCђЪђь‚М•ы’цЋ®‚Нy−b=m(x−a)‚Й‚±‚М’l‚р‘г“ь‚µ‚Д y−g(t0)=(x−f(t0)) ‚Е‹Ѓ‚Я‚з‚к‚Ь‚·ЃD 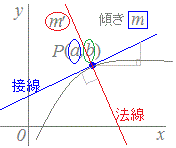 Ѓ@–@ђь‚НЃCђЪђь‚Йђ‚’јЃi’јЉpЃj‚И’јђь‚ЕЃC€к”К‚ЙЊX‚«m‚М’јђь‚Йђ‚’јЃi’јЉpЃj‚И’јђь‚МЊX‚«m’‚Н
m’=−
Ѓ@–@ђь‚НЃCђЪђь‚Йђ‚’јЃi’јЉpЃj‚И’јђь‚ЕЃC€к”К‚ЙЊX‚«m‚М’јђь‚Йђ‚’јЃi’јЉpЃj‚И’јђь‚МЊX‚«m’‚Н
m’=−‚Й‚И‚и‚Ь‚·ЃD‚µ‚Ѕ‚Є‚Б‚ДЃCђЪђь ‚МЊX‚«m=‚Йђ‚’ј‚И –@ђь‚МЊX‚«‚Нm’=−‚Й‚И‚й‚М‚ЕЃC “_P(a, b)‚р’К‚иЃCЊX‚«m’=−‚М’јђь‚М•ы’цЋ®‚Н y−g(t0)=−(x−f(t0)) |
|
–в‚P”}‰о•Пђ”‚Е•\‚і‚к‚ЅЋџ‚МЉЦђ”‚Й‚В‚ў‚ДЃC“±ЉЦђ”‚рt‚МЉЦђ”‚Ж‚µ‚Д•\‚µ‚Д‚‚ѕ‚і‚ўЃD
1
2
3
4
HELP
=2t+2, =2t
‚ѕ‚©‚з === → 3
|
||
|
–в‚Q”}‰о•Пђ”‚Е•\‚і‚к‚ЅЋџ‚МЉЦђ”‚Й‚В‚ў‚ДЃC“±ЉЦђ”‚рt‚МЉЦђ”‚Ж‚µ‚Д•\‚µ‚Д‚‚ѕ‚і‚ўЃD
1tant
2−tant
3
4−
HELP
=acost, =−bsint
‚ѕ‚©‚з ==−=−tant → 2
|
|
–в‚RЋџ‚М”}‰о•Пђ”‚Е•\‚і‚к‚Ѕ‹Иђь‚Й‚В‚ў‚ДЃCЃiЃ@Ѓ@Ѓj“а‚Мt‚М’l‚Й‘О‰ћ‚·‚й“_‚Й‚Ё‚Ї‚йђЪђь‚М•ы’цЋ®‚р‹Ѓ‚Я‚Д‚‚ѕ‚і‚ўЃD
1y=x+
2y=x−
3y=−x+
4y=−x−
HELP
=1+cost, =sint
‚ѕ‚©‚з == t=‚М‚Ж‚« x=+1 y=1 =1 ‚ѕ‚©‚з y−1=x−( +1) y=x− → 2
Ѓ¦ЃiЋQЌlЃjЃ@Ћџ‚Мђ}‚̂悤‚ЙЃC‚±‚МѓOѓ‰ѓt‚Н•WЏЂ“I‚ИѓTѓCѓNѓЌѓCѓh‹ИђьЃFЃmђФ‚ЕЋ¦‚µ‚Ѕ‚а‚МЃn
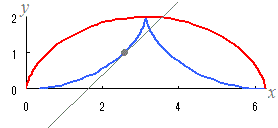 |
|||||
|
–в‚SЋџ‚М”}‰о•Пђ”‚Е•\‚і‚к‚Ѕ‹Иђь‚Й‚В‚ў‚ДЃCЃiЃ@Ѓ@Ѓj“а‚Мt‚М’l‚Й‘О‰ћ‚·‚й“_‚Й‚Ё‚Ї‚йђЪђь‚М•ы’цЋ®‚р‹Ѓ‚Я‚Д‚‚ѕ‚і‚ўЃD
1y=2x+2
2y=2x+3
3y=3x+2
4y=3x+3
HELP
=2t−1, =2t+1
‚ѕ‚©‚з == t=1‚М‚Ж‚« x=0 y=2 =3 ‚Ж‚И‚Б‚ДЃCђЪђь‚М•ы’цЋ®‚Н y−2=3x y=3x+2 Ѓ¦ЃiЋQЌlЃj Ѓ@Ћџ‚Мђ}‚̂悤‚ЙЃC‚±‚МѓOѓ‰ѓt‚Н•ъ•Ёђь‚рЊX‚Ї‚Ѕ‚а‚М‚Ж‚И‚Б‚Д‚ў‚Ь‚·ЃD 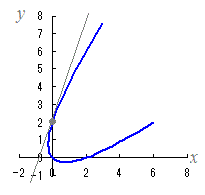 → 3
|
|
–в‚TЋџ‚М”}‰о•Пђ”‚Е•\‚і‚к‚Ѕ‹Иђь‚Й‚В‚ў‚ДЃCЃiЃ@Ѓ@Ѓj“а‚Мt‚М’l‚Й‘О‰ћ‚·‚й“_‚Й‚Ё‚Ї‚й–@ђь‚М•ы’цЋ®‚р‹Ѓ‚Я‚Д‚‚ѕ‚і‚ўЃD
1y=ex−e2
2y=−ex+e2
3y=−1 4y=−+1 HELP
=et, =
‚ѕ‚©‚з m==== m’=−tet t=1‚М‚Ж‚« x=e, y=0, m’=−e ‚Ж‚И‚Б‚ДЃC–@ђь‚М•ы’цЋ®‚Н y=−e(x−e) y=−ex+e2 Ѓ¦ЃiЋQЌlЃj Ѓ@Ћџ‚Мђ}‚Мђ…ђF‚ЄђЪђьЃCђФ‚Є–@ђь‚Й‚И‚и‚Ь‚·ЃD 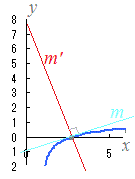 → 2
|
|||
|
–в‚UЋџ‚М”}‰о•Пђ”‚Е•\‚і‚к‚Ѕ‹Иђь‚Й‚В‚ў‚ДЃCЃiЃ@Ѓ@Ѓj“а‚Мt‚М’l‚Й‘О‰ћ‚·‚й“_‚Й‚Ё‚Ї‚й–@ђь‚М•ы’цЋ®‚р‹Ѓ‚Я‚Д‚‚ѕ‚і‚ўЃD
1y=−x+
2y=−x+1
3y=x−1 4y=x+ HELP
=− , =2
‚ѕ‚©‚з m=== m’=− t=2‚М‚Ж‚« x=, y=, m’=− ‚Ж‚И‚Б‚ДЃC–@ђь‚М•ы’цЋ®‚Н y−=−(x−) y=−x+ → 1
Ѓ¦ЃiЋQЌlЃjЃ@”}‰о•Пђ”‚рЏБ‹Ћ‚µ‚ДЊі‚МѓOѓ‰ѓt‚рx, y‚МЉЦЊWЋ®‚Е•\‚·‚ЖЃC x2+y2==2x ‚·‚И‚н‚їЃC (x−1)2+y2=1 ‚±‚к‚НЃC“_(1, 0)‚р’†ђS‚Ж‚·‚й”јЊa1‚М‰~‚Й‚И‚иЃC–@ђь‚Н’†ђS‚р’К‚и‚Ь‚·ЃDЋџ‚Мђ}‚МђВђF‚ЄђЪђьЃCђФ‚Є–@ђь‚Й‚И‚и‚Ь‚·ЃD 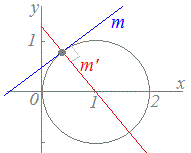 |
|
–в‚V“®“_‚М‰^“®‚ЄЋћЌЏt‚МЉЦђ”‚Ж‚µ‚ДЋџ‚М”}‰о•Пђ”‚Е•\‚і‚к‚Д‚ў‚й‚Ж‚«ЃCЃiЃ@Ѓ@Ѓj“а‚МЋћЌЏ‚Й‚Ё‚Ї‚鑬“xѓxѓNѓgѓ‹‚р‹Ѓ‚Я‚Д‚‚ѕ‚і‚ўЃD
1=(0, 1)
2=(0, −1)
3=(1, 0) 4=(−1, 0) HELP
=log t+1, =
‚ѕ‚©‚з =(log t+1, ) t=1‚М‚Ж‚« =(1, 0) → 3
Ѓ¦ЃiЋQЌlЃjЃ@Ћџ‚Мђ}‚МђВђF‚Є‹OђХЃC–о€у‚Є‘¬“x‚Й‚И‚и‚Ь‚·ЃD 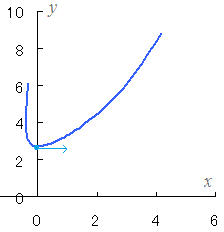 |
|||
|
–в‚W“®“_‚М‰^“®‚ЄЋћЌЏt‚МЉЦђ”‚Ж‚µ‚ДЋџ‚М”}‰о•Пђ”‚Е•\‚і‚к‚Д‚ў‚й‚Ж‚«ЃCЃiЃ@Ѓ@Ѓj“а‚МЋћЌЏ‚Й‚Ё‚Ї‚鑬“xѓxѓNѓgѓ‹‚р‹Ѓ‚Я‚Д‚‚ѕ‚і‚ўЃD
1=( , )
2=( , )
3=( , ) 4=( , ) HELP
=, =
‚ѕ‚©‚з =( , ) t=1‚М‚Ж‚« =( , )=( , ) → 4
ЃiЋQЌlЃjЃ@Ћџ‚Мђ}‚МђВђF‚Є‹OђХЃC–о€у‚Є‘¬“x‚Й‚И‚и‚Ь‚·ЃD 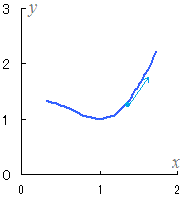 |
|
Ѓm’ЌЃn’ј‘O‚ЙPC”Е‚©‚з“ь‚з‚к‚ЅЏкЌ‡‚НЃCЋ©“®“]‘—‚ЕѓXѓ}ѓz”Е‚Й—€‚Д‚ў‚Ь‚·‚М‚ЕЃCѓuѓ‰ѓEѓU‚МЃm–Я‚йѓLЃ[Ѓn‚Е‚Н–Я‚к‚Ь‚№‚сЃi“°ЃXЏ„‚и‚Й‚И‚йЃjЃD‰є‹L‚МѓЉѓ“ѓN‚рЋg‚Б‚ДѓЃѓjѓ…Ѓ[‚Й–Я‚Б‚Д‚‚ѕ‚і‚ўЃD
|