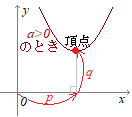
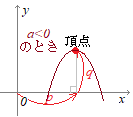
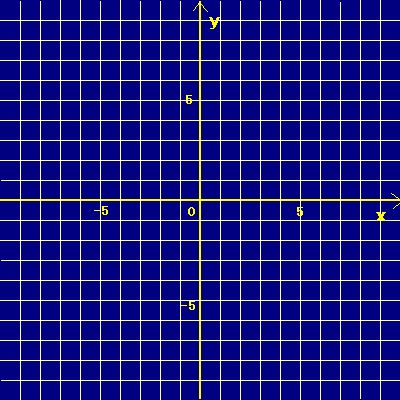
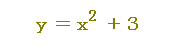← PC用は別頁
|
*** 科目 *** 数Ⅰ・A数Ⅱ・B数Ⅲ高卒・大学初年度 *** 単元 *** 数と式不等式二次関数二次不等式三角比三角比と図形集合・命題・証明順列・組合せ確率整数の性質 ※高校数学Ⅰの「2次関数」について,このサイトには次の教材があります. この頁へGoogleやYAHOO ! などの検索から直接来てしまったので前後関係がよく分からないという場合は,他の頁を先に見てください. が現在地です. ↓2次関数のグラフ(入門) ↓2次関数のグラフ[標準形] ↓平方完成の変形 ↓平方完成(演習) ↓同2 ↓展開形→頂点の座標 ↓同2 ↓同3 ↓同4 ↓同5 ↓2次関数→頂点の座標 ↓頂点の座標(文字係数1) ↓頂点の座標(文字係数2) ↓放物線の頂点を図で示す1 ↓放物線の頂点を図で示す2 ↓放物線の頂点を図で示す3(展開形) ↓2次関数のグラフの平行移動 ↓放物線の移動 ↓同2 ↓2次関数のグラフと係数の符号 ↓センター試験問題 2次関数 ↓2次関数の最大・最小(1) ↓同(2) ↓同(3) ↓同(4) ↓(t≦x≦t+1)のときの2次関数の最大値・最小値 ↓条件付2次関数の最大値・最小値 ↓2次関数のグラフと直線(文字係数) ↓解と定数の大小問題 ↓絶対値付き関数のグラフ |