|
■（例題対比）[文字係数]放物線の頂点
［基本］
○ y=a(x−p)2+qのグラフはy=ax2のグラフをx軸の正の向きにp，y軸の正の向きにqだけ平行移動したもので，その軸の方程式はx=p，頂点の座標は(p , q)である．図1→  ※ [式1]（≠0）は放物線の「形」にのみ関係しており，頂点の座標には関係ない． 例1 aを定数とするとき，２次関数（放物線) y=2(x−a)2+2a+1 の軸の方程式は x=a，頂点の座標は(a , 2a+1)になる． 例2 aを定数とするとき，２次関数（放物線) y=3(x+2a−1)2+a2+3a+4 の軸の方程式は x=−2a+1，頂点の座標は(−2a+1 , a2+3a+4)になる． ［例題1］ 次の２次関数の軸の方程式と頂点の座標を求めよ． (1) y=2(x−3a)2−4a+2 （答案) 軸x=3a，頂点(3a ,−4a+2)…（答) (2) y=−3(x−4a−1)2+a2−2a+3 （答案) 軸x=4a+1，頂点(4a+1 , a2−2a+3)…（答） |
|
図1
［問題1］ 次の２次関数の軸の方程式と頂点の座標を求めよ． (1) y=3(x−5a)2+2a−1 (2) y=−2(x−3a+5)2−3a2+2a−4 |
|
［展開形］
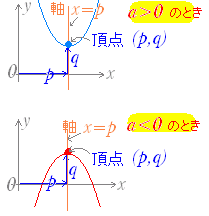
○ ２次関数が展開形で書かれているときは，これを平方完成して標準形に直せば軸の方程式，頂点の座標が分かる． ○ 次の［例題2］の変形は，抵抗なくできる生徒が多いが，［例題3,4］の変形はできない生徒が多い． ［例題2］ y=2x2−4ax+3a2−2a+3 ■x2の係数でくくる =2(x2−2ax)+3a2−2a+3 ■( .. )の中を平方完成する．xの係数の半分を持ってくる． =2{ (x−a)2−a2}+3a2−2a+3 ■外側の{ .. }をはずす =2(x−a)2−2a2+3a2−2a+3 ■定数項を簡単にして仕上げる =2(x−a)2+(a2−2a+3) 頂点の座標は(a , a2−2a+3) ［例題3］ y=2x2+4ax+a2−8x−5a+4 ■xについて整理する …★ =2x2+(4a−8)x+(a2−5a+4) ■x2の係数でくくる（定数項は後回し) =2{ x2+(2a−4)x }+(a2−5a+4) ■{ .. }の中を平方完成する．xの係数の半分を持ってくる． =2{ (x+a−2)2−(a−2)2}+(a2−5a+4) ■外側の{ .. }をはずす =2(x+a−2)2−2a2+8a−8+a2−5a+4 ■定数項を簡単にして仕上げる =2(x+a−2)2−a2+3a−4 頂点の座標は(−a+2 ,−a2+3a−4) ※ ［例題3］の変形で鍵となるのは，★で示した箇所で，「xについて整理する」とは，x2の項，xの項，定数項をまとめることをいう．ここでは特にxの１次の項の係数をまとめて「かっこ」でくくることが重要． ※ この計算で失敗する生徒は，次のようにxの係数を小出しにしてもつれてしまうことが多い： y=2(x2+2ax)+a2−8x−5a+4…（まだ外に- 8xが残っている！)
⇒ xの係数を「かっこ」でくくって，団体ごとまとめて平方完成する．（「♪～パックに詰める～」）
［例題4］ y=−x2+ax+a2+3x−2a+4 ■xについて整理する …★ =−x2+(a+3)x+(a2−2a+4) ■x2の係数でくくる（定数項は後回し) =−{ x2−(a+3)x }+(a2−2a+4) ■{ .. }の中を平方完成する．xの係数の半分を持ってくる． =−{ (x−  a+32)2−(a+32)2}+(a2−2a+4)■外側の{ .. }をはずす =−(x− a+32)2+(a+32)2+(a2−2a+4)■定数項を簡単にして仕上げる =−(x− a+32)2+5a2−2a+254頂点の座標は( a+32,5a2−2a+254)
|
|
［問題2］ 次の２次関数の軸の方程式と頂点の座標を求めよ． (1) y=x2+6ax (2) y=−2x2+8ax+a2+1 (3) y=2x2+4ax+a2−4x+6a+5 (4) y=−x2+3ax+a2−2x+3a+1 |
| 隨�ｿｽ邵ｺ阮呻ｿｽ郢ｧ�ｵ郢ｧ�､郢昜ｺ･�ｽ邵ｺ�ｮGoogle隶諛�ｽｴ�｢隨�ｿｽ |
...�ｽ蝓溷｣ｰ陝ｶ�ｯ霑夊肩�ｼ蟲ｨﾎ鍋ｹ昜ｹ斟礼ｹ晢ｽｼ邵ｺ�ｫ隰鯉ｽｻ郢ｧ�ｽ