次の放物線の形は正式には「下に凸」（下にふくらんでいる）と呼ばれるが，この頁では平凡な日常用語で「谷形」ということにする．
次の放物線の形は正式には「上に凸」（上にふくらんでいる）と呼ばれるが，この頁では平凡な日常用語で「山形」ということにする．
| |
|
《 問題 》 １ 次の２次関数の最大値について正しいものを選びなさい． (1) 
|
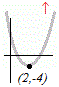
図のように谷形のグラフになるから，限りなく大きな値をとり，最大値はない
|
(2)
|
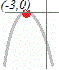
図のように頂点が(−3, 0)の山形のグラフになるから，x=−3のとき最大値y=0となる
|
(3)
|
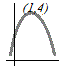
図のように頂点が(1, 4)の山形のグラフになるから，x=1のとき最大値y=4となる
|
(4)
|
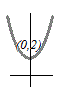
図のように頂点が(0, 2)の谷形のグラフになるから，限りなく大きな値をとり，最大値はない
|
(5)
|
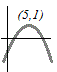
図のように頂点が(5, 1)の山形のグラフになるから，x=5のとき最大値y=1となる
|
|
２ 次の２次関数の最小値について正しいものを選びなさい．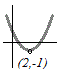 
|
図のように頂点が(2, −1)の谷形のグラフになるから，x=2のとき最小値y=−1となる
|
|
(2)
|
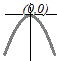
図のように頂点が(0, 0)の山形のグラフになるから，限りなく小さな値をとり，最小値はない
|
|
| (3) ｙ＝－(ｘ－３)2＋４
|
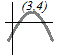
図のように頂点が(3, 4)の山形のグラフになるから，限りなく小さな値をとり，最小値はない
|
|
(4)
|
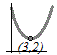
図のように頂点が(3, 2)の谷形のグラフになるから，x=3のとき最小値y=2となる
|
|
(5)
|
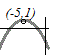
図のように頂点が(−5, 1)の山形のグラフになるから，限りなく小さな値をとり，最小値はない
|
 ...（携帯版）メニューに戻る...（PC版）メニューに戻る
|
|
■［個別の頁からの質問に対する回答］[２次関数の最大値・最小値について／18.6.29］
大問2の答えが偏ってるのが気になりました。
■［個別の頁からの質問に対する回答］[２次関数の最大値・最小値について／17.8.24］
＝＞［作者］：連絡ありがとう．例えば，どの選択肢も同じ頻度で登場するという場合，それはそれで一定の規則に縛られていることになります．このように宝くじのあたり番号で同じ番号が続いてはいけないというルールはないのです． 簡単よー
＝＞［作者］：連絡ありがとう．簡単でも基本なので必ずできるようにしてください |
| 鬮ｫ�ｨ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ鬩搾ｽｵ�ｽ�ｺ鬮ｦ�ｮ陷ｻ�ｻ�ｽ�ｿ�ｽ�ｽ鬩幢ｽ｢�ｽ�ｧ�ｽ�ｽ�ｽ�ｵ鬩幢ｽ｢�ｽ�ｧ�ｽ�ｽ�ｽ�､鬩幢ｽ｢隴乗��ｽ�ｺ�ｽ�･�ｽ�ｽ�ｽ�ｽ鬩搾ｽｵ�ｽ�ｺ�ｽ�ｽ�ｽ�ｮGoogle鬮ｫ�ｶ�つ髫ｲ蟷｢�ｿ�ｽ�ｽ�ｽ�ｽ�ｴ�ｽ�ｽ�ｽ�｢鬮ｫ�ｨ�ｽ�ｽ�ｽ�ｿ�ｽ�ｽ |