← PC用は別頁
|
【例1】
(解答)a>0, b>0, 0≦t≦2πのとき,x=acost , y=bsintで囲まれた図形の面積を求めてください. [曲線の概形を描く] (1) tの変化に対応したx, yの増減を調べる.
=−asint, =bcostだから
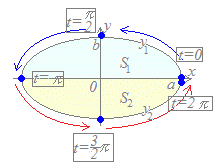 (2) [ y dxの形で面積を表す] 青で示した部分の面積は y1 dx ピンクで示した部分の面積は (−y2)dx 求める図形の面積は S=y1 dx−(−y2 )dx (3) [ 置換積分により変数をtに直して計算する] (被積分関数) : y → bsint (積分変数) : dx=−asintdt (積分区間) :
S=bsint(−asint)dt−bsint(−asint)dt =−absin2dt+absin2dt =absin2dt+absin2dt =absin2dt =abdt =ab−=πab
a=b(=r)のときは,円になり,S=πr2となります.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(参考1)
上の方程式は,楕円 +=1 の媒介変数表示になっています.
(参考2)
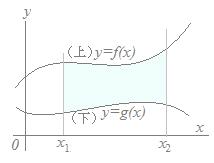 というのは,この問題では(上)と(下)は関数形によって区別されるのではなく,(上)(下)の関数形は同じになるため,単純に引き算をすれば消えてなくなってしまいます. (上)であるか(下)であるかはtの積分区間によって区別されています.だから,上図のようにx軸とで囲まれる図形の面積を2つに分けて計算します. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
【例2】
(解答)a>0のとき,x=a(t−sint) , y=a(1−cost)とx軸とで囲まれた図形の面積を求めてください. [曲線の概形を描く] (1) tの変化に対応したx, yの増減を調べる.
=a(1−cost)≧0, =asintだから
(2) [ y dxの形で面積を表す] S=y dx (3) [ 置換積分により変数をtに直して計算する] (被積分関数) : y → a(1−cost) (積分変数) : dx=a(1−cost)dt (積分区間) :
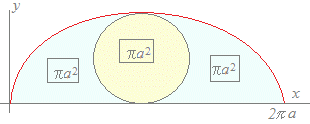 |
||||||||||||||||||||||||||||||||||||||
|
(参考3)
上のグラフはサイクロイドと呼ばれ,円が直線上を滑らずに回転するときに,円周上の1点が描く軌跡となっています. 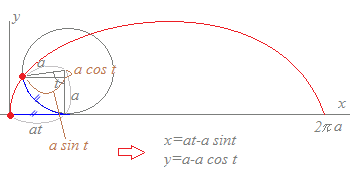 |
|
【問題1】
解説次の途中計算を参考にしてx=sint , y=sin2t(0≦t≦π)で囲まれる図形の面積を求めてください (途中計算) =cost , =0 ⇔ t= =2cos2t , =0 ⇔ t=,
グラフは次のようになる. 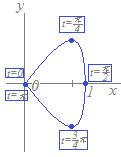 |
||||||||||||||||||||||||||||||||||||||||||||||||||
| 三角関数の公式を使って,積を和に直してから積分します. S=sin2tcost dt ={ sin3t+sint }dt =−−cost ={ (+1)−(−−1) }= |
|
【問題2】
解説次の途中計算を参考にしてx=sin2t , y=sin3t(0≦t≦)で囲まれる図形の面積を求めてください (※暗算ではできません.計算用紙が必要です.) (途中計算) =2cos2t , =0 ⇔ 2t= ⇔ t= =3cos3t , =0 ⇔ 3t= ⇔ t= y=0 ⇔ 3t=0,π ⇔ t=0,π
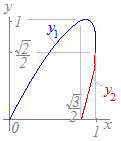 |
||||||||||||||||||||||||||||||||||||||||
| S=y1 dx−y2 dx =sin3t·2cos2t dt−sin3t·2cos2t dt =sin3t·2cos2t dt+sin3t·2cos2t dt =sin3t·2cos2t dt 三角関数の公式を使って,積を和に直してから積分します. S=(sin5t+sint)dt =−−cost ={ (−−)−(−−1) }== |
|
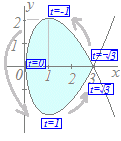
【問題3】x=t2 , y=t3−3tで囲まれる図形の面積を求めてください
解説(※暗算ではできません.計算用紙が必要です.速い人でも10分はかかるでしょう.) =2t , =0 ⇔ t=0 =3t2−3t , =0 ⇔ t=±1 y=0 ⇔ t(t2−3)=0 ⇔ t=0,±
|
||||||||||||||||||||||||||||||||||||||||||||||||||
グラフは次のようになる.
 |
|
[注]直前にPC版から入られた場合は,自動転送でスマホ版に来ていますので,ブラウザの[戻るキー]では戻れません(堂々巡りになる).下記のリンクを使ってメニューに戻ってください.
|