(2)�̂悤�ɐϕ��ϐ���t�ŁC����Ƃ͈قȂ镶��x�Ƃ̑召�ɉ����Đ�Βl�L���̂͂��������l����Ƃ�
t�Őϕ�����Ƃ��́Cx�͒P�Ȃ�萔�Ƃ��Ĉ����C�ł���������x�̎���x�̊��Ƃ��鎖���(1)�Ɠ����ł����Cx���ϕ���Ԃ̒��ɂ���ꍇ�ɂ́C�ꍇ�������Đϕ����邱�ƂɂȂ�܂��D
�y��z
=\int_{0}^1\mid t-x\mid dt\]&chf=bg,s,ffffdd) \( \displaystyle f(x)=\int_{0}^1\mid t-x\mid dt \) \( \displaystyle f(x)=\int_{0}^1\mid t-x\mid dt \)
�� x�̊ȒP�Ȏ��ŕ\���Ă��������D
�i�j
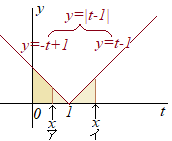
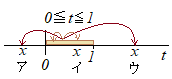 (�A) x<0�̂Ƃ��C�ϕ����0��t��1�Ɋ܂܂��ǂ�t�̒l��t−x>0��������
(�A) x<0�̂Ƃ��C�ϕ����0��t��1�Ɋ܂܂��ǂ�t�̒l��t−x>0��������
=\int_{0}^1\mid t-x\mid dt=\int_{0}^1(t-x)dt\]) \( \displaystyle f(x)=\int_{0}^1\mid t-x\mid dt=\int_{0}^1(t-x)dt \) \( \displaystyle f(x)=\int_{0}^1\mid t-x\mid dt=\int_{0}^1(t-x)dt \)
-(0-0)=\frac{1}{2}-x) \( \displaystyle =\left[\frac{t^2}{2}-xt\right]_0^1=(\frac{1}{2}-x)-(0-0)=\frac{1}{2}-x \) \( \displaystyle =\left[\frac{t^2}{2}-xt\right]_0^1=(\frac{1}{2}-x)-(0-0)=\frac{1}{2}-x \)
x�͒萔������l���Œ肳��Ă���D
x�ɐ�Ɏ���o�����Ă���Ct�́u��o���W�����P���v������
(�C) 0��x<1�̂Ƃ��C�ϕ����0��t��1�Ɋ܂܂��t�̒l�̂���
i) 0��t<x�̂Ƃ��Ct<x������|t−x|=−t+x
ii) x��t��1�̂Ƃ��Ct��x������|t−x|=t−x
=\int_{0}^1\mid t-x\mid dt=\int_{0}^x(-t%2B x)dt%2B\int_x^1(t-x)dt\]&chs=340x48) \( \displaystyle f(x)\!=\!\int_{0}^1\mid \!t\!-\!x\!\mid\! dt\!=\!\int_{0}^x(\!-\!t+\! x)dt\!+\!\int_x^1(t\!-\!x)dt \) \( \displaystyle f(x)\!=\!\int_{0}^1\mid \!t\!-\!x\!\mid\! dt\!=\!\int_{0}^x(\!-\!t+\! x)dt\!+\!\int_x^1(t\!-\!x)dt \)
 \( \displaystyle =\left[-\frac{t^2}{2}+ xt\right]_0^x+\left[\frac{t^2}{2}-xt\right]_x^1 \) \( \displaystyle =\left[-\frac{t^2}{2}+ xt\right]_0^x+\left[\frac{t^2}{2}-xt\right]_x^1 \)
-(\frac{x^2}{2}-x^2)) \( \displaystyle =-\frac{x^2}{2}+ x^2-0+(\frac{1}{2}-x)-(\frac{x^2}{2}-x^2) \) \( \displaystyle =-\frac{x^2}{2}+ x^2-0+(\frac{1}{2}-x)-(\frac{x^2}{2}-x^2) \)
 \( \displaystyle =x^2-x+\frac{1}{2} \) \( \displaystyle =x^2-x+\frac{1}{2} \)
(�E) x��1�̂Ƃ��C�ϕ����0��t��1�Ɋ܂܂��ǂ�t�̒l��t−x��0��������
=\int_{0}^1\mid t-x\mid dt=\int_{0}^1(-t%2B x)dt\]) \( \displaystyle f(x)=\int_{0}^1\mid t-x\mid dt=\int_{0}^1(-t+x)dt \) \( \displaystyle f(x)=\int_{0}^1\mid t-x\mid dt=\int_{0}^1(-t+x)dt \)
 \( \displaystyle =\left[-\frac{t^2}{2}+ xt\right]_0^1=-\frac{1}{2}+ x \) \( \displaystyle =\left[-\frac{t^2}{2}+ xt\right]_0^1=-\frac{1}{2}+ x \)
|
 ��ϕ��̊�{
��ϕ��̊�{
 ��ϕ��̒u���ϕ�
��ϕ��̒u���ϕ�
 ��(2)
��(2) ��ϕ��̕����ϕ�
��ϕ��̕����ϕ�
 �������̒�ϕ�
�������̒�ϕ� �O�p���i��Βl�t���j�̒�ϕ�
�O�p���i��Βl�t���j�̒�ϕ� lim���ƒ�ϕ��̊W
lim���ƒ�ϕ��̊W
 �Ȑ��ň͂܂ꂽ�}�`�̖ʐ�
�Ȑ��ň͂܂ꂽ�}�`�̖ʐ�
 ��(2)�}��ϐ�
��(2)�}��ϐ�
 ��(3)
��(3)
 ��ϕ��̑Q����
��ϕ��̑Q����
 �Ȑ��̒���
�Ȑ��̒��� ��]�̂̑̐�
��]�̂̑̐�
 �L�`�ϕ�
�L�`�ϕ�
 �d�ϕ�
�d�ϕ�
 �ȒP�ȏd�ϕ��̌v�Z
�ȒP�ȏd�ϕ��̌v�Z �ϕ��̈悪�ϐ��Ɉˑ�����ꍇ�̏d�ϕ�
�ϕ��̈悪�ϐ��Ɉˑ�����ꍇ�̏d�ϕ� �ϕ������̕ύX
�ϕ������̕ύX
 �ϐ��ϊ��F���R�r�s��
�ϐ��ϊ��F���R�r�s��


 �@
�@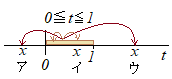 (�A)
(�A)