|
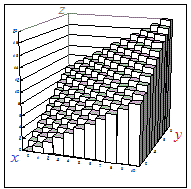
���}�P�̂悤�ȗ��̂̑̐ρi�c�_�̑̐ς̑��a�j�́C�ʐϗv�fds=dxdy�ɍ���z=f(x, y)���|���ē�����̐ϗv�f
dV=f(x, y)ds=f(x, y)dxdy �̑��a�Ƃ��āC��`��D��̏d�ϕ� f(x, y)dxdy �ŋ��߂邱�Ƃ��ł��܂��D
�}�P
��f(x, y)���A�����ŁC�e�ϐ��̒�`�悪a��x��b, ����y�����ł���Ƃ�,���̏d�ϕ���
 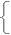 f(x, y)dx f(x, y)dx 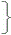 dy…(1) dy…(1)�܂��� 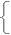 f(x, y)dy f(x, y)dy 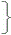 dx…(2) dx…(2)�̂悤�ɁC�P�ϐ��̐ϕ��̌J��Ԃ��ɂ���čs�����Ƃ��ł��܂��D �@(1)�͐}�Q�̂悤�ɁC�܂��ϐ�y���Œ肵�āC�e�X��y�ɂ��āCx�Őϕ����i�}�Ŏ������ǂ̖ʐ�S(y)�����߂āj�C����y�̊��Ƃ��ĕ\���ꂽ���̖ʐς�y�Őϕ����邱�Ƃɂ���đ̐ς����߂邱�ƂɑΉ����Ă��܂��D
�}�Q
 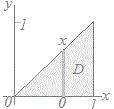 �@(2)�͐}�R�̂悤�ɁC���߂�x���Œ肵��y�Őϕ����C�}�Ŏ������ǂ̖ʐ�S(x)�����߂āC����x�Őϕ�������̂ł��D
�@(2)�͐}�R�̂悤�ɁC���߂�x���Œ肵��y�Őϕ����C�}�Ŏ������ǂ̖ʐ�S(x)�����߂āC����x�Őϕ�������̂ł��D
�}�R
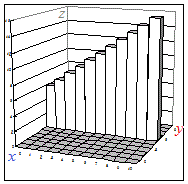 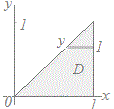 ���ϐ��̒�`�悪0��x��1, 0��y��x�̂悤�ɑ��̕ϐ��Ɉˑ����Ă���Ƃ���
���ϐ��̒�`�悪0��x��1, 0��y��x�̂悤�ɑ��̕ϐ��Ɉˑ����Ă���Ƃ���
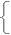 f(x, y)dy f(x, y)dy 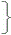 dx dx
�܂���0��y��1, y��x��1�Ƃ��� 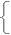 f(x, y)dx f(x, y)dx 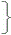 dy dy�̂悤�Ɍv�Z�ł��܂��D
�y��{�̊m�F�z
(1) kx dx �̂悤��dx�̕����Ŏ�����Ă���ϕ��ϐ�x�ȊO�̕����ik�j�́C�萔�Ƃ݂Ȃ��܂��D������C���̐ϕ��� kx dx=k× =−0=�ɂȂ�܂��D (2) yx dx �̏ꍇ���Cy��x�ƓƗ��ȕϐ��ł������C���l�ɂ��� yx dx=y× =�ɂȂ�܂��D
���̌��ʂ́Cy�̊��ɂȂ�̂ŁC�u���̒i�K�Ƃ���y�ɂ��Đϕ�����v�Ƃ����悤�Ȃ��Ƃ��ł��܂��D
dy==1
������
(yx dx)dy=()dy= =1
�ƂȂ�܂��D
(3) �ϕ��ϐ���y�ł���Ƃ��C�Ⴆ��
xy dy
�̏ꍇ�́C���x��dy�̕����Ŏ�����Ă���ϕ��ϐ�y�ȊO�̕����ix�j�́C�萔�Ƃ݂Ȃ��܂��D������C���̐ϕ���
xy dy=x× =2x
�ɂȂ�܂��D
���̌��ʂ́Cx�̊��ɂȂ�̂ŁC�u���̒i�K�Ƃ���x�ɂ��Đϕ�����v�Ƃ����悤�Ȃ��Ƃ��ł��܂��D
2x dx=x2=1
������
(yx dy)dx=(2x)dx=x2=1
�ƂȂ�܂��D
|
|
�y����̖�肪�܂܂�鏑�Ёz
�u�����ϕ��w�U�v�i�����o�� ��b���w�u���V��/�F�엘�Y���j �u�V�� ����̐��w�R ���W�v�i�X�k�o��/�c��ÍG���j �u���H�n��b �����ϕ��w�v�i�|����/�x�������Y.���A�g.�Y������Y�����j �u���w�ւ̃A�v���[�`�v�i�։ؖ[/���؍��ߒ��j
�i�Q�l�j
(*1)�@y=x2�̂Ƃ�y dx�����߂� �Ƃ����悤�Ȗ��ɂ����ẮCy��x�̊��ɂȂ��Ă���x�ƓƗ��ȕϐ��ł͂���܂���D������C y dx=yx=2y ←�ԈႢ y dx=x2 dx= = ←������ (*)�@�L�� (yx dy)dx��
yx dydx�Ƃ�������܂��D
�܂��C0��y��2, 0��x��1�̗̈��D�ŕ\���Ƃ�
���̏ꍇ�C�e�X�̐ϕ���Ԃ�0��y��2, 0��x��1�ƂȂ�܂��D
yx dydx�Ƃ�������܂��D
����ɁC
yx dydx��dxyx dy
�Ə������Ƃ�����܂��D���̏ꍇ�C�ϐ�x�ɂ��Đϕ�����Ƃ��̔�ϕ����́C��O�I��dx�̉E�ɏ�����Ă��邱�ƂɂȂ�܂��D
�y�v�_�z
�@���̊e�L���́C��������̈�D : c��y��d, a��x��b�ɂ����āC�͂��߂�y�ŁC����x�Őϕ����邱�Ƃ�\���D (f(x,y)dy)dx , f(x,y)dydx dxf(x,y)dy , f(x,y)dydx |