曲線の長さ

【公式】
○媒介変数表示で表される曲線x=f(t) , y=g(t)の区間α≦t≦βにおける曲線の長さは
$L=\int_\alpha^\beta$ $\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt$

○x ,y直交座標で表される曲線y=f(x)の区間a≦x≦bにおける曲線の長さは
$L=\int_a^b$ $\sqrt{1+\left(\frac{dy}{dx}\right)^2}dx$

○極座標で表される曲線r=f(θ)の区間α≦θ≦βにおける曲線の長さは
$L=\int_\alpha^\beta$ $\sqrt{r^2+\left(\frac{dr}{d\theta}\right)^2}d\theta$
※極座標で表される曲線の長さの公式は，高校向けの教科書や参考書には掲載されていないが，媒介変数表示で表される曲線と解釈すれば解ける．（［→例］）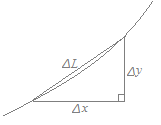

（解説）

　ピタグラスの定理（三平方の定理）により，横の長さがΔx，縦の長さがΔyである直角三角形の斜辺の長さΔLは
$\Delta L=\sqrt{(\Delta x)^2+(\Delta y)^2}$
したがって
$\frac{\Delta L}{\Delta t}=\sqrt{\left(\frac{\Delta x}{\Delta t}\right)^2+\left(\frac{\Delta y}{\Delta t}\right)^2}$
$\frac{dL}{dt}=\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}$
$L=\int_\alpha^\beta$ $\sqrt{\left(\frac{dx}{dt}\right)^2+\left(\frac{dy}{dt}\right)^2}dt$

○x ,y直交座標ではx=tとおけば上記の公式が得られる．
$\frac{dx}{dt}\rightarrow \frac{dx}{dx}=1, \frac{dy}{dt}\rightarrow \frac{dy}{dx}, td\rightarrow dx$ により
$L=\int_a^b$ $\sqrt{1+\left(\frac{dy}{dx}\right)^2}dx$

図で言えば $dL^2=(dx)^2 + (y'dx)^2$ だから
$dL=\sqrt{1 + (y')^2}dx$

$L=\int_a^b\sqrt{1 + (y')^2}dx$

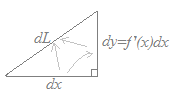○極座標でr=f(θ)のとき，媒介変数をθに選べば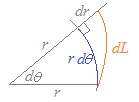

$x=r\cos \theta=f(\theta)\cos \theta$
$y=r\sin \theta=f(\theta)\sin \theta$

となるから

$\frac{dx}{d\theta}=f'(\theta)\cos \theta + f(\theta)(-\sin \theta)$
$\frac{dy}{d\theta}=f'(\theta)\sin \theta + f(\theta)\cos \theta$

$\left(\frac{dx}{d\theta} \right)^2+\left(\frac{dy}{d\theta} \right)^2$
$=f'(\theta)^2\cos ^2\theta -2 f'(\theta)f(\theta)\sin \theta\cos \theta + f(\theta)^2 \sin ^2\theta$
$+f'(\theta)^2\sin ^2\theta + 2f'(\theta)f(\theta)\sin \theta\cos \theta + f(\theta)^2 \cos ^2\theta$
$=f'(\theta)^2 + f(\theta)^2=r^2 + f'(\theta)^2$
$L=\int_\alpha^\beta$ $\sqrt{r^2+\left(\frac{dr}{d\theta}\right)^2}d\theta$

極座標でrが一定ならば，弧の長さはdL=rdθで求められるが，一般にはrも変化する．
そこで， $dL=\sqrt{(rd\theta)^2+(dr)^2}$
$=\sqrt{r^2+(\frac{dr}{d\theta})^2}\cdot d\theta$ の形になる

次の項目