|
|
|
|
|
問題次の曲線の長さを求めてください. 2 4 π 2π 4π
(上記の範囲では (参考) この問題は,x , y座標で与えられた方程式から曲線の長さを求める問題なので,上記のように答えてもらえばOKです. 図形的には,円x2+y2=4 (x≧2 , y≧2)のうちのx≧0 , y≧0の部分なので,半径2の円のうちの第1象限の部分の長さ:2π×2÷4=πになります. [高校の範囲で解いた場合]
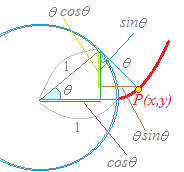
x=rcosθ=2sinθcosθ=sin2θ
として,媒介変数表示の場合の曲線の長さを求めるとよい.y=rsinθ=2sinθsinθ=1−cos2θ
(∵)cos2θ=1−2sin2より
2sin2θ=1+cos2θ ここで三角関数の2倍角公式により だから また三角関数の相互関係から (2)(3)を(1)に代入すると だから [高校の範囲で解いた場合]
x=rcosθ=(1+sinθ)cosθ=cosθ+sinθcosθ
として,媒介変数表示の場合の曲線の長さを求めるとよい.y=rsinθ=(1+sinθ)sinθ=sinθ+sin2θ となり(1)以下同様になる. (参考) だから,このグラフはカージオイド カージオイド |
 (参考)
(参考)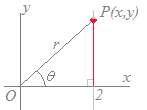 (参考)
(参考)