← PC用は別頁
|
*** 科目 *** 数Ⅰ・A数Ⅱ・B数Ⅲ高卒・大学初年度 *** 単元 *** 数と式不等式二次関数二次不等式三角比三角比と図形集合・命題・証明順列・組合せ確率整数の性質 ※高校数学Aの場合の数・順列・組合せについて,このサイトには次の教材があります.
この頁へGoogleやYAHOO ! などの検索から直接来てしまったので「前提となっている内容が分からない」という場合や「この頁は分かったがもっと応用問題を見たい」という場合は,他の頁を見てください. が現在地です. ↓積の法則 ↓和の法則 ↓場合の数のまとめ方 ↓樹形図,辞書式配列 ↓階乗 ↓階乗・順列 ↓隣り合う.合わない並び方  ↓両端指定・整数の順列 ↓円順列・じゅず順列 ↓重複順列 ↓組合せ ↓組合せ(2) ↓組合せ(文章題) ↓組分け ↓同じものがあるときの順列 ↓順路の問題 ↓番号札のもらい方 ↓二項定理,多項定理 ↓重複組合せ ↓重複組合せ(文章題) 順列,組合せ(章末問題) |
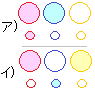 左端は6通り.2番目は同色以外の4通り.(6×4)
左端は6通り.2番目は同色以外の4通り.(6×4)