�@�j �����������ɂȂ�Ƃ�
�@�s��̐����̂�������������ɂȂ�Ƃ��CExcel�̏����ݒ�̂܂����\���i�܂��͎w���\���j�ɂ��Ă����ƁC�ǂ̂悤�ȕ�����\�킵�Ă���̂��悭������Ȃ����Ƃ�����D
�@���̂Ƃ��C�\���`���Ƃ��āu�����v��I�ԂƁC�����Ƃ��ĕ\���ł���D
�� ����������̏ꍇ���C���q�̕�����������傫�������ƂȂ�ꍇ�́C�������ł͂Ȃ��ѕ����ŕ\�������D
�� �����������̌`�̕����ŁC���ꂪ3���ȉ��̐����ŕ\����ꍇ�́C(A)(B)(C)�̂�����ōs���Ă��C�������ʂ�������D�������C(C)�ł́C# ???/???�����ł́C�}�C�i�X�̕�����\���Ȃ��̂Œ��ӥ��(A)(B)�ƈႤ
�� �����������̌`�̕����ŁC���ꂪ4���ȏ�i�Ƃ����Ă����ۏ��6, 7���ȓ��j�̐����ŕ\����ꍇ�́C(B)�ł�3���܂ł̋ߎ������ŕ\�������D(A)(C)�ł͕���̌�����傫���ł��邪�C����ł��Ȃ��C���m�Ȓl���������ɋߎ��l�ƂȂ�Ƃ��́C(C)�̕����ŗNjߎ������ƂȂ邱�Ƃ������D
�m�菇�n
(A)(B)�̏ꍇ
�t�s������炩���ߋ��߂Ă����D�������\���ɂ������Z�����h���b�O���Ĕ��]�\���ɂ���
���������Z�����i�\���`���j���ށF�����C��ށF3���������n�j
�@(A)PC�ɃC���X�g�[�����Ďg��Excel��(B)Excel Online�Ő��l�̕����\����I�ԂƂ��u1�������v�u2�������v�u3�������v�Ƃ���������I�Ԃ��ƂɂȂ邪�C���́u�����v�͂��Ԃ���Łu1���܂Łv�u2���܂Łv�u3���܂Łv�Ƃ����Ӗ��ł���D
���ꂪ3���܂ł̐�����Ƃ��镪���ł͕\���ł��Ȃ��Ƃ��C�i4���C5���C������K�v�ȏꍇ�j
(B)�̏ꍇ
3���܂ł̋ߎ������ɂȂ�
�y��z
| �@ |
A |
B |
C |
D |
E |
F |
| 1 |
9 |
10 |
23 |
37/442 |
−50/237 |
37/245 |
| 2 |
11 |
19 |
17 |
−21/221 |
73/442 |
−25/442 |
| 3 |
17 |
21 |
11 |
23/442 |
1/93 |
−1/29 |
�Z���̏����ݒ�→�\���`��→���[�U�[��`�F��ނ��菑���ŏ��������� # ????/???? �Ƃ����4���܂ŁC# ?????/????? �Ƃ����5���܂ŁC����ƕ\��������ύX�ł���D�i4���܂łŎ��̕\�̂悤�ɂȂ�j
| �@ |
A |
B |
C |
D |
E |
F |
| 1 |
9 |
10 |
23 |
37/442 |
−373/1768 |
267/1768 |
| 2 |
11 |
19 |
17 |
−21/221 |
73/442 |
−25/442 |
| 3 |
17 |
21 |
11 |
23/442 |
17/1768 |
−61/1768 |
�\���`��→����→�J�X�^���\���`���F�菑���ŏ��������� # ????/????;-# ????/???? �Ƃ����4���܂ŁC# ?????/?????;-# ?????/????? �Ƃ����5���܂ŁC����ƕ\��������ύX�ł���
�i�Z�~�R�����ŋ���āC���̏ꍇ -# ????/????��lj�����K�v������D�����ӂ�ƁC�}�C�i�X�̏ꍇ�ɕ������\������Ȃ��j
4���܂ł�(A)�̕\�Ɠ����ɂȂ�D
�ߎ������Ɋւ��āCExcel��Google�X�v���b�h�V�[�g�̑���_�ɂ��āC�M�ʂ̍l���́C �˂��̃y�[�W�̌㔼�ɂ܂Ƃ߂Ă���܂��D
|
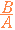 ��
�� 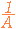 �Ƃ����L�����g�����ł͂Ȃ��D�܂��CA2 , A3 , ... �Ȃǂ͒�`����Ă��邪�CA−2 , A−3 , ... �Ȃǂ̈Ӗ��������I�ɒ�܂�킯�ł͂Ȃ��D�iA2 , A3 , ...�̋t�s��Ȃ̂��CA−1�̂Q��C�R��C...�Ȃ̂��j�����ł́C�t�s��̋L�� −1 �́C�t�s���p�́u�t�́v�Ƃ����L���Ƃ��Ďg���D
�Ƃ����L�����g�����ł͂Ȃ��D�܂��CA2 , A3 , ... �Ȃǂ͒�`����Ă��邪�CA−2 , A−3 , ... �Ȃǂ̈Ӗ��������I�ɒ�܂�킯�ł͂Ȃ��D�iA2 , A3 , ...�̋t�s��Ȃ̂��CA−1�̂Q��C�R��C...�Ȃ̂��j�����ł́C�t�s��̋L�� −1 �́C�t�s���p�́u�t�́v�Ƃ����L���Ƃ��Ďg���D
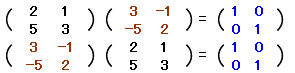
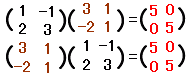
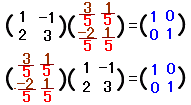
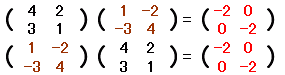
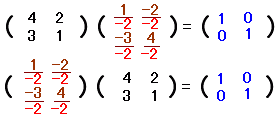
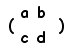 �̋t�s��́C
�̋t�s��́C
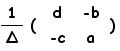



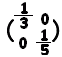
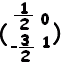

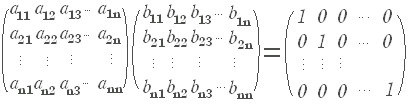 ���@���~���s��ɂ��Ă͋t�s��̗L�����l���邱�Ƃ��ł��܂��D�����s��łȂ���t�s����l����]�n�͂���܂���D
���@���~���s��ɂ��Ă͋t�s��̗L�����l���邱�Ƃ��ł��܂��D�����s��łȂ���t�s����l����]�n�͂���܂���D