|
(参考)…数の場合の単位元の定義
任意の数xに対して右から掛けても左から掛けてもその値を変えない数を単位元という.
数の単位元eは1である.すなわち,次の等式が成り立つ.
※ 単位元は,すべての数に対して共通なものが1つだけある.(e=1) ○ 単位行列の定義
任意のn次正方行列Aに対して右から掛けても左から掛けてもAとなるような行列を単位行列という.
※ 単位行列は次数ごとに決まる.紛らわしくなければ,単にEで表してもよいが,次数の異なる様々な単位行列を扱っているときは,その次数に応じてEnで表す.
2次の単位行列はE2=
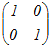
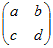 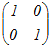 = =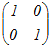 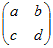 = =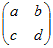
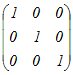
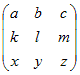 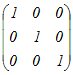 = =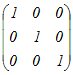 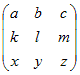 = 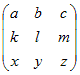
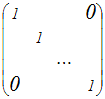
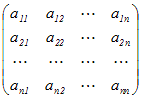 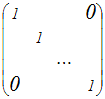 = 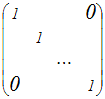 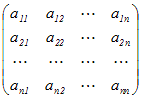 = 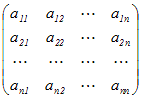
|
|
(参考)…数の場合の逆元の定義
各々の数x (x≠0)に対して右から掛けても左から掛けても単位元となる数yをxの逆元という.
ある.すなわち,次の等式が成り立つ.
例 2の逆元は,3の逆元は ○ 逆行列の定義
与えられたn次正方行列Aに対して右から掛けても左から掛けても単位行列Eとなるような行列をAの逆行列といい,A−1で表す.
逆行列の例
A= 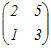 のとき のとき
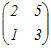 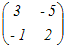 = =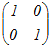 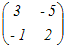 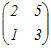 = =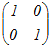
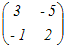 B=
B=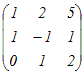 のとき のとき
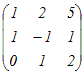 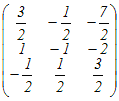 = =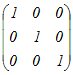 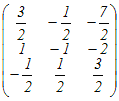 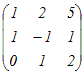 = =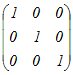
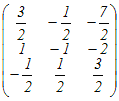 ※ 行列の割り算は定義されていないので 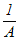 とは書かない.ここでは,−1という記号を「逆の」という意味の記号だと考えるとよい. とは書かない.ここでは,−1という記号を「逆の」という意味の記号だと考えるとよい.※ 逆行列は,正方行列に対してのみ定義でき,正方行列でない行列に対しては逆行列は考えない. また,0でない数に対してのみ逆数があるのと同様の事情があり,下記に述べるように行列式が0とならない行列に対してのみ逆行列が存在する.
逆行列が存在する行列は正則であるという.(このような行列を正則行列という.)
|
|
○ 逆行列の求め方(1) Excelで求める方法
下の表1においてA1:D4に4×4行列が入力されているとき,その逆行列をF1:I4に書き込む場合を例にとって解説する.
Excelのワークシート関数で逆行列を求めるものは MINVERSE(元の行列の範囲) なので,これを利用する.
1) セルF1に =MINVERSE(A11:D14) と書きこむ. (関数を覚えずにメニューからたどっていくときは,画面上の方にある数式バーの左側のfxをクリック→関数の分類:数学/三角またはすべて,関数名:MINVERSE OK →配列:A1:D4 OK) 2) 1)の段階ではF1のセルに逆行列の1つの成分が書き込まれるだけで逆行列全体(配列=行列)が書き込まれるわけではない.そこで,次に逆行列全体を得るために,F1:I4の範囲を配列にする.そのためには, F1:I4の範囲を選択,反転表示にしておいて,画面上の数式バーをポイントし,Ctrl+ShiftしながらEnterを押す. *) 下記の表1の例のように,元の行列Aの各成分が整数値であってもその逆行列の各成分は小数(または分数)となることが多い.Excelでセルの書式設定が「標準」や「数値」になっているとどのような分数を表しているのか分からないことがある.
(i) 分母が3桁までの分数になるときは,下記のように分数で表示することができる.このとき,負の分数は帯分数として表示され,整数部分にのみ符号が付けられる.例 -3 1/3 = -10/3 のこと
Excel2002:書式→セル,分数,3桁増加 Excel2007:ホーム→セル 書式,分数,3桁増加 (ii) 元の行列の各成分が整数であるのに,分母が4桁以上の分数になるようなときは,後に述べるように逆行列の計算においてdet(A)で割ることが原因なので,得られた逆行列の各係数をdet(A)倍してみると,それがどのような分数を表していたかが分かる.(結果は戻して考える必要あり.注↓)
表1の例では,det(A)=6となり,
例 次の行列の逆行列を求めよ.(各成分は小数第3位まで求めよ.) (1)
(1)
|
|
○ 逆行列の求め方(2) 余因子行列を用いて筆算で求める方法
(解説)
(各成分が数値として与えられた行列の行列式を求めるには1)のExcelによる方法で十分である.
【もとになる定理】線形代数の教科書では行列の「基本変形」を用いて逆行列を求めることが多いが,その説明はかなり長くなるので,ここでは次の定理によって説明する.) 行列Aの余因子行列を よって, 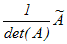
(1) 元の行列の各成分aijに対して,その行と列を取り除いた行列の行列式を求め,これに符号を付ける.(符号までつけたものが余因子Aij)
(2) (1)で求めたものAijを成分とする行列を作る. (3) (2)でできた行列の転置行列を作る.(これが余因子行列 (4) 余因子行列 ◇余因子とは◇ ○ 各(i,j)成分に対して,i行とj列を取り除いた残りの行列を考える. --------------------------------------- (1) 例えばa11に対しては,次のようにa22〜a33の2×2行列を考える.
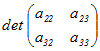 に(−1)1+1の符号を付けたものを(1,1)余因子といいA11で表す. に(−1)1+1の符号を付けたものを(1,1)余因子といいA11で表す.
A11=+
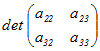 を(1,1)余因子という. を(1,1)余因子という.
--------------------------------------- (2) 同様にして,a21に対しては,次のようにa12〜a33の2×2行列を考える.
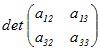 に負の符号を付けたものが(2,1)余因子となる. に負の符号を付けたものが(2,1)余因子となる.
A21=−
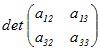 を(2,1)余因子という. を(2,1)余因子という.
(3) a31についても同様にa12〜a23の2×2行列を考える.
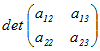 に正の符号を付けたものが(3,1)余因子となる. に正の符号を付けたものが(3,1)余因子となる.
A31=+
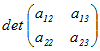 を(3,1)余因子という. を(3,1)余因子という.
◇符号一覧表◇
次の表のように(1,1)成分からスタートして各(i,j)成分に符号を付ける.・・・式では(−1)i+jと書かれるが,結果は「左上端が+のチェック模様」になる. 水色で示したのは第1列に関して余因子展開するときに使う符号
|
|||||||||||||||||||||||||||||||||||||||||||
|
○ 行列Aの行列式det(A)は,これらの余因子を用いて表すことができる.(余因子展開) det(A) =a11· 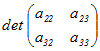 −a21· −a21·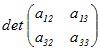 +a31· +a31·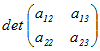
det(A)=a11·A11+a21·A21+a31A31
ここでは行列Aの第1列について展開した余因子展開で示したが,余因子展開はいずれかの列または行について,「行列の成分とその余因子の積の和」を求めたものとなっている.→ これは,行列式が2つのベクトルの内積で表されることを示している. → 行列Aの行列式det(A)はベクトル(a11, a21, a31 )とベクトル(A11, A21, A31 )の内積に等しい. → これは,行ベクトルと列ベクトルの行列としての積が行列式det(A)に等しいことを表している. 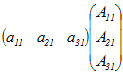 =det(A) …(1) =det(A) …(1)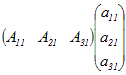 =det(A) …(2) =det(A) …(2)◇余因子行列とは◇ 行列Aの余因子をそのまま並べた行列と行列Aとの積では,上記のような余因子展開に対応するものができない. 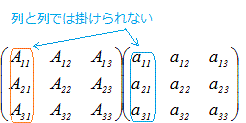  …(3) …(3)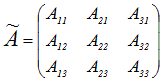 ◇ 1) 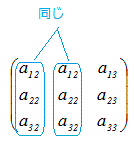
a12·A11+a22·A21+a32A31=0 以上の1)2)をまとめると上記の(3)のようになり
対角成分はdet(A)に等しい.
したがって,
対角成分以外の成分は0に等しい. 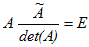
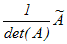 |
|
例1 次の行列の逆行列を求めよ.
(解答)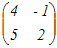 各成分の余因子を求める.
a11=4の余因子はA11=2
行列a12=−の余因子はA12=−5 a21=−の余因子はA21=−(−1)=1 a22=−の余因子はA22=4 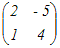 の転置行列が余因子行列 の転置行列が余因子行列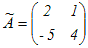 これをdet(A)=4 · 2−5·(−1)=13で割ると 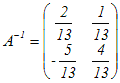 …(答) …(答) |
|
例2 次の行列の逆行列を求めよ.
(解答)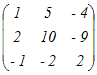 各成分の余因子を求める.(個々の余因子は2×2行列の行列式det(A)=ad−bcに符号を付けたものになる)
a11=1の余因子は10·2−(−2)·(−9)=2
行列a12=5の余因子は−{ 2·2−(−1)·(−9) }=5 a13=−4の余因子は2·(−2)−(−1)·10=6 a21=2の余因子は−{ 5·2−(−2)·(−4) }=−2 a22=10の余因子は1·2−(−1)·(−4)=−2 a23=−9の余因子は−{ 1·(−2)−(−1)·5 }=−3 a31=−1の余因子は5·(−9)−10·(−4)=−5 a32=−2の余因子は−{ 1·(−9)−2·(−4) }=1 a33=2の余因子は1·10−2·5=0 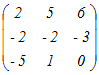 の転置行列が余因子行列 の転置行列が余因子行列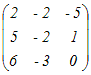 これをdet(A)=1(20−18)−2(10−8)+(−1)(−45+40)=2−4+5=3で割ると 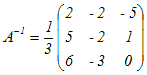 …(答) …(答) |