|
�y�͂��߂Ɂz ���@�s��́C���̗v�f�̌������̓Ɨ������v�f���琬�肽���Ă���C���̂悤�� [�@] ��(�@)�ň͂�ŕ\���܂��D
�y�s�̋��ߕ��z ���@�s�̒l�����̂悤�ɒ�߂闝�R�ɂ��Ă͏ȗ����āC�����ł͌��_�������܂Ƃ߂Ă����܂��D
��2���̍s�̒l�����́C���Z�ł��K���̂Ŋo���Ă����̂����ʂł�
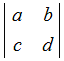 =ad−bc =ad−bc�y��z�@���̍s�̒l�����߂Ă��������D
(1)�@�@
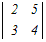
���@�Ⴆ�C�P��ځi�c�j�ɉ����ēW�J����ƌ��߂�D
���@2�ɂ͐��̕������C3�ɂ͕��̕�����t����D 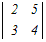 =2×4−3×5=8−15=−7 =2×4−3×5=8−15=−7
(2)�@�@
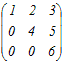
���@0 �������܂܂��s���ɉ����ēW�J����ƌv�Z���y�ɂȂ�܂��D�����ł́C�P��ڂɉ����ēW�J���܂��D
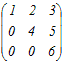 =1× =1×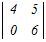 −0+0=24−0=24 −0+0=24−0=24
(3)�@�@
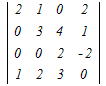
���@0 �������܂܂��s���ɉ����ēW�J����ƌv�Z���y�ɂȂ�܂��D�����ł́C�P��ڂɉ����ēW�J���܂��D
���@4���̍s��←3���̍s��←2���̍s�̂悤�Ɏ����������Čv�Z���܂��D 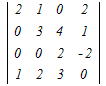 =2 =2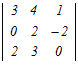 −0+0− −0+0−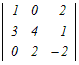 =2(3 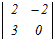 −0+2 −0+2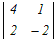 ) )−( 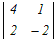 −3 −3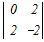 +0) +0)=2{3×6+2(−8−2)}−{(−8−2)−3×(−4)} =2{18−20}−{−10+2}=−4−2=−6
(4)�@�@
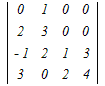
���@0 �������܂܂��s���ɉ����ēW�J����ƌv�Z���y�ɂȂ�܂��D�����ł́C�P�s�ڂɉ����ēW�J���܂��D
���@4���̍s��←3���̍s��←2���̍s�̂悤�Ɏ����������Čv�Z���܂��D 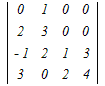 =0− =0−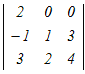 +0−0 +0−0����ɁC�P�s�ڂɉ����ēW�J����̂��L�� =−(2 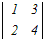 −0+0)=−2(4−6)=4 −0+0)=−2(4−6)=4 |
|
�����̕łɓo�ꂷ��y���z�́C���v�Вc�@�l���{�Z�p�m��̃z�[���y�[�W�Ɍf�ڂ���Ă���u�Z�p�m��ꎟ�����ߋ���� ���ʉȖ�A ���w�v�̈��p�ł��D�i=���\���ꂽ���앨�̈��p�j
���y����z�͌l�̎��Ăł����C�v�������މ��ɂ������āu���̓]�L�~�X�v�u�l�����̊ԈႢ�v�u�v���O�����̍쓮�~�X�v�Ȃǂ��܂܂��ꍇ�����蓾�܂��D �@�������ɂ��Ă̎��ⓙ�́C������҂�ς킹�邱�ƂȂ��C���v�������ނ̍쐬�ҁi<���>�j�ɑ��čs���Ă��������D
0�������܂܂��1��ڂɉ����ēW�J����
0− 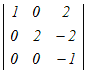 +0−0 +0−0����ɁC0�������܂܂��P��ڂɉ����ēW�J���� =− 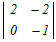 =−(−2−0)=2 → 3 =−(−2−0)=2 → 3
|
|
1��ڂɉ����ēW�J����
x 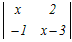 + +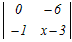 +0 +0=x(x(x−3)+2)+(0−6) =x(x2−3x+2)−6 =x3−3x2+2x−6=0 ���̂R�������������������ɂ���ĉ��� x2(x−3)+2(x−3)=0 (x2+2)(x−3)=0 �������� x=3 → 3 |
|
����18�N�x�Z�p�m��ꎟ�������m���ʖ��n
�y���w�z�V-18 �@�@�@������ 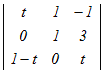 =0����t�̒l�́C���̂ǂꂩ�D =0����t�̒l�́C���̂ǂꂩ�D1−2 2−1 30 41 52 ���
1��ڂɉ����ēW�J����
t 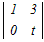 −0+(1−t) −0+(1−t)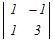 +0 +0=t(t−0)+(1−t)(3+1) =t2−4t+4=0 ����2�������������������ɂ���ĉ��� (t−2)2=0 t=2 → 5 |
|
1��ڂɉ����ēW�J����
0−4 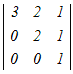 +0−0 +0−0����ɁC1��ڂɉ����ēW�J���� =−4(3 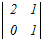 −0+0) −0+0)=−12(2−0) =−24 → 1 |
|
����21�N�x�Z�p�m��ꎟ�������m���ʖ��n
�y���w�z�V-18 �@�@�@�R���s�ɂ���`���������� 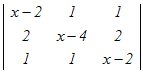 =0�̉��́C���̂ǂꂩ�D =0�̉��́C���̂ǂꂩ�D1−5, 0, 3 2−3, 0, 3 30, 3, 5 41, 3, 5 52, 3, 5 ���
1��ڂɉ����ēW�J����
(x−2) 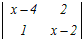 −2 −2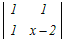 + +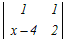 =0 =0=(x−2)(x2−6x+8−2)−2(x−2−1)+(2−(x−4)) =(x−2)(x2−6x+6)−2(x−3)+(−x+6)) =x3−8x2+18x−12−2x+6−x+6 =x3−8x2+15x=0 ���������ɂ���ĉ��� x(x2−8x+15)=0 x(x−3)(x−5)=0 x=0, 3, 5 → 3 |
|
����22�N�x�Z�p�m��ꎟ�������m���ʖ��n
�y���w�z�V-17 �@�s�ɂ��^�����鎮 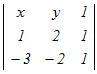 =0�́C���̂ǂ̒�����\�����D =0�́C���̂ǂ̒�����\�����D1x−y+1=02x+y+1=0 3x−y−1=0 4x+y−1=0 5x+y=0 ���
1��ڂɉ����ēW�J����
x 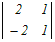 − −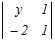 +3 +3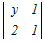 =0 =0x(2+2)−(y+2)−3(y−2)=0 4x−y−2−3y+6=0 4x−4y+4=0 x−y+1=0 → 1 |
|
�P����ɉ����ēW�J����
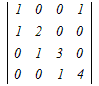 = =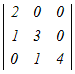 − −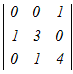 +0−0 +0−0�e�X�̂R���s�Ꭾ���P�s���ɉ����ēW�J���� =2( 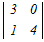 −0+0)−(0−0+ −0+0)−(0−0+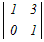 ) )=2(12−0)−(1−0) =24−1=23 → 4 |
|
����24�N�x�Z�p�m��ꎟ�������m���ʖ��n
�y���w�z�V-17 �@�s�ɂ��^����������� 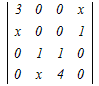 =0�̎��R���̉��́C���̂ǂꂩ�D =0�̎��R���̉��́C���̂ǂꂩ�D11 22 33 44 55 ���
�P����ɉ����ēW�J����
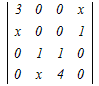 =3 =3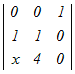 −x −x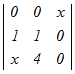 +0−0=0 +0−0=0�e�X�̂R���s�Ꭾ���P�s���ɉ����ēW�J���� 3(0−0+ 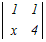 )−x(0−0+x )−x(0−0+x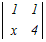 )=0 )=03(4−x)−x(x(4−x))=0 12−3x−4x2+x3=0 x3−4x2−3x+12=0 ���̂R�������������������ɂ���ĉ��� x2(x−4)−3(x−4)=0 (x−4)(x2−3)=0 x=4, ± ���R������ x=4 → 4 |
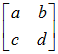
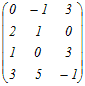
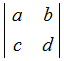
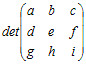
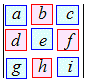
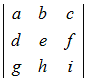 =a
=a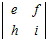 −d
−d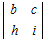 +g
+g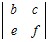
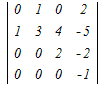 �̒l�́C���̂ǂꂩ�D
�̒l�́C���̂ǂꂩ�D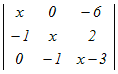 =0
=0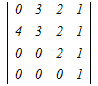 �̒l�́C���̂ǂꂩ�D
�̒l�́C���̂ǂꂩ�D