|
≪行列を対角化するには≫
○ この頁ではn次正方行列Aが相異なるn個の実数の固有値をもつ場合のみを扱う.
○ 統計で登場する相関行列や分散共分散行列などの重要な行列の固有値は実数になる.数学的な理論の上では固有値が等しいという場合もあり得るが,観測データ(実数=小数)を元に実際の作業を行うときに小数の固有値が等しいことはほとんど起こらない. ※ 固有方程式が虚数解をもつ場合や重解をもつ場合の取り扱いは,ややこみいったものになる.これらは,線形代数の教科書・問題集や他のWeb教材に記載されており,この頁では取り扱っていない.
【要点1】
n次正方行列Aが相異なるn個の実数の固有値λ1 , λ2 , …, λn およびこれに対応する固有ベクトル , , ···, をもつとき, 列ベクトル , , ···, を束にした行列をPとおくと, 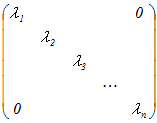 …(1) …(1) |
|
(解説)
(参考1)
列ベクトル , , ···, を束にした行列を
n次正方行列Aが相異なるn個の実数の固有値 λ1 , λ2 , …, λn およびこれに対応する固有ベクトル , , ···, をもつとき,
A=λ1
A=λ2
………
A=λn
が成り立つ.
P=[ , , ···, ]
で表すと,(参考1)の関係式は
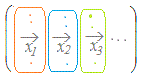
 |
|
すなわち
A[ , , ···, ]=[ λ1 , λ2 , ···, λn ]
と書ける.AP=[ λ1 , λ2 , ···, λn ]
(参考2)
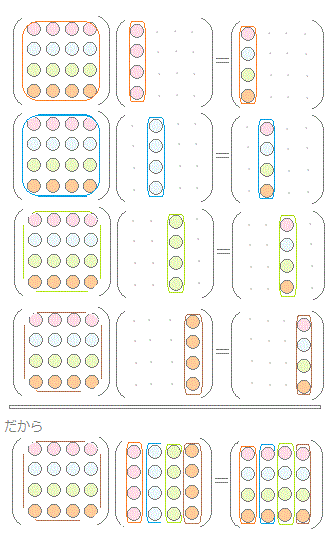
(a) (行列)×(列ベクトル)=(列ベクトル)になる 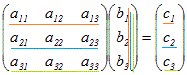 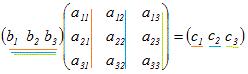 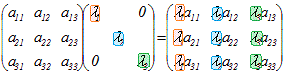 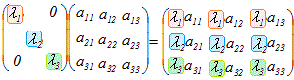 |
|
ここで,(参考2)の(c)を見ると,各列ベクトルごとに固有値λkを掛けるには,右から対角行列を掛ければよいから,この式は
AP=P
と表せる.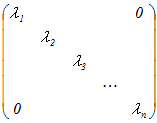 …(2) …(2)
|
|
したがって,もし行列Pに逆行列P−1が存在すれば(=行列Pが正則行列であれば),(2)の両辺に左からP−1を掛ければ(1)が得られる.
(参考3)
行列Pに逆行列P−1が存在することは,(参考3)によって分かる.
(e) 相異なる固有値に対応する固有ベクトルは1次独立である. (f) n次正方行列Pのn個の列ベクトルが1次独立であるならば,行列Pは正則すなわち逆行列が存在する. |
|
【要点2】
上の【要点1】によりn次正方行列Aが相異なるn個の実数の固有値をもつとき,Aを対角化するには次の手順で行えばよい.
(1) Aの固有値をn個求める.
(2) 各々の固有値に対応する固有ベクトルを求める. (3) 固有ベクトルを順に束ねた行列をP,固有値を順に対角成分とする行列をDとおく, (ただし,固有値,固有ベクトルは対応する順に並べる)
例1
(解答)次の行列を対角化せよ. 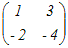 (1) 固有方程式を解いて固有値を求める.
det(A−λE)=
(2) 固有ベクトルを求める
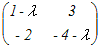 =0 =0⇔ (1−λ)(−4−λ)+6=0 ⇔ λ2+3λ+2=0 ⇔ λ=−1, −2
1) λ=−1のとき
(3)
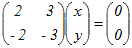 ⇔ 2x+3y=0 ⇔ 2x+3y=0⇔ (x, y)=t(3, −2) 2) λ=−2のとき 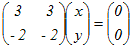 ⇔ x+y=0 ⇔ x+y=0⇔ (x, y)=t(1, −1)
P=
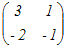 , P−1= , P−1=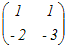 , D= , D=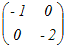 とおくと P−1AP= 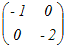
例2
(解答)次の行列を対角化せよ. 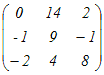 …(この解答は「各場面で求めているもののイメージをつかむため」の例示であり,実際に固有値,固有ベクトルなどを求めるにはExcelで行えばよい.)… (1) 固有方程式を解いて固有値を求める.
det(A−λE)=
(2) 固有ベクトルを求める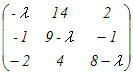 =0 =0⇔ λ3−17λ2+94λ−168=0 この3次方程式は筆算では「因数定理を使って解く」ことになるが,上に述べたように実際にはExcelで固有値を求めるとよい. ⇔ λ=4, 6, 7 1) λ=4のとき 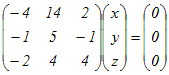
(*2), (*3)より
(*4)に代入 x+(y)=(5y) → x=(4y) ⇔ x=(4y), z=(y) → x=4t, y=t, z=t ⇔ (x, y, z)=t(4, 1, 1) 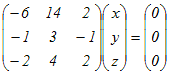
(*2), (*3)より
(*4)−(*5) 2z=(y) ⇔ x=5t, y=2t, z=t ⇔ (x, y, z)=t(5, 2, 1) 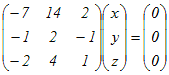
(*4)+(*5) x=(2y) これらを(*1)に代入すると成立するから(*1)は不要 ⇔ x=(2y), z=0 → x=2t, y=t, z=0 ⇔ (x, y, z)=t(2, 1, 0)
P=
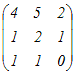 , P−1= , P−1=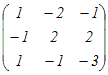 , ,D= 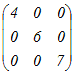 とおくと P−1AP= 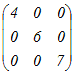
例3
(解答)次の行列を対角化せよ. (筆算では無理なのでExcelで求めるものとし,小数第4位まで求めよ.)
次の対角行列Dに対して
P−1AP=Dとなる. |
|
この項目では,wxMaxiam(インストール方法)を用いて固有値,固有ベクトルを求めて比較的簡単に行列を対角化する方法を解説する.
類題2.1
(解答)次の行列を対角化せよ. 出典:「線形代数学」掘内龍太郎.浦部治一郎共著(学術出版社)p.171
○1 行列Aの成分を入力するには
これらを束ねて書くと
メニューから「代数」→「手入力による行列の生成」と進み,入力欄において行数:3,列数:3,タイプ:一般,変数名:AとしてOKボタンをクリック
入力欄に与えられた成分を書き込む.(タブキーを使って入力欄を移動するとよい)
A: matrix(
[0,1,-2], [-3,7,-3], [3,-5,5] ); のように出力され,行列Aに上記の成分が代入されていることが分かる. ○2 Aの固有値と固有ベクトルを求めるには
wxMaximaで,固有値を求めるコマンドは eigenvalus(A),固有ベクトルを求めるコマンドは eigenvectors(A)であるが,固有ベクトルを求めると各固有値,各々の重複度,固有ベクトルの順に表示されるので,直接に固有ベクトルを求めるとよい.
画面上で空打ちして入力欄を作り, eigenvectors(A)+Shift+Enterとする.または,上記の入力欄のAをポイントしてしながらメニューから「代数」→「固有ベクトル」と進む [[[1,2,9],[1,1,1]],[[[1,1/3,-1/3]],[[1,0,-1]],[[1,3,-3]]]] のように出力される. これは 固有値λ1=1の重複度は1で,対応する固有ベクトルは 固有値λ2=2の重複度は1で,対応する固有ベクトルは 固有値λ3=9の重複度は1で,対応する固有ベクトルは となることを示している. ○3 固有値と固有ベクトルを使って対角化するには 上記の結果を行列で表すと 両辺に左から ※結果のまとめ 固有ベクトル 固有値を対角成分に持つ行列を とおくと となる.対角行列のn乗は各成分のn乗になるから,(1)を利用すれば,行列Aのn乗は簡単に求めることができる.(※) もしくは,(1)を変形しておいて これより さらに を用いると,Anを成分に直すこともできるがかなり複雑になる.
(※)
(1)式のように,ある行列Pとその逆行列P−1でサンドイッチになっている行列P−1APのn乗を計算すると,先頭と末尾が次々にEとなって消える: 2乗:(P−1AP)(P−1AP)=PAPP−1AP=PA2P−1 3乗:(P−1A2P)(P−1AP)=PA2PP−1AP=PA3P−1 4乗:(P−1A3P)(P−1AP)=PA3PP−1AP=PA4P−1 対角行列のn乗は,各成分をn乗すれば求められる:
(※)
生成AIで求めるにはwxMaximaを用いて(1)式などを検算するには,1-1で行ったように行列Aを定義し,さらにP,Dもその成分の値を入れて定義すると
行列の積APは A.P によって計算できる
実際に計算してみると,(行列の積はアスタリスク(*)ではなくドット(.)を使うことに注意.*を使うと各成分を単純に掛けたものになる) のように一致することが確かめられる. また,wxMaximaにおいては,Pの逆行列を求めるコマンドは P^(-1) などではなく,invert(P)であることに注意すると(1)式は invert(P).A.P; で計算することになり,これが対角行列と一致する. Google Gemini,ChatGPT,Microsoft Copilot, YAHOO! 検索(AIアシスタント)などの生成AIを使って,上記の問題を解くには
次の行列を対角化せよ. A=\begin{pmatrix}0 & 1 & -2 \\ -3 & 7 & -3 \\ 3 & -5 & 5 \end{pmatrix}
と,直接記入すれば途中経過と解答が得られる.ただし,「対角化とは何か?」というレベルの人は,もっと前の定義から読むべきでしょう.(以下の問題も同様)※いつも,複数ルートで点検できるようにしておくのは,よいことです. |
|
類題2.2
(解答)次の行列を対角化し,Bnを求めよ. 出典:「線形代数学」掘内龍太郎.浦部治一郎共著(学術出版社)p.171
○1 行列Bの成分を入力するには
これらを束ねて書くと
メニューから「代数」→「手入力による行列の生成」と進み,入力欄において行数:3,列数:3,タイプ:一般,変数名:BとしてOKボタンをクリック
入力欄に与えられた成分を書き込む.(タブキーを使って入力欄を移動するとよい)
B: matrix(
[6,6,6], [-2,0,-1], [2,2,3] ); のように出力され,行列Bに上記の成分が代入されていることが分かる. ○2 Bの固有値と固有ベクトルを求めるには
画面上で空打ちして入力欄を作り, eigenvectors(B)+Shift+Enterとする.または,上記の入力欄のBをポイントしてしながらメニューから「代数」→「固有ベクトル」と進む [[[1,2,6],[1,1,1]],[[[0,1,-1]],[[1,-4/3,2/3]],[[1,-2/5,2/5]]]] のように出力される. これは 固有値λ1=1の重複度は1で,対応する固有ベクトルは 固有値λ2=2の重複度は1で,対応する固有ベクトルは 固有値λ3=6の重複度は1で,対応する固有ベクトルは となることを示している. ○3 固有値と固有ベクトルを使って対角化するには 上記の結果を行列で表すと 両辺に左から ※結果のまとめ 固有値を対角成分に持つ行列を とおくと となる. ○4 Bnを求める. さらに を用いると,Bnを成分に直すこともできるがかなり複雑になる. |
|
問題
次の行列を対角化せよ. (筆算では無理なのでExcelで求めるものとし,小数第3位まで求めよ.Web画面をドラッグ・コピーしてからExcel上に貼り付けると入力の手間が省ける.)
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(解答)
次の対角行列Dに対して
P−1AP=Dとなる. |