|
← PC用は別頁
■ 共通部分,和集合
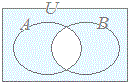
(1) 2つの集合A , Bの両方に属する要素全体の集合をA , Bの共通部分といいA∩Bで表す.
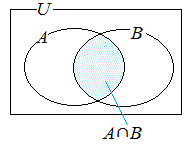 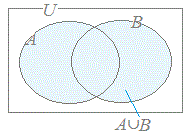
(1) 共通部分は集合の要素が満たすべき条件を「かつ」で結んだ場合に対応している.
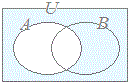
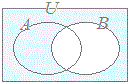
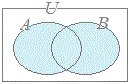
※ 数学で使われる「AまたはB( A or B )」という用語は,上の(2)から分かるようにAだけ,Bだけというようなどちらか一方だけの場合だけでなく,A∩Bの場合も含んでいることに注意 したがって,Aが朝にコーヒーを飲む人の集合,Bを朝に紅茶を飲む人の集合とするとき,A∪Bには両方とも飲む人も含まれている. 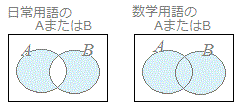 A = { 1 , 2 } , B = { 2 , 3 }のときA∩Bを要素を書き並べて示しなさい. (解答) A∩B = { 2 } 例2 A = { 1 , 2 } , B = { 2 , 3 }のときA∪Bを要素を書き並べて示しなさい. (解答) A∪B = { 1 , 2 , 3 } 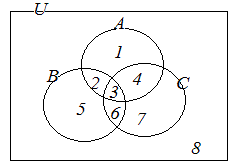 例3 例3右図において(A∩C)∪Bを要素を書き並べて示しなさい. (解答) A∩C = { 4 , 3 } B = { 2 , 3 , 5 , 6 } だから (A∩C)∪B = { 2 , 3, 4 , 5 , 6 } |
|
共通部分や和集合が組み合わされているときは,かっこの中を先に考えて合成する. (1) (A∩B)∪Cを図示するには 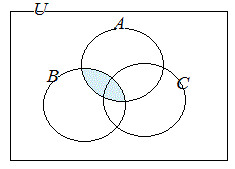 ∪ ∪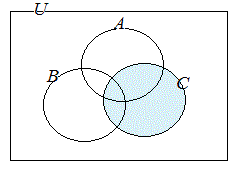 次に,それらの和集合を考える. ⇒ 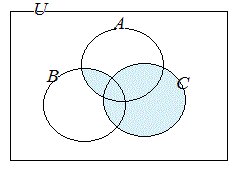 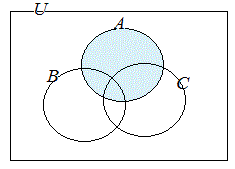 ∩ ∩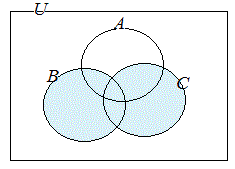 次に,それらの共通部分を考える. ⇒ 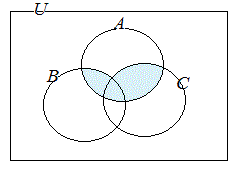
一般に(A∩B)∪CとA∩(B∪C)は異なる集合になるので,式の中に使われている「かっこ」は省略できない. これに対して,(A∩B)∩CとA∩(B∩C)は常に同じ集合になり,どちらの意味に理解されても混乱は起こらないのでA∩B∩Cと書くことができる. 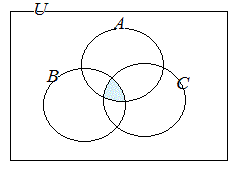 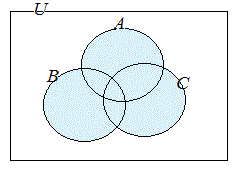 |
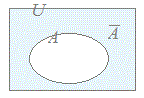
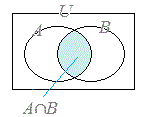 ⇒
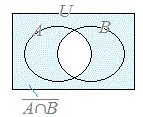
⇒ 
 ∩
∩
 ”屋根”がつながっているかどうかで全く違うものになる(←
”屋根”がつながっているかどうかで全く違うものになる(←
 …(i)
…(i)
 …(i)
…(i)