← PC用は別頁

== 部分集合，集合の包含関係 ==

【 要点 】
■　部分集合を表わす記号 A⊂B

○ 　次図アのように，集合 A のどの要素も集合 B の要素になっているとき（x∈A ならば x∈B のとき ）， A は B の部分集合であるといい，A⊂B で表わす．
※　∈ の記号は 要素と集合の関係に使い，
⊂ の記号は集合と集合の関係に使う．
○ 　次図イのときは，B⊂A となる．
※ B⊃A は A⊂B と同じ，A⊃B は B⊂A と同じ．
（小さい方）⊂（大きい方）　の形になっていればよい．
■　集合が等しいことを表わす記号 A=B

○ 　次図ウのように，２つの集合 A , B の要素が完全に一致するとき，A=B と書く．
例　A={ 1 , 2 , 3} ， B={ 1 , 2 , 3} のとき A=B

A⊂B の記号について，下の注意書参照

○　A⊂B のときに B の要素のうち A の要素でないものが実際にあるとき，A は B の真部分集合であるという．
例　A={ 1 , 2} は B={ 1 , 2 , 3} の真部分集合

○　数の大小関係では 3<x かつ x<3 などということはないが，x≦3 かつ 3≦x のとき x=3 になるのと同様に，集合では B⊂A かつ A⊂B のとき A=B が成り立つ．

○ 　B⊂A かつ A⊂B が言えれば，A=B としてよい

　集合 A , B の要素が簡単に比較できないときにも，B⊂A かつ A⊂B が言えれば，A=B としてよい．

■　集合の包含関係とは

○　次図アイウのように A⊂B，B⊂A，A=B のいずれかの関係が成り立つとき，２つの集合 A , B には包含関係があるという．

　これに対して，次図エオのように上記いずれの関係も成り立たないとき，２つの集合 A , B には包含関係がないという．
　包含関係がないときには， A だけ B だけに入るものがそれぞれ存在する．
　
例　A が犬の集合，B が猫の集合とすると，図オのようになって包含関係はない．
例　A={ 1 , 2 , 3 } , B={ 1 , 2 , 4 } のとき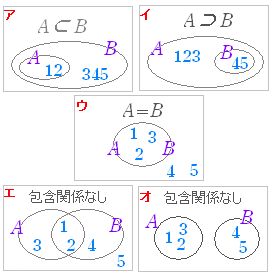
3∈A かつ 3|∈B，　4∈B かつ 4A
だから，A , B には包含関係はない．


※ （注意）
　今の高校数学では，A が B の真部分集合の場合と，A=B の場合を含めて，部分集合を A⊂B という記号で表わす．
（もし不等号を連想するのであれば＜ではなく，≦に対応するので要注意･･･昔は似ていたが今は似ていないということ）
　かなり前の高校での記号
真部分集合
（部分集合だが等しくはない）		A⊂BA は B の
部分集合
AB
等しいA=B

　今の高校での記号
真部分集合
（部分集合だが等しくはない）		A⊂B かつ A≠B
（ AB ）
A は B の
部分集合

A⊂B
等しいA=B

　参考：不等号の記号
小さい
（等しく場合を含まない）		x<3
x≦3
等しいx=3

問題__________[ 第1面 / 全2面中 ] 　次の集合 A , B の包含関係を調べ，記号で答えよ．（初めに問題文中のを選び，続いて下の選択肢を選べ．包含関係がないときはを選べ．合っていればその記号に変る．）

［選択肢］　　__________________

...（携帯版）メニューに戻る

...メニューに戻る

■［個別の頁からの質問に対する回答］[部分集合，集合の包含関係について／17.2.18］
問題についての質問です (2)　A={2n | 0≦n≦5 , n は整数} , B={n | n は32の約数} のとき， A ？ B という問題で答えは＝となっていますが、32の約数には1も含まれると思うので正答は なし ではないのですか？ それと、部分集合と真部分集合の違いがよく分からないので詳しく説明して欲しいです。 よろしくお願いします。
＝＞［作者］：連絡ありがとう．「32の約数には1も含まれる」のでA=Bなのです．
「AがBの部分集合：A⊂Bであって，かつ，A≠B」のとき，したがって「A⊂Bであって，かつ，Bの中にAでないものが実際に存在するとき」AはBの真部分集合になります．このことは，※ （注意）のところに書いています．
ところで，あなたが分からないのは部分集合と真部分集合の関係ではなく指数関数，特に20だと考えられます．この頁（数学Ⅱの内容）に解説していますが，20=1です．したがって，A={2n | 0≦n≦5 , nは整数}のとき，A={1,2,4,8,16,32}になります．