三角関数の加法定理、倍角公式、３倍角公式、半角公式

大きな区分

現在地と前後の項目

正の角・負の角/動径の表わす一般角/三角関数の定義 /(第2象限) /(第3象限) /(第4象限) /(まとめ)/弧度法の単位：ラジアン/三角関数の値(よく使う角度)/sin(π+θ)など/三角方程式　/三角不等式/三角関数のグラフ(sinθの平行移動)/(cosθの平行移動)/sin(θ－α)のグラフ（解説）/(振幅)/(周期)/(周期と振幅)/三角関数のグラフ(総合1)/三角関数のグラフ(総合2)/加法定理，倍角公式，３倍角公式，半角公式/加法定理の練習問題/２倍角公式.半角公式/加法定理の数値計算/積和.和積の公式/練習問題2/練習問題3/練習問題4/合成公式/三角不等式/三角関数（まとめ）/[センター]積和の公式/[センター]合成公式/三角関数公式一覧/三角関数公式プラス/三角形の証明・形状問題/センター試験.三角関数(2015年～)/

=== 【三角関数の加法定理など公式一覧】 ===

(*)で示したものは，通常は覚えない．
必要になってから作るくらいの構えでよい．

[1]　加法定理

\sin (α + β) = \sin α \cos β + \cos α \sin β

…(1.1)

\sin (α - β) = \sin α \cos β - \cos α \sin β

…(1.2)

\cos (α + β) = \cos α \cos β - \sin α \sin β

…(1.3)

\cos (α - β) = \cos α \cos β + \sin α \sin β

…(1.4)

\tan (α + β) = \frac{\tan α + \tan β}{1 - \tan α \tan β}

…(1.5)

\tan (α - β) = \frac{\tan α - \tan β}{1 + \tan α \tan β}

…(1.6)

\cot (α + β)

= \frac{1}{\tan (α + β)} = \frac{1 - \tan α \tan β}{\tan α + \tan β}

= \frac{\frac{1}{\tan α \tan β} - 1}{\frac{1}{\tan β} + \frac{1}{\tan α}}

= \frac{\cot β \cot α - 1}{\cot β + \cot α}

…(*1.7)

\cot (α - β)

= \frac{1}{\tan (α - β)} = \frac{1 + \tan α \tan β}{\tan α - \tan β}

= \frac{\frac{1}{\tan α \tan β} + 1}{\frac{1}{\tan β} - \frac{1}{\tan α}}

= \frac{\cot β \cot α + 1}{\cot β - \cot α}

…(*1.8)

\sin (α + β + γ)

= \sin (α + β) \cos γ + \cos (α + β) \sin γ

= (\sin α \cos β + \cos α \sin β) \cos γ

+ (\cos α \cos β - \sin α \sin β) \sin γ

…(*1.9)

\cos (α + β + γ)

= \cos (α + β) \cos γ - \sin (α + β) \sin γ

= (\cos α \cos β - \sin α \sin β) \cos γ

- (\sin α \cos β + \cos α \sin β) \sin γ

…(*1.10)

[2]　２倍角公式

\sin 2 α = 2 \sin α \cos α

…(2.1)

← (1.1)より

\sin (α + α) = \sin α \cos α + \cos α \sin α

だから成り立つ

\cos 2 α = \cos^{2} α - \sin^{2} α

…(2.2)

← (1.3)より

\cos (α + α) = \cos α \cos α - \sin α \sin α

だから成り立つ

= 2 \cos^{2} α - 1

…(2.3)

← (2.2)より

\cos^{2} α - \sin^{2} α = \cos^{2} α - (1 - \cos^{2} α)

= 2 \cos^{2} α - 1

だから成り立つ

= 1 - 2 \sin^{2} α

…(2.4)

← (2.2)より

\cos^{2} α - \sin^{2} α = (1 - \sin^{2} α) - \sin^{2} α

= 1 - 2 \sin^{2} α

だから成り立つ

\tan 2 α = \frac{2 \tan α}{1 - \tan^{2} α}

…(2.5)

← (1.5)より

\tan (α + α) = \frac{\tan α + \tan α}{1 - \tan α \tan α}

= \frac{2 \tan α}{1 - \tan^{2} α}

だから成り立つ

\cot 2 α = \frac{\cot^{2} α - 1}{2 \cot α}

…(*2.6)

← (*1.7)より

\cot (α + α) = \frac{\cot α \cot α - 1}{\cot α + \cot α}

= \frac{\cot^{2} α - 1}{2 \cot α}

だから成り立つ

※

\cot x

について，質問が多いので，メモ書き
　

\cot x

（コタンジェントエックス）は

\cos x

（コサインエックス）の入力ミスではありません．

c o t x, s e c x, c o s e c x

は，今日の高校数学では習わない場合がありますが，理系の大学では「当然分かっているもの」として扱われますので，注意してください．

c o s e c x = \frac{1}{\sin x}

s e c x = \frac{1}{\cos x}

c o t x = \frac{1}{\tan x}

　要するに，３文字目に赤で示した三角関数

s i n x, c o s x, t a n x

の逆数と覚えるとよい．
※ただし，英語圏では，

c o s e c x

の代わりに，

\csc x

と書かれることが多い=３文字がお好き？

[3]　半角公式

※半角公式は

\cos 2 α

に関する２倍角公式(2.3)(2.4)と同じものと考えればよい．

\sin^{2} α = \frac{1 - \cos 2 α}{2}

…(3.1.1)

← (2.4)より

\cos 2 α = 1 - 2 \sin^{2} α

だから

\sin^{2} α = \frac{1 - \cos 2 α}{2}

が成り立つ

この半角公式は，次の形で書かれることもある．この場合，符号は角度

α

の象限に応じてどちらか一方を選ぶことになる．

\sin α = \pm \sqrt{\frac{1 - \cos 2 α}{2}}

…(3.1.2)
この半角公式は，次の形で書かれることもある．この場合，倍角を

α

と書いていることになる．

\sin^{2} \frac{α}{2} = \frac{1 - \cos α}{2}

…(3.1.3)

\sin \frac{α}{2} = \pm \sqrt{\frac{1 - \cos α}{2}}

…(3.1.4)

※数学なんて冷たい論理の世界の話で，好き嫌いのような個人的な感情を持ち込むのは場違いのように見えますが，いざ使おうとなると各自の内的な思考を再現することになります．
そこで，(3.1.1)～(3.1.4)まで全部覚えようとするのは不利なので，どれか１つ確実にいえるものを覚えるとよい．
筆者は(3.1.1)が好みである．シンプルでかつ符号がコテコテしていないから．

\cos^{2} α = \frac{1 + \cos 2 α}{2}

…(3.2.1)

← (2.3)より

\cos 2 α = 2 \cos^{2} α - 1

だから

\cos^{2} α = \frac{1 + \cos 2 α}{2}

が成り立つ

この半角公式は次の形で書かれることもある．

\cos α = \pm \sqrt{\frac{1 + \cos 2 α}{2}}

…(3.2.2)

\cos^{2} \frac{α}{2} = \frac{1 + \cos α}{2}

…(3.2.3)

\cos \frac{α}{2} = \pm \sqrt{\frac{1 + \cos α}{2}}

…(3.2.4)

※上記と同様にして，筆者の好みは(3.2.1)である．

\tan^{2} α = \frac{1 - \cos 2 α}{1 + \cos 2 α}

…(3.3.1)

← (3.1.1)(3.2.1)より

\tan^{2} α = \frac{\sin^{2} α}{\cos^{2} α} = \frac{1 - \cos 2 α}{1 + \cos 2 α}

だから成り立つ

この半角公式は次の形で書かれることがある．

\tan α = \pm \sqrt{\frac{1 - \cos 2 α}{1 + \cos 2 α}}

…(3.3.2)

\tan^{2} \frac{α}{2} = \frac{1 - \cos α}{1 + \cos α}

…(3.3.3)

\tan \frac{α}{2} = \pm \sqrt{\frac{1 - \cos α}{1 + \cos α}}

…(3.3.4)

(3.3.2)(3.3.4)のように

\pm \sqrt{\frac{\dots}{\dots}}

の形で書かれる公式では，角度が属する象限に応じていずれか1つの符号を選ばなければならないが，次の形ではその心配はない．

\tan α = \frac{\sin 2 α}{1 + \cos 2 α}

…(*3.3.5)

←

\tan α = \frac{\sin α}{\cos α} = \frac{\sin α \cos α}{\cos^{2} α}

= \frac{2 \sin α \cos α}{2 \cos^{2} α} = \frac{\sin 2 α}{1 + \cos 2 α}

だから成り立つ

\tan \frac{α}{2} = \frac{\sin α}{1 + \cos α}

…(*3.3.6)

※

1 + \cos α > 0

だから，この関係式は

\tan \frac{α}{2}

の符号と

\sin α

の符号がつねに等しいことを表している．

\tan α = \frac{1 - \cos 2 α}{\sin 2 α}

…(*3.3.7)

\tan \frac{α}{2} = \frac{1 - \cos α}{\sin α}

…(*3.3.8)

※

1 - \cos α ≧ 0

だから，この関係式は

\tan \frac{α}{2}

の符号と

\sin α

の符号がつねに等しいことを表している．

[4]　

\tan \frac{α}{2} = t

を用いて三角関数を有理関数（分数関数）に書き換える方法

\tan \frac{α}{2} = t

とおくと

\tan α = \frac{2 t}{1 - t^{2}}

…(4.1)

←(2.5)より

\tan α = \frac{2 \tan \frac{α}{2}}{1 - \tan^{2} \frac{α}{2}} = \frac{2 t}{1 - t^{2}}

だから成り立つ

\sin α = \frac{2 t}{1 + t^{2}}

…(4.2)

←

\sin α = 2 \sin \frac{α}{2} \cos \frac{α}{2}

= 2 \frac{\sin \frac{α}{2}}{\cos \frac{α}{2}} \cos^{2} \frac{α}{2} = 2 \tan \frac{α}{2} \frac{1}{1 + \tan^{2} \frac{α}{2}}

= \frac{2 t}{1 + t^{2}}

だから成り立つ

\cos α = \frac{1 - t^{2}}{1 + t^{2}}

…(4.3)

←(4.2)÷(4.1)

※(4.2)(4.3)は分母が共通で，分子の比が(4.1)になります

[5]　3倍角公式，４倍角，･･･

\sin 3 α = 3 \sin α - 4 \sin^{3} α

…(5.1)

← (1.1)より

\sin (2 α + α) = \sin 2 α \cos α + \cos 2 α \sin α

= 2 \sin α \cos α \cdot \cos α + (1 - 2 \sin^{2} α) \sin α

= 2 \sin α \cos^{2} α + (1 - 2 \sin^{2} α) \sin α

= 2 \sin α (1 - \sin^{2} α) + (1 - 2 \sin^{2} α) \sin α

= 3 \sin α - 4 \sin^{3} α

だから成り立つ
※sin3αはsinαで表せる．

\cos 3 α = - 3 \cos α + 4 \cos^{3} α

…(5.2)

← (1.3)より

\cos (2 α + α) = \cos 2 α \cos α - \sin 2 α \sin α

= (2 \cos^{2} α - 1) \cos α - (2 \sin α \cos α) \sin α

= (2 \cos^{2} α - 1) \cos α - 2 \sin^{2} α \cos α

= (2 \cos^{2} α - 1) \cos α - 2 (1 - \cos^{2} α) \cos α

= - 3 \cos α + 4 \cos^{3} α

だから成り立つ
※cos3αはcosαで表せる．
cosにしたら符号が変わる．

※「sinnαはsinαで表せる．cosnαはcosαで表せそうだ．」というのは，当てはまる場合と当てはまらない場合があります．

\sin 2 α = 2 \sin α \cos α

←cosα含み

\sin 3 α = 3 \sin α - 4 \sin^{3} α

←sinαだけで表せる

\sin 4 α = 4 \sin α \cos α - 8 \sin^{3} α \cos α

←cosα含み

\sin 5 α = 5 \sin α - 20 \sin^{3} α + 16 \sin^{5} α

←sinαだけで表せる

\cos 2 α = - 1 + 2 \cos^{2} α

←cosαだけで表せる

\cos 3 α = - 3 \cos α + 4 \cos^{3} α

←cosαだけで表せる

\cos 4 α = 1 - 8 \cos^{2} α + 8 \cos^{4} α

←cosαだけで表せる

\cos 5 α = 5 \cos α - 20 \cos^{3} α + 16 \cos^{5} α

←cosαだけで表せる

[6]　積を和に直す公式

\sin α \cos β = \frac{1}{2} {\sin (α + β) + \sin (α - β)}

…(6.1)

\cos α \sin β = \frac{1}{2} {\sin (α + β) - \sin (α - β)}

…(6.2)

\cos α \cos β = \frac{1}{2} {\cos (α + β) + \cos (α - β)}

…(6.3)

\sin α \sin β = - \frac{1}{2} {\cos (α + β) - \cos (α - β)}

…(6.4)

加法定理(1.1)～(1.4)を用いて，各式の右辺を展開してみると証明できる．

[7]　和を積に直す公式

\sin A + \sin B = 2 \sin \frac{A + B}{2} \cos \frac{A - B}{2}

…(7.1)

\sin A - \sin B = 2 \cos \frac{A + B}{2} \sin \frac{A - B}{2}

…(7.2)

\cos A + \cos B = 2 \cos \frac{A + B}{2} \cos \frac{A - B}{2}

…(7.3)

\cos A - \cos B = - 2 \sin \frac{A + B}{2} \sin \frac{A - B}{2}

…(7.4)

(6.1)～(6.4)において

A = α + β, B = α - β

とおくと

α = \frac{A + B}{2}, β = \frac{A - B}{2}

となる．左辺と右辺を入れ換えると(7.1)～(7.2)になる．

[8]　三角数列の和

\sin x + \sin 2 x + \dots + \sin n x

= \frac{\sin \frac{n + 1}{2} x \sin \frac{n}{2} x}{\sin \frac{x}{2}}

…(*8.1)

\cos x + \cos 2 x + \dots + \cos n x

= \frac{\cos \frac{n + 1}{2} x \sin \frac{n}{2} x}{\sin \frac{x}{2}}

…(*8.2)

（解説）
積を和に直す公式(6.4)

\sin α \sin β = - \frac{1}{2} {\cos (α + β) - \cos (α - β)}

をうまく使うと

\sin x \sin \frac{x}{2} = - \frac{1}{2} {\underset{―}{\cos \frac{3}{2} x} - \cos \frac{1}{2} x}

\sin 2 x \sin \frac{x}{2} = - \frac{1}{2} {\cos \frac{5}{2} x - \underset{―}{\cos \frac{3}{2} x}}

のように，各項を引き算に分けることができる．このとき，前の項でプラスになるものと後の項でマイナスのなるものがちょうど打ち消しあうように，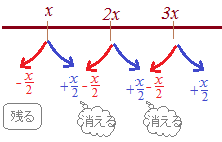

\times \sin \frac{x}{2}

の形を作っていくところがミソ．

元の問題が

\sin x + \sin 2 x + \dots + \sin n x

であるのに，「勝手に」

\sin \frac{x}{2}

を掛けて

(\sin x + \sin 2 x + \dots + \sin n x) \sin \frac{x}{2}

を計算する．うまく答が出たら，結果を

\sin \frac{x}{2}

で割るのである．（掛けて割ったら元へと戻る）

\sin x \sin \frac{x}{2} = - \frac{1}{2} {\cos \frac{3}{2} x - \cos \frac{1}{2} x}

\sin 2 x \sin \frac{x}{2} = - \frac{1}{2} {\cos \frac{5}{2} x - \cos \frac{3}{2} x}

\sin 3 x \sin \frac{x}{2} = - \frac{1}{2} {\cos \frac{7}{2} x - \cos \frac{5}{2} x}

\dots \dots \dots \dots \dots \dots

\underset{―}{+) \sin n x \sin \frac{x}{2} = - \frac{1}{2} {\cos \frac{2 n + 1}{2} x - \cos \frac{2 n - 1}{2} x}}

辺々加えると，右辺の中間項が消えて，先頭と末尾だけが残る．

(\sin x + \sin 2 x + \dots + \sin n x) \sin \frac{x}{2}

= - \frac{1}{2} {\cos \frac{2 n + 1}{2} x - \cos \frac{1}{2} x}

…(*)

次に，和を積に直す公式(7.4)

\cos A - \cos B = - 2 \sin \frac{A + B}{2} \sin \frac{A - B}{2}

において

A = \frac{2 n + 1}{2} x, B = \frac{1}{2} x

とおくと

\frac{A + B}{2} = \frac{n + 1}{2} x, \frac{A - B}{2} = \frac{n}{2} x

だから，(*)の右辺は

= - \frac{1}{2} \times (- 2) \sin \frac{n + 1}{2} x \sin \frac{n}{2} x = \sin \frac{n + 1}{2} x \sin \frac{n}{2} x

したがって

(\sin x + \sin 2 x + \dots + \sin n x) \sin \frac{x}{2} = \sin \frac{n + 1}{2} x \sin \frac{n}{2} x

両辺を

\sin \frac{x}{2}

で割ると，求めるべき和が得られる．

\sin x + \sin 2 x + \dots + \sin n x = \frac{\sin \frac{n + 1}{2} x \sin \frac{n}{2} x}{\sin \frac{x}{2}}

※同様にして(6.2)を使って(8.2)を示すことができます．

※(6.1)を利用して

\cos \frac{x}{2}

を掛けてから割るという方法でもできます．

※複素数についてのド・モアブルの定理を習っている場合には，次のように「等比数列の和」で求めることもできる．
【ド・モアブルの定理】

(\cos θ + i \sin θ)^{n} = \cos n θ + i \sin n θ

により

(\cos x + i \sin x) + (\cos x + i \sin x)^{2} + \dots + (\cos x + i \sin x)^{n}

= \cos x + \cos 2 x + \dots + \cos n x

+ i (\sin x + \sin 2 x + \dots + \sin n x)

の虚部を求めたらよい．

(\cos x + i \sin x) + (\cos x + i \sin x)^{2} + \dots + (\cos x + i \sin x)^{n}

は，初項

(\cos x + i \sin x)

，公比

(\cos x + i \sin x)

，項数nの等比数列の和だから

\frac{(\cos x + i \sin x) {1 - (\cos x + i \sin x)^{n}}}{1 - (\cos x + i \sin x)}

= \frac{(\cos x + i \sin x) {1 - (\cos n x + i \sin n x)}}{1 - (\cos x + i \sin x)}

以上のように理屈は簡単であるが，この後で実部と虚部を分けて虚部を取り出す計算は結構長くなる．
この計算を簡単にする工夫として，分母が共役複素数の差となるように，分母分子に

\cos (- \frac{x}{2}) + i \sin (- \frac{x}{2})

を掛ける．

分母では，

1 (\cos (- \frac{x}{2}) + i \sin (- \frac{x}{2})) = \cos (- \frac{x}{2}) + i \sin (- \frac{x}{2})

(\cos x + i \sin x) (\cos (- \frac{x}{2}) + i \sin (- \frac{x}{2}))

= \cos (\frac{x}{2}) + i \sin (\frac{x}{2})

など変形する

= \frac{(\cos \frac{x}{2} + i \sin \frac{x}{2}) {1 - (\cos n x + i \sin n x)}}{(\cos (- \frac{x}{2}) + i \sin (- \frac{x}{2})) - (\cos \frac{x}{2} + i \sin \frac{x}{2})}

= \frac{(\cos \frac{x}{2} + i \sin \frac{x}{2}) {1 - (\cos n x + i \sin n x)}}{- 2 i \sin \frac{x}{2}}

分母と分子にiを掛ける．分母では，−i×1=1になる

= \frac{(\cos \frac{x}{2} + i \sin \frac{x}{2}) {1 - (\cos n x + i \sin n x)} i}{2 \sin \frac{x}{2}}

この式の分子を展開するとできる．

= \frac{{(\cos \frac{x}{2} + i \sin \frac{x}{2}) - (\cos \frac{n + 1}{2} x + i \sin \frac{n + 1}{2} x)} i}{2 \sin \frac{x}{2}}

= \frac{(i \cos \frac{x}{2} - \sin \frac{x}{2}) - (i \cos \frac{n + 1}{2} x - \sin \frac{n + 1}{2} x)}{2 \sin \frac{x}{2}}

= \frac{\sin \frac{n + 1}{2} x - \sin \frac{x}{2} + i (\cos \frac{x}{2} - \cos \frac{n + 1}{2} x)}{2 \sin \frac{x}{2}}

したがって，虚部は

\frac{\cos \frac{x}{2} - \cos \frac{n + 1}{2} x}{2 \sin \frac{x}{2}}

実部は

\frac{\sin \frac{n + 1}{2} x - \sin \frac{x}{2}}{2 \sin \frac{x}{2}}

→(8.1)(8.2)

[9]　三角形の内角について成り立つ式
△ABCの内角A, B, Cについては次の等式が成り立つ．

\sin A + \sin B + \sin C = 4 \cos \frac{A}{2} \cos \frac{B}{2} \cos \frac{C}{2}

…(*9.1)

\cos A + \cos B + \cos C = 4 \sin \frac{A}{2} \sin \frac{B}{2} \sin \frac{C}{2} + 1

…(*9.2)

\tan A + \tan B + \tan C = \tan A \tan B \tan C

…(*9.3)

\cot A \cot B + \cot B \cot C + \cot C \cot A = 1

…(*9.4)

（解説）
△ABCの内角A, B, Cについては
A+B+C=π
が成り立つから
A+B=π−C

\sin (A + B) = \sin (π - C) = \sin C

また

\frac{A + B}{2} = \frac{π}{2} - \frac{C}{2}

\sin \frac{A + B}{2} = \sin (\frac{π}{2} - \frac{C}{2}) = \cos \frac{C}{2}

\cos \frac{A + B}{2} = \cos (\frac{π}{2} - \frac{C}{2}) = \sin \frac{C}{2}

などが成り立つ．これにより

←(*9.1)は次のように示せる．

\sin A + \sin B + \sin C = 2 \sin \frac{A + B}{2} \cos \frac{A - B}{2} + \sin C

= 2 \cos \frac{C}{2} \cos \frac{A - B}{2} + 2 \sin \frac{C}{2} \cos \frac{C}{2}

= 2 \cos \frac{C}{2} (\cos \frac{A - B}{2} + \sin \frac{C}{2})

= 2 \cos \frac{C}{2} (\cos \frac{A - B}{2} + \cos \frac{A + B}{2})

= 4 \cos \frac{C}{2} \cos \frac{A}{2} \cos \frac{B}{2}

←(*9.2)は次のように示せる．

\cos A + \cos B + \cos C = 2 \cos \frac{A + B}{2} \cos \frac{A - B}{2} + \cos C

= 2 \sin \frac{C}{2} \cos \frac{A - B}{2} + 1 - 2 \sin^{2} \frac{C}{2}

= 2 \sin \frac{C}{2} (\cos \frac{A - B}{2} - \sin \frac{C}{2}) + 1

= 2 \sin \frac{C}{2} (\cos \frac{A - B}{2} - \cos \frac{A + B}{2}) + 1

= 2 \sin \frac{C}{2} (- 2 \sin \frac{A}{2} \sin \frac{- B}{2}) + 1

= 4 \sin \frac{C}{2} \sin \frac{A}{2} \sin \frac{B}{2} + 1

←(*9.3)は次のように示せる．

\tan (A + B) = \tan (π - C) = - \tan C

\frac{\tan A + \tan B}{1 - \tan A \tan B} = - \tan C

\tan A + \tan B = - \tan C (1 - \tan A \tan B)

\tan A + \tan B + \tan C = \tan A \tan B \tan C

←さらに，この両辺を

\tan A \tan B \tan C

で割ると(*9.4)が示せる．

\frac{1}{\tan B \tan C} + \frac{1}{\tan C \tan A} + \frac{1}{\tan A \tan B} = 1

\cot B \cot C + \cot C \cot A + \cot A \cot B = 1

...（PC版）メニューに戻る

△このページの先頭に戻る△【アンケート送信】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．

○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）

質問に対する回答の中学版はこの頁，高校版はこの頁にあります