|
■ 一般角の定義 ■ 解説 小学校以来,右図のように,角度は分度器を用いて測り,0°~360°までとしてきた. さらに進んだ数学を学ぶためには,負の角や360°よりも大きい角度まで角度の範囲を広げて考える.このように意味を広げて拡張した角度を一般角という. |
 |
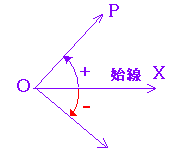
| 一般角は,x軸の正の向きOXを始線(0°)として,動径OP(動く半径という意味)を回転させて考え,「反時計回り」を正の向き,「時計回り」を負の向きと決める. 例 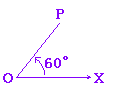 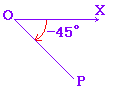 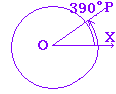 このように,一般角は動径を用いて表わす. |
 |
|
■ 一般角の定義 ■ 解説 小学校以来,右図のように,角度は分度器を用いて測り,0°~360°までとしてきた. さらに進んだ数学を学ぶためには,負の角や360°よりも大きい角度まで角度の範囲を広げて考える.このように意味を広げて拡張した角度を一般角という. |
 |
| 一般角は,x軸の正の向きOXを始線(0°)として,動径OP(動く半径という意味)を回転させて考え,「反時計回り」を正の向き,「時計回り」を負の向きと決める. 例 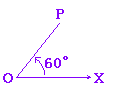   このように,一般角は動径を用いて表わす. |
 |
|
■[個別の頁からの質問に対する回答][一般角の定義について/18.7.21]
数学好きの僕にはたまらないwebだよ‼
本当にありがとう‼( ≧∀≦)ノ
■[個別の頁からの質問に対する回答][一般角の定義について/17.5.14]
=>[作者]:連絡ありがとう. いつも数学で分からないところが分かりやすく書かれていてとても助かっています。これからもよろしくお願いします(_ _)
■[個別の頁からの質問に対する回答][一般角の定義について/17.4.4]
=>[作者]:連絡ありがとう. いきなり、動径を動く半径と定義していますが、もともと動径は極座標を前提にしているものと思います。三角関数の表現のための「動径」であれば、単位円周上を動く点Pが点(1,0)を出発して回転するというイメージをはっきりさせてからのほうがわかりやすいのではないでしょうか。
=>[作者]:連絡ありがとう.あなたの考えは分かりましたが,極座標を習っていなくても動径は扱います.また単位円とは限りません. |
| ■このサイト内のGoogle検索■ |