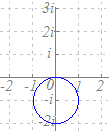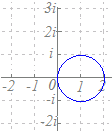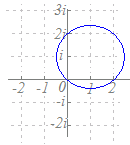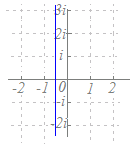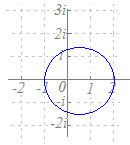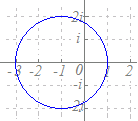|
【基本となる考え方】
2つの複素数z1 , z2間の距離は |z2−z1| ○ 定点からの距離が一定である点の軌跡
定点をA(α),動点をP(z),正の定数をrとするとき,
(解説)|z−α|=r (>0) を満たす点P(z)の軌跡はAを中心とする半径rの円になる. 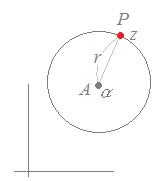
特に,|z|=rは原点を中心とする半径rの円になる.
図のように,定点A(α)から動点P(z)までの距離は|z−α|で,これが一定の値rになるのだから,円になります.
z=x+yi, α=a+biとして,|z−α|=rを(x, y)座標で表すと,
【例】=r (x−a)2+(y−b)2=r2 となって,数学IIで習う円の方程式と一致する. しかし,複素数で示された問題を常に(x, y)座標に直して考えていると能率が悪いので,特に行き詰ったときだけ(x, y)座標に直すようにし,複素数の問題は複素数のままで答えるようにするのがよい.
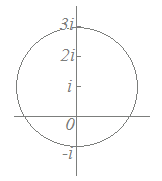
方程式|z−i|=2を満たす動点P(z)の軌跡は,iを中心とする半径2の円になる.
 ○ 2定点からの距離が等しい点の軌跡
2定点をA(α), B(β),動点をP(z)とするとき,
(解説)|z−α|=|z−β| を満たす点P(z)の軌跡は,線分ABの垂直二等分線になる. 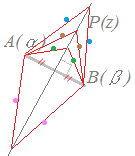 中学校で習うように,2定点からの距離が等しい点は垂直二等分線上にあります. 【例】
方程式|z−i|=|z+1|を満たす動点P(z)の軌跡は,2点i, −1を結ぶ線分の垂直二等分線になる.
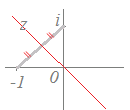
z=x+yiとおいて,以下のようにx, y座標で示すこともできるが,複素数の問題は複素数のまま答えるのがよく,元の問題の式を見て直接答えてよい.
|z−i|=|z+1|
→ |x+(y−1)i|=|(x+1)+yi| → = → x2+(y−1)2=(x+1)2+y2 → y=−x |
|
○ 2定点からの距離の比が一定(≠1)である点の軌跡
2定点をA(α), B(β),動点をP(z)とするとき,
【例】|z−α|:|z−β|=1:k ←→ |z−β|=k|z−α| を満たす点P(z)の軌跡は,アポロニウスの円になる.
アポロニウスは円,楕円,放物線などを研究したギリシャの数学者の名前.「アポロニウスの円」は,変な形ではなく,普通の円.「アポロニウスの・・・」というのは,「2定点からの距離の比が一定であるような点の軌跡」という,この円の作り方を表す言葉.
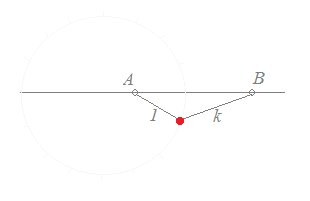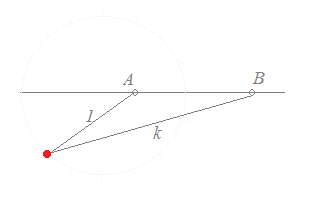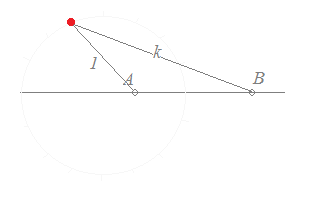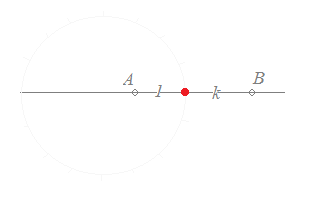 (1) AB間では,ABを1:kに内分する点を通る. (2) ABの外側では,(上の図は1<kの場合の例)ABを1:kに外分する点を通る. 以上により
|z−α|:|z−β|=1:k ←→ |z−β|=k|z−α|を満たす点P(z)の軌跡は,「A(α), B(β)を1:kに内分する点と1:kに外分する点を直径の両端とする円」になる.・・・長いセリフになるが,このように覚えるとよい.
円になることの証明は 1) xy座標に直す. 2) 中心と半径を用いて複素数の方程式直す. 3) 角の二等分線の性質を使って∠PABがつねに90°であることを示す. などによって行うことができるが,これらの変形は長くなるので,実際の問題を解くときは|z−β|=k|z−α|ときたら,アポロニウスの円になると覚えておく方がよい. 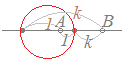
方程式2|z|=|z−3|を満たす動点P(z)の軌跡は,2点1, −3を直径の両端とする円になる.
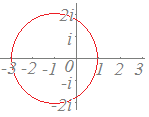
以下のように変形して示すこともできるが,長くなるので,「0と3を1:2に内分する点1」「0と3を1:2に外分する点−3」を直径の両端とする円と考える方がよい.
(参考)
4|z|2=|z−3|2
→ 4z=(z−3)( −3) → 4z=z−3z−3+9 → 3z+3z+3−9=0 → z+z+−3=0 → (z+1)( +1)=4 → |z+1|=2 ≪注意≫ 2定点からの距離の比が1:1 ⇒ 直線(半径が無限大の円) 2定点からの距離の比が1:k, k:1 (k≠1) ⇒ アポロニウスの円 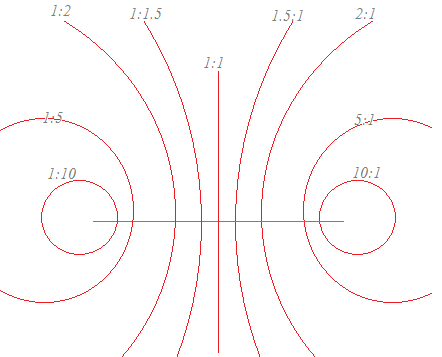 |
|
問題各々正しいものを選んでください.
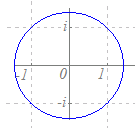
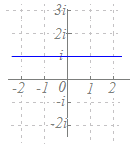
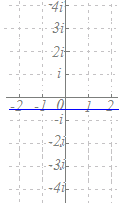
中心が原点0で,半径がの円だから,
|z|= なお,|z|=(const)の形ではなく,z=(const)の形になっている場合は,円ではなく1つの点を表すことに注意.
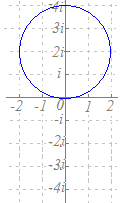
|z−(−i)|=1と変形すると,中心が−iで,半径が1の円を表すことがわかる.
中心が1+iで,半径がの円だから,
|z−1−i|=
2点1, −2を結ぶ線分の垂直二等分線になるので,
y軸に平行な直線x=−になります. |
|
式から見ると
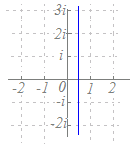
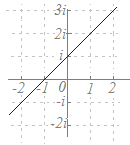
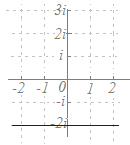
1) |z+1|=|z+1−2i|は−1, −1+2iを結ぶ線分の垂直二等分線だから,y=1 → 図と合わない 2) |z+1|=|z−1+2i|は−1, 1−2iを結ぶ線分の垂直二等分線だから,y=x−1 → 図と合わない 3) |z−1|=|z+1−2i|は1, −1+2iを結ぶ線分の垂直二等分線だから,y=x+1 → 図と一致する 4) |z−1|=|z−1+2i|は1, 1−2iを結ぶ線分の垂直二等分線だから,y=−1 → 図と合わない
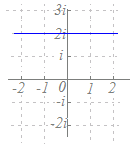
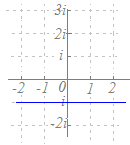
原点と点−2iを結ぶ線分の垂直二等分線になるので,y=−1になります.
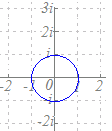
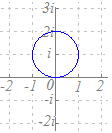
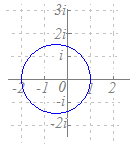
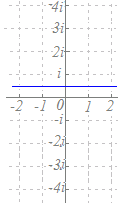
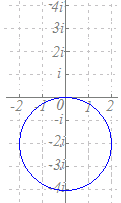
2点2i, −iを結ぶ線分を2:1に内分する点(0)と2:1に外分する点(−4i)を直径の両端とする円だから,−2iを中心とする半径2の円になります.
|
|
式から見ると
1) |z|=2|z−3| → 2点0, 3を結ぶ線分を2:1に内分する点 (2)と2:1に外分する点(6)を直径の両端とする円だから,4を中心とする半径2の円になります.→ 対応しない. 2) |z|=3|z−3| → 2点0, 3を結ぶ線分を3:1に内分する点 ()と3:1に外分する点()を直径の両端とする円だから,を中心とする半径の円になります.→ 対応しない. 3) |z−3|=2|z| → 2点3, 0を結ぶ線分を2:1に内分する点(1)と2:1に外分する点(−3)を直径の両端とする円だから,−1を中心とする半径2の円になります.→ 対応している. 4) |z−3|=3|z−2| → 2点3, 2を結ぶ線分を3:1に内分する点 ()と3:1に外分する点()を直径の両端とする円だから,を中心とする半径の円になります.→ 対応しない. |
|
[注]直前にPC版から入られた場合は,自動転送でスマホ版に来ていますので,ブラウザの[戻るキー]では戻れません(堂々巡りになる).下記のリンクを使ってメニューに戻ってください.
|
|
■[個別の頁からの質問に対する回答][(複素数で表される)軌跡の方程式 について/18.6.13]
コメント失礼しますm(__)m
定点からの距離が一定である点の軌跡のところの、赤字、z=x+yi, α~a+biとして,|z−α|=rを(x, y)座標で表すと,
√(x−a)2+(y−b)2=r
(x−a)2+(y−b)2=r2
となって,数学IIで習う円の方程式と一致する.
しかし,複素数で示された問題を常に(x, y)座標に直して考えていると能率が悪いので,特に行き詰ったときだけ(x, y)座標に直すようにし,複素数の問題は複素数のままで答えるようにするのがよい.
の冒頭、α~a+bi は、 α=a+biなのではないでしょうか?
■[個別の頁からの質問に対する回答][軌跡の方程式について/18.3.22]
=>[作者]:連絡ありがとう.Shiftきーを押しながら,1つ隣のキーを押したようですので,訂正しました. (8)の2の解答の3:1内分する点は9/4ではないのですか?
■[個別の頁からの質問に対する回答][(複素数で表される)軌跡の方程式について/18.3.5]
=>[作者]:連絡ありがとう.訂正しました. 複素数の垂直二等分線の式がダブり?
(x+1)2+y2=(x+1)2+y2
■[個別の頁からの質問に対する回答][軌跡の方程式 について/17.2.18]
=>[作者]:連絡ありがとう.転記ミスですので訂正しました. 私は学生時代部活ばかりしていて、高度な数学知識はありません。中学時代の数学ですら数学として理解してない場合が多い。算数のそろばん時代に戻りたい。
=>[作者]:連絡ありがとう.言っても始まらないことを考えるのは前向きな考えではないので,できることを探しましょう. |