《問題3》
1
△ABCにおいて,sinA:sinB:sinC=5:6:7とする.最大角をθとするとき,cosθ=[ ]である.
(日本工大入試問題からの引用)

|
左の空欄を埋めると,
|
正弦定理によりsinA:sinB:sinC=a:b:c=5:6:7
⇒ a:b:c=5k:6k:7kとおけてcが最大だからCが最大角θになる
cosθ=cosC= . (5k)2+(6k)2−(7k)22·(5k)·(6k)nnnnnnnnnnnnnn= . (5k)2+(6k)2−(7k)22·(5k)·(6k)nnnnnnnnnnnnnn= . 12k260k2nnnn= . 12k260k2nnnn= . 15n 15n
|

2
三角形の3つの高さを各々4,9,6とするとき,最小角の余弦は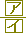 . .

|
左の空欄を埋めると,
|
三辺の長さをa , b , cとおき、各々に対する高さをh1 , h2 , h3といて、面積Sを3通りに表すと辺の長さの比が分かる。
S= . ah12nn= . ah12nn= . bh22nn= . bh22nn= . ch32nn= . ch32nn= . 4a2nn= . 4a2nn= . 9b2nn= . 9b2nn= . 6c2nn 6c2nn
a= . S2n , b= . S2n , b= . 2S9nn , c= . 2S9nn , c= . S3n ⇒ a:b:c=9:4:6 S3n ⇒ a:b:c=9:4:6
bが最小だからBが最小角になる
cosB= . (9k)2+(6k)2−(4k)22·(9k)·(6k)nnnnnnnnnnnnnn= . (9k)2+(6k)2−(4k)22·(9k)·(6k)nnnnnnnnnnnnnn= . 101k2108k2nnnnn= . 101k2108k2nnnnn= . 101108nnn 101108nnn
|

3
△ABCの3辺がBC=x2-x+1,CA=x2-2x,AB=2x-1で表されている.
(1) 3つの辺の大小関係を調べよ.
(1)
(備考)
三角形の成立条件
a>0・・・(1)
b>0・・・(2)
c>0・・・(3)
a+b>c・・・(4)
b+c>a・・・(5)
c+a>b・・・(6)
のうち,(4)(5)(6)から(1)(2)(3)が導かれるので,(例えば(4)(5)の辺々を加えるとc>0となり(3)を得るなど)
三角形の成立条件としては(4)(5)(6)で必要十分です.
三角形の成立条件より
( x2-x+1)+( x2-2x)>( 2x-1)・・<1>
( x2-2x)+( 2x-1)>( x2-x+1)・・<2>
( 2x-1)+( x2-x+1)>( x2-2x)・・<3>
<1><2><3>よりx>2
このとき,
( x2-x+1)-( x2-2x)=x+1>0
( x2-2x)-( 2x-1)=x 2-4x+1の符号から
2<x<2+√3のとき( x2-2x)<( 2x-1)
2+√3<xのとき( 2x-1)<( x2-2x)
( x2-x+1)-( 2x-1)=x2-3x+2=(x-1)(x-2)>0
以上より
2<x<2+√3のとき
( x2-2x)<( 2x-1)<( x2-x+1)
x=2+√3のとき
( x2-2x)<( 2x-1)=( x2-x+1)
2+√3<xのとき
( 2x-1)<( x2-2x)<( x2-x+1)
(2) △ABCの最大の内角はいくらか.
(静岡大入試問題からの一部引用)
|

(1)の結果からどの場合でもa=x2−x+1が最大辺になる
cosA= . (x2−2x)2+(2x−1)2−(x2−x+1)22(x2−2x)(2x−1)nnnnnnnnnnnnnnnnnnnnnnnn (x2−2x)2+(2x−1)2−(x2−x+1)22(x2−2x)(2x−1)nnnnnnnnnnnnnnnnnnnnnnnn
= (分子を展開してから因数分解する)
=. −_x(2x−1)(x−2)2(x2−2x)(2x−1)nnnnnnnnnnnnnn=−. −_x(2x−1)(x−2)2(x2−2x)(2x−1)nnnnnnnnnnnnnn=−. 12n⇒A=120° 12n⇒A=120°
|

 《解説》
《解説》