|
5.�@�Q��n�����x�N�g���ƌ����Ƃ��̑��W���̈Ӗ�
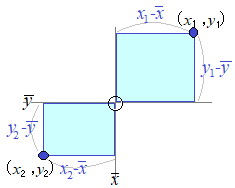
(y_k-\bar{y})\]&chco=0000ff) \( \displaystyle S_{xy}=\sum_{k=1}^n(x_k-\bar{x})(y_k-\bar{y}) \)������ϓ� \( \displaystyle S_{xy}=\sum_{k=1}^n(x_k-\bar{x})(y_k-\bar{y}) \)������ϓ�

�@���ϓ��́C�u���𐬕��Ƃ���x�N�g���v�́u���ρv�ɑΉ�����D
�@���Ȃ킿
&chco=000099) \( \displaystyle \vec{a}=(x_1-\bar{x},\hspace{2px}x_2-\bar{x},\hspace{2px}\cdots,\hspace{2px}x_n-\bar{x}) \) \( \displaystyle \vec{a}=(x_1-\bar{x},\hspace{2px}x_2-\bar{x},\hspace{2px}\cdots,\hspace{2px}x_n-\bar{x}) \)
&chco=000099) \( \displaystyle \vec{b}=(y_1-\bar{y},\hspace{2px}y_2-\bar{y},\hspace{2px}\cdots,\hspace{2px}y_n-\bar{y}) \) \( \displaystyle \vec{b}=(y_1-\bar{y},\hspace{2px}y_2-\bar{y},\hspace{2px}\cdots,\hspace{2px}y_n-\bar{y}) \)
�Ƃ���Ƃ�
(y_1-\bar{y})%2B(x_2-\bar{x})(y_2-\bar{y})%2B&chco=000099) \( \displaystyle \vec{a}\cdot\vec{b}=(x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+ \) \( \displaystyle \vec{a}\cdot\vec{b}=(x_1-\bar{x})(y_1-\bar{y})+(x_2-\bar{x})(y_2-\bar{y})+ \)
(y_n-\bar{y})&chco=000099) \( \displaystyle \cdots+(x_n-\bar{x})(y_n-\bar{y}) \) \( \displaystyle \cdots+(x_n-\bar{x})(y_n-\bar{y}) \)
������C  \( \displaystyle S_{xy}=\vec{a}\cdot\vec{b} \) \( \displaystyle S_{xy}=\vec{a}\cdot\vec{b} \)
 �x�N�g���̑傫���Ŋ���
(y_k-\bar{y})}{\sqrt{\sum_{k=1}^n(x_k-\bar{x})^2}\sqrt{\sum_{k=1}^n(y_k-\bar{y})^2}}\]&chco=0000ff) \( \displaystyle r_{xy}=\frac{\displaystyle \sum_{k=1}^n(x_k-\bar{x})(y_k-\bar{y})}{\sqrt{\displaystyle \sum_{k=1}^n(x_k-\bar{x})^2}\sqrt{\displaystyle \sum_{k=1}^n(y_k-\bar{y})^2}} \)������W�� \( \displaystyle r_{xy}=\frac{\displaystyle \sum_{k=1}^n(x_k-\bar{x})(y_k-\bar{y})}{\sqrt{\displaystyle \sum_{k=1}^n(x_k-\bar{x})^2}\sqrt{\displaystyle \sum_{k=1}^n(y_k-\bar{y})^2}} \)������W��
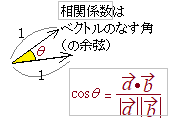
�@���W���́C�u�x�N�g���̂Ȃ��p�v�i�̗]���j�ɑΉ�����D
�@���Ȃ킿
 \( \displaystyle r_{xy}=\frac{\vec{a}\vec{b}}{|\vec{a}|\cdot|\vec{b}|} \) \( \displaystyle r_{xy}=\frac{\vec{a}\vec{b}}{|\vec{a}|\cdot|\vec{b}|} \)
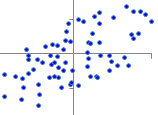
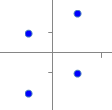
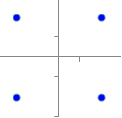
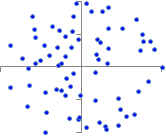
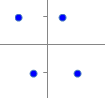
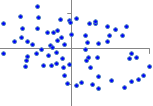
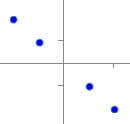
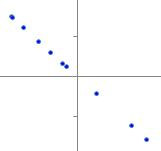
�@���̂悤�ɂ��āC���W����+1�ɋ߂���Q�̃x�N�g���͓��������������Ă���C−1�ɋ߂���Q�̃x�N�g���͋t�����������Ă��邱�ƂɂȂ�D0�ɋ߂���C�Q�̃x�N�g���͖��W�ȕ����������Ă��邱�ƂɂȂ�D

|
�y���5.1�z�@�i���ނ��������j
�@����w���̐��k40�l�ɂ��āC�P�w�����Ԏ����̍���C���w�C�p��̓��_�̑��W���ׂ��D
�@����Ɛ��w�̓��_�̑��W����  \( \displaystyle \frac{\sqrt{3}}{2} \) \( \displaystyle \frac{\sqrt{3}}{2} \)�C���w�Ɖp��̓��_�̑��W����  \( \displaystyle \frac{\sqrt{2}}{2} \) \( \displaystyle \frac{\sqrt{2}}{2} \) �̂Ƃ��C�p��ƍ���̓��_�̑��W���̂Ƃ蓾��l�ׂ͈̔͂Ă��������D
������
�i����j
����̓��_�� ) \( \displaystyle (x_1,\hspace{2px}x_2,\hspace{2px}\cdots,\hspace{2px}x_n) \) \( \displaystyle (x_1,\hspace{2px}x_2,\hspace{2px}\cdots,\hspace{2px}x_n) \)�Ƃ��āC���̕��ς�  \( \displaystyle \bar{x} \) \( \displaystyle \bar{x} \)�ŕ\���C ) \( \displaystyle \vec{x}=(x_1-\bar{x},\hspace{2px}x_2-\bar{x},\hspace{2px}\cdots,\hspace{2px}x_n-\bar{x}) \) \( \displaystyle \vec{x}=(x_1-\bar{x},\hspace{2px}x_2-\bar{x},\hspace{2px}\cdots,\hspace{2px}x_n-\bar{x}) \)�Ƃ����D
���l�ɂ��āC���w�C�p����e�X ) \( \displaystyle \vec{y}=(y_1-\bar{y},\hspace{2px}y_2-\bar{y},\hspace{2px}\cdots,\hspace{2px}y_n-\bar{y}) \) \( \displaystyle \vec{y}=(y_1-\bar{y},\hspace{2px}y_2-\bar{y},\hspace{2px}\cdots,\hspace{2px}y_n-\bar{y}) \)�C
) \( \displaystyle \vec{z}=(z_1-\bar{z},\hspace{2px}z_2-\bar{z},\hspace{2px}\cdots,\hspace{2px}z_n-\bar{z}) \) \( \displaystyle \vec{z}=(z_1-\bar{z},\hspace{2px}z_2-\bar{z},\hspace{2px}\cdots,\hspace{2px}z_n-\bar{z}) \)�Ƃ����D

 \( \displaystyle r_{xy}=\frac{\vec{x}\cdot\vec{y}}{|\vec{x}|\cdot|\vec{y}|}=\frac{\sqrt{3}}{2} \) \( \displaystyle r_{xy}=\frac{\vec{x}\cdot\vec{y}}{|\vec{x}|\cdot|\vec{y}|}=\frac{\sqrt{3}}{2} \)
 \( \displaystyle r_{yz}=\frac{\vec{y}\cdot\vec{z}}{|\vec{y}|\cdot|\vec{z}|}=\frac{\sqrt{2}}{2} \) \( \displaystyle r_{yz}=\frac{\vec{y}\cdot\vec{z}}{|\vec{y}|\cdot|\vec{z}|}=\frac{\sqrt{2}}{2} \)
���W���͕��x�N�g���̂Ȃ��p�i�̗]���j�ł��邩��
 \( \displaystyle \cos\alpha=\frac{\sqrt{3}}{2},\hspace{5px}\cos\beta=\frac{\sqrt{2}}{2} \) \( \displaystyle \cos\alpha=\frac{\sqrt{3}}{2},\hspace{5px}\cos\beta=\frac{\sqrt{2}}{2} \)
�Ƃ����ƁC  \( \displaystyle \vec{y} \) \( \displaystyle \vec{y} \)�ɑ���  \( \displaystyle \vec{x} \) \( \displaystyle \vec{x} \)��  \( \displaystyle \vec{z} \) \( \displaystyle \vec{z} \)�����Α��ɂ���ꍇ�i�}��  \( \displaystyle \vec{x_1} \) \( \displaystyle \vec{x_1} \)�j��  \( \displaystyle \vec{x} \) \( \displaystyle \vec{x} \)��  \( \displaystyle \vec{z} \) \( \displaystyle \vec{z} \)�̂Ȃ��p���ő�Ɂi=���W�����ŏ��Ɂj�Ȃ�C  \( \displaystyle \vec{x} \) \( \displaystyle \vec{x} \)��  \( \displaystyle \vec{z} \) \( \displaystyle \vec{z} \)���������ɂ���ꍇ�i�}��  \( \displaystyle \vec{x_2} \) \( \displaystyle \vec{x_2} \)�j��  \( \displaystyle \vec{x} \) \( \displaystyle \vec{x} \)��  \( \displaystyle \vec{z} \) \( \displaystyle \vec{z} \)�̂Ȃ��p���ŏ��Ɂi=���W�����ő�Ɂj�Ȃ�D
�A�j�@  \( \displaystyle \vec{x_1} \) \( \displaystyle \vec{x_1} \)�̏ꍇ
�C�j�@  \( \displaystyle \vec{x_2} \) \( \displaystyle \vec{x_2} \)�̏ꍇ
�A�j�̏ꍇ�Ɠ��l�ɂ���
=\cos\beta\cos\alpha%2B\sin\beta\sin\alpha) \( \displaystyle \cos(\beta-\alpha)=\cos\beta\cos\alpha+\sin\beta\sin\alpha \) \( \displaystyle \cos(\beta-\alpha)=\cos\beta\cos\alpha+\sin\beta\sin\alpha \)
 \( \displaystyle =\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{2}}{2}+\frac{1}{2}\cdot\frac{\sqrt{2}}{2}=\frac{\sqrt{6}+\sqrt{2}}{4} \) \( \displaystyle =\frac{\sqrt{3}}{2}\cdot\frac{\sqrt{2}}{2}+\frac{1}{2}\cdot\frac{\sqrt{2}}{2}=\frac{\sqrt{6}+\sqrt{2}}{4} \)
���������āC
 \( \displaystyle \frac{\sqrt{6}-\sqrt{2}}{4}\leqq r_{zx}\leqq\frac{\sqrt{6}+\sqrt{2}}{4} \)����i���j \( \displaystyle \frac{\sqrt{6}-\sqrt{2}}{4}\leqq r_{zx}\leqq\frac{\sqrt{6}+\sqrt{2}}{4} \)����i���j
�i�Q�l�j
���̖��ł� ��=30���C��=45���ɂȂ��Ă���C ��+��=75���ƂȂ�ꍇ�ɑ��W�����ŏ��ɂȂ�C ��−��=15���ƂȂ�ꍇ�ɑ��W�����ő�ɂȂ�܂��D
�����適
|









 �i�j
�i�j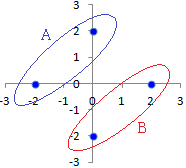
 �i�j
�i�j �i�j
�i�j

 �x�N�g���̑傫���Ŋ���
�x�N�g���̑傫���Ŋ���



