|
■二項分布
【復習】(反復試行の確率)
1回の試行で事象Aが起る確率をpとするとき,この試行をn回繰り返して,事象Aがちょうどr回起る確率は nCr prqn−r
ただし,q=1−pr=0, 1, 2, ..., n−1, n
※この定理は,相互に独立なn回の試行を繰り返す場合を想定して「反復試行の確率」と呼ばれていますが,相互に独立なn個の試行を同時に行う場合にも成り立ち,「独立試行の定理」とも呼ばれます.
【例1】
(解答)10円硬貨を5回投げるとき,表がちょうど2回出る確率 10円硬貨を1回投げて表が出る確率はp= 表が出ない(裏が出る)確率はq=1−p= 試行を5回(n=5)繰り返して,表がr=2回出る確率は 5C2 ()2()3=10×=
【例2】
(解答)正しく作られたさいころは,6回のうち1回の割合で1の目が出るようになっています.このさいころを6回投げたとき,1の目が1回出る確率を求めてください.
6回投げると1の目が「必ず」1回出るという意味に解釈すると,問題が成り立たなくなります.
n=6, r=1, p=, q=を代入
6C1 ()1()5=≒0.40 (半分以下になります)6回投げたときに,1の目から6の目までが完全に1回ずつ出るようなさいころは,正しく作られたさいころではないことは,経験的にも分かるはずです:1の目から5の目までが出たときに,次は「必ず」6の目が出るようになっていれば,それは確率的な動きではなく,「いかさま賭博のさいころ」になります. 6回のうち1回の「割合」で1の目が出るとは,1回の 試行で1の目が出る確率がp=ということです. |
反復試行の確率の公式において,
n=4, r=2, p=, q=を代入
4C2 ()2()2=6×=
→3
【復習問題2】
100円硬貨を10枚同時に投げるとき,少なくとも1枚表が出る確率を求めてください.           (次のうちで最も近い値を選んでください.) 10.9 20.99 30.999 40.9999 50.99999 HELP
独立試行の定理(=反復試行の確率の公式)において,
n=10, r=0, p=, q=を代入すると
全部裏が出る確率は
10C0 ()0()10=
余事象の定理により, (少なくとも1枚表が出る確率)=1−(全部裏が出る確率) を求めると 1−==0.9990234 →3
さいころを1回投げたとき,目の出方{1,2,3,4,5,6}のうちで5以上の目が出るのは{5,6}の2通りだから,反復試行の確率の公式において,
n=3, r=2, p=, q=を代入
3C2 ()2()1=3×=
→2
|
|
【用語と記号】 ○ 1回の試行で事象Aが起る確率がpのとき,n回の反復試行(独立試行)で事象Aが起る回数をXとすると,その確率分布は次の表のようになります.(ただし,q=1−p) この確率分布を二項分布といいます.
(二項分布という名前)
○ 1回の試行で事象Aが起る確率がpのとき,この試行をn回繰り返したときにできる二項分布を二項の和のn乗を展開したときの各項がこの確率になるので,上記の確率分布を二項分布といいます. (p+q)n=nC0 p0qn+nC1 p1qn−1+...+nCn pnq0 B(n, p) で表します.
この記号は,f(x, y)=x2yや5C2=10のような値をあらわすものではなく,単に「1回の試行である事象が起る確率がpであるとき,その試行をn回反復するときに,その事象が起る回数を表す二項分布」ということを短く書いただけのものです.
【例】 B(5, )は,「1回の試行である事象が起る確率が であるとき,その試行を5回繰り返したときに,その事象が起る回数の二項分布」を表します. B(2, )は,「1回の試行である事象が起る確率が であるとき,その試行を2回繰り返したとき,その事象が起る回数の二項分布」を表します. ○ 確率変数Xの確率分布が二項分布になることを,「確率変数Xは二項分布B(n, p)に従う」という言い方をします.
この言い方については,難しく考えずに慣れればよい.
【例3】
確率変数Xが二項分布B(5, )に従うとき,X=3となる確率を求めてください.
例えば,10円硬貨を1回投げたときに,表が出る確率は
5C3 ()3()2=10×()5==
p=で,この試行をn=5回繰り返してちょうどX=3回表が 出る確率を求めることに対応しています.
【例4】
確率変数Xが二項分布B(2, )に従うとき,X=1となる確率を求めてください.
例えば,さいころを1回投げたときに,1の目が出る確率
2C1 ()1()1=2×=
はp=で,この試行をn=2回繰り返してちょうどX=1 回1の目が出る確率を求めることに対応しています.  【例4】 【例4】袋の中に赤玉が3個と白玉が2個とが入っている.よくかき混ぜて,1個取り出し,玉の色を調べてから元に戻すという試行を3回繰り返すとき,赤玉が出る回数Xの確率分布を求めてください.
「確率分布を求めよ」という問題には,確率分布表で答えるとよい.このためには,
n=3 r=0, 1, 2, 3 p= , q=1−= として,r=0からr=3までのすべての値について 3Cr prq3−r の値を求めます.
…(答) |
n=4,r=1,p= , q=1−=として,nCr prqn−r の値を求めます. 4C1()1()3=4××= →4
n=5,r=0,1,2,3,4,p= , q=として,nCr prqn−r の値を求めて,確率分布表を作ります.
表の水色の部分の和を求めると,0≦X≦3となる確 率P(0≦X≦3)は, +++== →4
 【問題3】 【問題3】袋の中に赤玉4個と白玉1個とが入っている.よくかき混ぜて,1個取り出し,玉の色を調べてから元に戻すという試行を3回繰り返すとき,赤玉が出る回数Xの確率分布として正しいものを選んでください.
n=3,r=0,1,2,3,p= , q=として,nCr prqn−r の値を求めて,確率分布表を作ります. →3 |
|
【二項分布の期待値,分散,標準偏差】
確率変数Xが二項分布B(n, p)に従うとき
期待値E(X)=np …(1)
分散V(X)=npq …(2) 標準偏差σ(X)= …(3) ただし,q=1−p
【例5】
1枚の10円硬貨を5回投げるとき,表が出る回数をXと すると,Xは二項分布B(5, )に従います. 確率変数Xの期待値はE(X)=5×==2.5
(平均2.5回だけ表が出るということです)
確率変数Xの分散はV(X)=5××=
確率変数Xの標準偏差はσ(X)==≒1.12
(平均2.5±1.12回の中に7割程度が入ります)

【例6】
(公式の解説)1個のさいころを10回投げるとき,1の目が出る回数をXと すると,Xは二項分布B(10, )に従います. 確率変数Xの期待値はE(X)=10×=≒1.7
(平均約1.7回だけ表が出るということです)
確率変数Xの分散はV(X)=10××=
確率変数Xの標準偏差はσ(X)==≒1.18
(平均1.7±1.18回の中に7割程度が入ります)
 ≪確率の定理だけを使って,簡単に証明する方法≫ (1)←
確率変数の和X+Yの期待値については,X, Yが独立であるか否かに関わらずつねに
確率変数Xが二項分布B(n, p)に従うとき,第r回目の試行で事象Aが起る回数をXrとおくと,Xはそれらの合計になります.E(X+Y)=E(X)+E(Y) が成り立ちます. この関係は,3つの確率変数の和の場合にも成り立ちます. E(X+Y+Z)=E(X)+E(Y)+E(Z) さらに,もっと一般的に,n個の確率変数の和の場合にも成り立ちます. E(X1+X2+...+Xn )=E(X1 )+E(X2 )+...+E(Xn )…(E) X=X1+X2+...+Xn
実際には,Xrは,第r回目の試行で事象Aが起こるときXr=1,起らないときXr=0の2つの値のどちらかになります.
E(Xr)=0·q+1·p=p (E)により E(X)=E(X1)+E(X2)+...+E(Xn)=p+p+...+p=np  (2)← V(Xr)=E(Xr2)−E(Xr)2の公式を使って,V(Xr)を求めます. 上の表により, E(Xr2)=02·q+12·p=p V(Xr)=E(Xr2)−E(Xr)2=p−p2=p(1−p)=pq ここで,各々のXrは「独立」だから,分散について次の公式が使えます. V(X1+X2+...+Xn )=V(X1 )+V(X2 )+...+V(Xn )…(F) したがって V(X)=pq+pq+...+pq=npq (3)← σ(X)== |
(公式の解説) ≪すでに微分を習っている場合≫ 定義に従って,直接計算する方法: (1)← 次の展開式においてxr (r=0,1,2,..,n)の係数がnCr prqn−rになることに着目します.
(px+q)n=
nC0 p0qnx0
+nC1 p1qn−1x1
+nC2 p2qn−2x2
○ (A)においてx=1を代入すると,二項分布の確率分布表において計の欄が1になることが示されます.+...+nCr prqn−rxr+... +nCn−1 pn−1q1xn−1 +nCn pnq0xn…(A)
(p+q)n=
nC0 p0qn
+nC1 p1qn−1
+nC2 p2qn−2
+...+nCr prqn−r+... +nCn−1 pn−1q1 +nCn pnq0 ここでp+q=1だから
nC0 p0qn
+nC1 p1qn−1
+nC2 p2qn−2
+...+nCr prqn−r+... +nCn−1 pn−1q1 +nCn pnq0=1
○ E(X)は,次の式で定義されます. E(X) =0·nC0 p0qn+1·nC1 p1qn−1+...+rnCr prqn−r+...+n·nCn pnq0 そこで,E(X)を求めるために,rnCr prqn−rの形の項を作ることを考えます.そのために,まず(A)の両辺をrで微分します.
n(px+q)n−1p=
0
+1nC1 p1qn−1x0
+2nC2 p2qn−2x1
(B)式においてx=1を代入すると,E(X)の式になります.+...+rnCr pr−1qn−rxr−1+... +(n−1)nCn−2 pn−1q1xn−2 +nnCn pnq0xn−1…(B)
n(p+q)n−1p=
0
+1nC1 p1qn−1
+2nC2 p2qn−2
+...+rnCr pr−1qn−r+... +(n−1)nCn−2 pn−1q1 +nnCn pnq0 ここでp+q=1だから 0+1nC1 p1qn−1 +2nC2 p2qn−2 +...+rnCr pr−1qn−r+... +(n−1)nCn−2 pn−1q1 +nnCn pnq0=np したがって E(X)=np 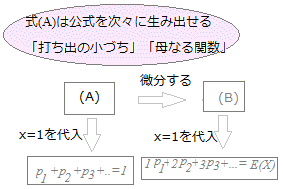
(2)← V(X)=E(X 2)−E(X)2の公式を使って,V(X)を求めるために,まずE(X 2)を計算しておきます. そのためには r2nCr prqn−r の形の式が必要になります.
 ところが,式(B)は
ところが,式(B)はrnCr prqn−rxr−1になっているので,これをさらに微分すると r(r−1)nCr prqn−rxr−2 となってしまって r2nCr prqn−r の形にもっていけません. そこで,(B)の両辺にxを掛けて1次次数を上げてから微分します. (B)の両辺にxを掛けると
np(px+q)n−1x=
0
+1nC1 p1qn−1x1
+2nC2 p2qn−2x2
(C)の両辺を微分すると+...+rnCr pr−1qn−rxr+... +(n−1)nCn−2 pn−1q1xn−1 +nnCn pnq0xn…(C)
np{ (n−1)(px+q)n−2px+(px+q)n−1 }=
(D)式においてx=1を代入すると0+12nC1 p1qn−1x0 +22nC2 p2qn−2x1 +...+r2nCr pr−1qn−rxr−1+... +(n−1)2nCn−2 pn−1q1xn−2 +n2nCn pnq0xn−1…(D)
np{ (n−1)(p+q)n−2p+(p+q)n−1 }=
以上により0+12nC1 p1qn−1 +22nC2 p2qn−2 +...+r2nCr pr−1qn−r+... +(n−1)2nCn−2 pn−1q1 +n2nCn pnq0 ここでp+q=1だから 0+12nC1 p1qn−1 +22nC2 p2qn−2 +...+r2nCr pr−1qn−r+... +(n−1)2nCn−2 pn−1q1 +n2nCn pnq0 =np{ (n−1)p+1 }=n2p2−np2+np E(X 2)=n2p2−np2+np V(X)=E(X 2)−E(X)2=n2p2−np2+np−n2p2 =np−np2=np(1−p)=npq (3)← σ(X)== |
|
n=8, p=, q=だから
E(X)=np=8×=4
V(X)=npq=8××=2
→3
|
【問題5】
1個のさいころを60回投げるとき,5の目が出る回数の期待値と標準偏差を求めてください.(最も近い値を選んでください) 1 期待値10回,標準偏差2.89回 2 期待値10回,標準偏差8.33回 3 期待値50回,標準偏差6.45回 4 期待値50回,標準偏差41.7回 HELP n=60, p=, q=だから E(X)=np=60×=10 V(X)=npq=60××= σ(X)==≒2.89 →1 |
||||||||||||||||
|
この問題は,期待値や分散を求める問題ではなく,個々の確率を求める問題なので,二項分布の確率分布表に戻って考えます.すなわち,次の表においてX=8,9,10となる確率を求めます.
P(X≧8)=45×+10×+1×=≒0.05 →3 |
E(X)=np≧10…(*1) V(X)=σ(X)2=npq≦1…(*2) (*1)(*2)より 10q≦npq≦1 q≦=0.1 したがって,p=1−q≧0.9
実際には,nは整数なので,p=0.9のときに,(*1)(*2)を両立させることはできませんが,
→4たとえばp=0.91のとき, 0.91n≧10より n≧=10.98.. nは整数だから,たとえばn=11のとき np=10.01, npq=11×0.91×0.09=0.90.. となって(*1)(*2)とも成立します. |
||||||||||||||||
|
n回投げて全部裏が出る確率は,nC0()n= 余事象の確率により,少なくとも1回は表が出る確率は1− したがって 1−≧ 1−≧ ≧ 2n≧10 23=8, 24=16だからn≧4 →2
【問題9】
1個のさいころを18回投げるとき,3以上の目が出る回数の期待値と標準偏差を求めてください. 1 期待値6,標準偏差2 2 期待値6,標準偏差4 3 期待値12,標準偏差2 4 期待値12,標準偏差4 HELP さいころを1回投げるとき,目の出方の総数は{ 1,2,3,4,5,6 }の6通り そのうち,3以上の目が出るのは{ 3,4,5,6 }の4通り したがって p=, q= 二項分布B(18, )の
期待値は18×=12
→3分散は18××=4 標準偏差は=2 |
【問題10】
確率変数Xが二項分布B(100, 0.9)に従うとき,Xの期待値と分散を求めてください. 1 期待値10,分散1 2 期待値10,分散3 3 期待値90,分散9 4 期待値90,分散90 HELP E(X)=np=100×0.9=90 V(X)=npq=100×0.9×0.1=9 →3  【問題11】
【問題11】袋の中に赤玉が3個と白玉が2個とが入っている.よくかき混ぜて,1個取り出し,玉の色を調べてから元に戻すという試行を3回繰り返すとき,赤玉が出る回数Xの標準偏差を求めてください. 1 2 3 4 HELP n=3, p=, q=だから V(X)=3××= σ(X)= →2 |