|
■記号と用語 右図1のような「普通のさいころ」1個と,6の目を1の目に書き換えてⅠの目が2つあるように「細工をしたさいころ」1個の合計2個のさいころを投げて,出た目の数を各々X, Yとします.このとき,X, Yの出方に応じて確率を考えるには,右の表1のようにX, Yの確率分布を同時に考えます. このように,2つの確率変数の分布を同時に考えたものを同時確率分布(または同時分布,結合確率分布)といいます. (細工がしてある方のさいころは,1の目が2倍出て,6の目が出ないので,Yの分布は通常のさいころとは異なっています.)
同時確率分布においては,X, Yのすべての値の組に対して確率を考えます.例えば,表1において桃色の背景色で示したものは, X=2, Y=1となる確率がであること すなわち P(X=2, Y=1)= となることを表しています. 水色の背景色で示した数字は,周辺分布と呼ばれ,例えばX=1の右端にある欄は,X=1でYがすべての値をとるときの確率の合計になっています.このようにして,右の欄はYの値が何であるかを問わずにXの値だけを指定したときの確率を表しています. これに対して,下端の水色の背景色で示した数字は,Xの値が何であるかを問わずにYの値だけを指定したときの確率を表しています. 一般に,同時確率分布および周辺分布は,次の表3のような表で表され, P(X=xi , Y=yj )=pijは同時確率分布を表し, P(X=xi )=pi·がXの周辺分布を P(Y=yj )=p·jがYの周辺分布を表しています. 周辺分布は,pi· , p·jのように,ドットを付けて表し, 例えば P(X=x1 )=p11+p12+…+p1n=p1· P(Y=y1 )=p11+p21+…+pm1=p·1 などとなります.
E(X)=x1 p1·+x2 p2·+…+xm pm· E(Y)=y1 p·1+y2 p·2+…+yn p·n と表されることになります. |
図1
表2
下に示した1クラス40人の生徒の身長・体重の「クロス集計表」(左の表)とそれを「同時確率分布」(右の表)に直したものを見比べて,周辺分布が同時確率分布の和になることを理解してください. すなわち P(X=xi )=pi1+pi2+…+pin=pi· P(Y=yj )=p1j+p2j+…+pmj=p·j などが成り立つのは,クロス集計表で各行,各列の小計を周辺和に書くという約束事をそのまま総数(この例では40)で割って確率で書いたものです. この事情の説明には,この他には何もむずかしい定理を使っていません.
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
次の表で与えられる同時確率分布について,以下の問題1〜6に答えてください.
(表の見方に慣れるための問題)
【問題1】 表中の同時確率p13 , p21 , p22 , p23および周辺確率p2· , p·2の値を求めてください. 1 p13=0.1 , p21=0.1 , p22=0.1 , p23=0.2 p2·=0.4 , p·2=0.3 2 p13=0.1 , p21=0.1 , p22=0.2 , p23=0.1 p2·=0.4 , p·2=0.3 3 p13=0.1 , p21=0.1 , p22=0.1 , p23=0.2 p2·=0.3 , p·2=0.4 4 p13=0.1 , p21=0.1 , p22=0.2 , p23=0.1 p2·=0.3 , p·2=0.4 解説
P(X)の周辺確率について,0.6+p2·=1だから
p2·=0.4 (1 2のいずれかに絞られる) P(Y)の周辺確率について,0.5+p·2+0.2=1だから p·2=0.3 同時確率も次にように求まる 0.4+0.1+p13=0.6だからp13=0.1 0.4+p21=0.5だからp21=0.1 0.1+p22=0.3だからp22=0.2 0.1+p23=0.2だからp23=0.1 →2 |
E(X)=1×0.6+2×0.4=1.4
→3
E(Y)=1×0.5+2×0.3+3×0.2=1.7 E(Y 2)=1×0.5+4×0.3+9×0.2=3.5 だから V(Y)=E(Y 2)−E(Y) 2=3.5−1.72=3.5−2.89=0.61 →2 |
|
■X+Yの期待値E(X+Y) 表1のような同時確率分布と表2のようなX+Yの値が与えられたときに,X+Yの期待値を求めるためには,すべてのi , jに対して,(xi+yj )pijを求めて,足すことになります. 具体的には E(X+Y)=2×+3×+…+6× +3×+4×+…+7× +…… +7×+8×+…+11× = となります. このような計算は,非常に込み入っていて大変なので,もっと簡単に計算する方法として,次の公式が利用できます.
X, Yが独立であるかどうかに関係なく,つねに
【例】E(X+Y)=E(X)+E(Y)…(1) が成り立つ. 上の表1,表2で与えられる確率変数X, Yについては E(X)=1×+2×+…+6×== E(Y)=1×+2×+…+5×== だから E(X+Y)=E(X)+E(Y)=+= で求めることができます. |
(1)の証明 E(X+Y) =(x1+y1)p11+(x1+y2)p12+(x1+y3)p13+…+(x1+yn)p1n +(x2+y1)p21+(x2+y2)p22+(x2+y3)p23+…+(x2+yn)p2n +………… +(xm+y1)pm1+(xm+y2)pm2+(xm+y3)pm3…+(xm+yn)pmn =x1(p11+p12+p13+…+p1n) +x2(p21+p22+p23+…+p2n) +………… +xm(pm1+pm2+pm3+…+pmn) +y1(p11+p21+p31+…+pm1) +y2(p12+p22+p32+…+pm2) +………… +yn(p1n+p2n+p3n+…+pmn) =x1p1·+x2p2·+……+xmpm·+y1p·1+y2p·2+……+ynp·n =E(X)+E(Y) さらに,一般に次の関係が成り立ちます.
a, bが定数であるとき,X, Yが独立であるかどうかに関係なく,つねに
E(aX+bY)=aE(X)+bE(Y)…(2) X, Y, Zが独立であるかどうかに関係なく,つねに E(X+Y+Z)=E(X)+E(Y)+E(Z)…(3) |
||||||||||||||||||||||||||||||||||||
|
【例題1】
大中小3個のさいころを同時に投げるとき,出た目の和の期待値を求めてください.
さいころ2個までなら一覧表を作って調べることができますが、3個になると場合分けが多過ぎて大変です.そこで,3つの変数の和の期待値の定理を利用して求めます.
大中小のさいころの出た目を各々X, Y, Zとおくと,
=(1+2+3+4+5+6)== Y, Zについても同様に E(Y)=E(Z)= となるから E(X+Y+Z)=E(X)+E(Y)+E(Z)=×3=…(答)
正しい番号を選択してください.
E(X)=3, E(Y)=2 → E(2X+Y)=2E(X)+E(Y)=6+2=8
→4
|
E(X)=0×+1×= Y, Zも同様だから E(X+Y+Z)=E(X)+E(Y)+E(Z)=++==1.5 →2
E(X)=0×+1×+2×+3×= しかし,この問題は上の答案のように,1枚ずつの期待値の和としても求めることができるということです.
【問題6】
100円硬貨と500円硬貨を1枚ずつ合計2枚同時に投げて,表を向いた硬貨をもらえることにするとき,もらえる金額の期待値を求めてください. 1300円 2400円 3500円 4600円 解説
表を向く100円硬貨の枚数をX (X=0, 1),表を向く500円硬貨の枚数をY (Y=0, 1)とすると
E(X)=E(Y)= もらえる金額は100X+500Yだから E(100X+500Y)=100E(X)+500E(Y)=+=300 →1
|
|
【要点】
(解説)[和差の期待値] X, Yが独立であるかどうかに関係なく,つねに E(X+Y)=E(X)+E(Y)…(1)再掲 E(X−Y)=E(X)−E(Y)…(1’) [積の期待値] X, Yが独立であるとき E(XY)=E(X)E(Y)…(4) [和差の分散] X, Yが独立であるとき V(X+Y)=V(X)+V(Y)…(5) すなわち σ2=σx2+σy2…(6) ただしV(X−Y)=V(X)+V(Y)に注意 (1’)← (2)式のE(aX+bY)=aE(X)+bE(Y)において,a=1, b=−1とおくと E(X−Y)=E(X)−E(Y) (4)←
≪2つの確率変数X, Yの独立の定義≫
上の定義により,X, Yが独立であるとき,同時確率分布および周辺分布は次のようになります.すべてのi, jについて P(X=xi , Y=yj )=P(X=xi )P(Y=yj ) が成り立つとき,すなわち pij=pi·p·j が成り立つとき,確率変数X, Yは独立であるという.
※ 独立 ⇔ 各々の同時確率が周辺確率の積になる
=x1 y1 p1· p·1+x1 y2 p1· p·2+…+x1 yn p1· p·n +x2 y1 p2· p·1+x2 y2 p2· p·2+…+x2 yn p2· p·n +………… +xm y1 pm· p·1+xm y2 pm· p·2+…+xm yn pm·p·n =x1 p1· (y1 p·1+y2 p·2+…+yn p·n ) +x2 p2· (y1 p·1+y2 p·2+…+yn p·n ) +………… +xm pm· (y1 p·1+y2 p·2+…+yn p·n ) =(x1 p1·+x2 p2·++…+xm pm· )(y1 p·1+y2 p·2+…+yn p·n ) =E(X)E(Y)
【例】
次の表のように,どの列(縦の並び)についても比率が同じで,どの行(横の並び)についても比率が同じになるときに,独立であるといえます.
縦の並びが同じ比率⇒Yに関係なくXの比率が同じ:XはYから独立 |
(5)← V(X)=E(X 2)−E(X)2の公式により V(X+Y)=E((X+Y)2)−E(X+Y)2 ここで(1)により E((X+Y)2)=E(X 2+2XY+Y 2) =E(X 2)+2E(XY)+E(Y 2) はつねに成立します. また(1)により E(X+Y)2=E(X+Y)E(X+Y)=(E(X)+E(Y))2 =E(X)2+2E(X)E(Y)+E(Y)2 もつねに成立します. したがって V(X+Y)=E(X 2)−E(X)2 +E(Y 2)−E(Y)2 +2E(XY)−2E(X)E(Y) =V(X)+V(Y) +2E(XY)−2E(X)E(Y) X, Yが独立であるときは,E(XY)=E(X)E(Y)だから V(X+Y)=V(X)+V(Y) が成り立ちます.
V(XY) = V(X)V(Y)ではないことに注意
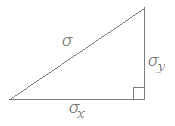 (5)式は,分散の代わりに標準偏差で表すと (5)式は,分散の代わりに標準偏差で表すと
V(X+Y)=σ2
のときに,三平方の定理(ピタゴラスの定理)が成り立つことを示しています.V(X)=σx2 V(Y)=σy2
σ2=σx2+σy2
☆独立とは無関係,無相関,直角ということ☆
次の同時確率分布で与えられる確率変数X, Yが独立であるとき,以下の問題7〜9に答えてください.
周辺確率の和から 0.6+0.3+p·3=1 p·3=0.1 →1 確率変数X, Yが独立であるから,同時確率は周辺確率の積に等しい. p11=p1·×p·1=0.7×0.6=0.42 →4 まず,周辺確率の和の性質から 0.7+p2·=1 p2·=0.3 また,問題7の結果から p·3=0.1 次に,確率変数X, Yが独立であるから,同時確率は周辺確率の積に等しいから p23=p2·×p·3=0.3×0.1=0.03 →2 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
【問題10】
右図のような「普通のさいころ」1個と,6の目を1の目に書き換えてⅠの目が2つあるように「細工をしたさいころ」1個の合計2個のさいころを投げて,出た目の数を各々X, Yとします.このとき,出た目の積XYの期待値を求めてください. 1 2 7 3 4 解説 E(X)=1×+2×+3×+4×+5×+6× =(1+2+3+4+5+6)== E(Y)=1×+2×+3×+4×+5× =(2+2+3+4+5)== X, Yは独立だから E(XY)=E(X)E(Y)== →3 もちろん,同時確率のすべての値についてXY×pXYの和を求めてもできる. E(XY)=1×+2×+… +2×+4×+… +…… +6×+12×+…+30×= しかし,このような計算は非常に長くなるため,上記の答案のように独立な変数X, Yの期待値を別々に求めて,それらの積を計算すればよい. |

|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
独立な確率変数X, Yの期待値および標準偏差が次の表のように与えられているとき,以下の問題11〜14に答えてください.
V(X)=σX2
V(aX)=a2V(X)
V(X)=E(X 2)−E(X)2
確率変数X, Yは独立だから E(XY)=E(X)E(Y)=3×7=21
→4V(X)=E(X 2)−E(X)2
によりE(X 2)=V(X)+E(X)2=σX2+mX2
=12+32=10
→3 |
V(aX)=a2V(X)
によりV(2Y)=22V(Y)=22σY2
=4×4=16
→4
確率変数X, Yは独立だから
V(X+Y)=V(X)+V(Y)
=σX2+σY2
=1+4=5
→2 |
 Y
Y