|
【分散】
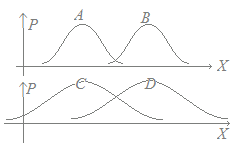
(解説)期待値(平均値)をmとするとき,データの散らばり具合を表す値:分散Vは,次の式で定義されます. V=…(1) 表1のような度数分布表で表される場合は,xkがfkずつあるから,各々の変数を取る確率で表せば V=(x1−m)2+(x2−m)2+…+(xn−m)2 表3のように確率分布表になっている場合には V=(x1−m)2p1+(x2−m)2p2+…+(xn−m)2pn…(2) 【標準偏差】 標準偏差は分散の正の平方根(ルート)で定義されます. σ=…(3) 【分散と2乗平均の関係】 分散は,元の変数の(2乗の平均)−(平均の2乗)に等しくなります. V=E(X 2)−E(X)2…(4) (※現在では,コンピュータを利用することが多いので,分散の計算は元の定義式(1)のままで行うことができます.筆算で行う場合や様々な関係式を証明するためには,(4)も必要になります.) ○ 平均値E(X)という1種類の代表値だけでは,元のデータの散らばり具合が表せません. 次の図1の上の図と下の図とでは,平均値が同じですが,上の図ではデータが平均値付近に集まっているのに対して,下の図ではデータは散らばっており,これら2つのデータは異なる傾向を持っています.
また,AとBとでは,散らばりが等しく,平均値はBの方が大きくなっています. AとD,BとCでは平均値も散らばりも異なっています. ○ データの散らばり具合を表す数字が分散V(X)(または標準偏差σ(X))です.
散らばり具合を数値で表すために,それぞれの値xkが平均値mからどれだけ離れているか:偏差xk−mの平均を取ることが考えられますが,(*A)に示すように偏差を単純に平均すると0になっていしまい,散らばり具合を区別することはできません.
次に,負となる偏差の符号を変えて,偏差の絶対値|xk−m|の平均を取ったものを使うと,散らばり具合を表すことができますが(平均偏差),(*B)に示すように変形が煩わしく,扱いにくい式になるため,実際にはあまり使われません. 散らばり具合を表すことができて,実際の計算も行いやすいものとして,偏差の2乗(xk−m)2の平均で定義される分散というものが使われます. 期待値(平均値)をmとするとき,分散Vは,次の式で定義されます. V= (xk≧mの場合でも,xk<mの場合でも,いずれも2乗すると0以上となって,xkが平均値mからの離れるほど分子の各項は大きくなります.) 表1のように度数分布表で示され,同じ値が各々f1個,f2個,...全部でN個ある場合,分散は V= =(x1−m)2+(x2−m)2+...+(xn−m)2 表3のように =pk (k=1,2,3,...,n)とおくと, 分散は V=(x1−m)2p1+(x2−m)2p2+...+(xn−m)2pn 右に続く→
|
表1(度数分布表)
表2(確率分布表)
 =pkとおく =pkとおく表3(確率分布表)
▼(*A) 単純に平均値との差を取ったもの:xk−mを平均しても,正負で打ち消し合って消えてしまうので使えない.
[例] 次の例では,平均値はm=0となっている.
 =0
このように平均値との差xk−mの平均を調べても,0になってしまって,役に立たない.
▼(*B) また,平均値との差の絶対値 |xk−m|の平均(平均偏差)は,散らばりを表現する目的には最適に見えるが,変形しにくく,扱いにくいのが最大の難点
|x+a|+|x+b|や(|x+a|+|x+b|)2 のような式は簡単には変形できない.  平均偏差はめったに使われない.
◎(*C) そこで,平均値との差の2乗(xk−m)2の平均:分散V(X)と呼ばれるものを使う.
→続き
上の例では
(分散)=
元の数が負の数であっても,正の数であっても,2乗するとすべて正の数に変わる所がミソ.さらに「変形が簡単」にできる長所がある.
(注) 分散は元の変数の2乗を使っているので,元の変数が cm のとき,分散の単位は cm2 となり,単位は合わない. 分散V(X)は非常によく使われるが,元のスケールに揃えて見るときには,分散の正の平方根(ルート)をとった標準偏差σ(X)が用いられる. ○ 分散は偏差を2乗しているので,元の変数xkと単位がそろっていません.元の変数xkと同じ単位の数字として,分散の正の平方根(ルート)で定義される標準偏差が使われます. σ= (4)の証明
分散を計算するためには,先に平均値を求めておきます. m= 次に,この平均値を使って,分散を計算します. V=…(1) (1)式の分母を変形すると (x1−m)2+(x2−m)2+(x3−m)2+…+(xN−m)2 =(x12+x22+…+xN2)−2m(x1+x2+…+xN)+Nm2 したがって分散は V=−2m+m2 =−2m2+m2 =−m2 =−( )2 ここで,xk2の平均:をE(X 2)で, xkの平均:をE(X)で表すと V=E(X 2)−E(X)2 ※度数分布表や確率分布表で示される場合にも,この関係は成り立ちます. |
|
【例1】
1個のさいころを投げるとき,出る目の分散と標準偏差を求めてください.
分散を求めるためには,先に期待値を計算しておかなければなりません.
(解答)確率分布表は次のようになる.
m=(1+2+3+4+5+6)= 分散は V={ (1−)2+(2−)2+(3−)2+...+(6−)2 } ={ ()2+()2+()2+...+()2 } ={ } = 標準偏差は σ===
(参考)
散らばりを表す標準偏差σの値は,平均値mから一番遠い値までの距離ではなく,(多くの場合に)m±σの範囲に変数の約70%(詳しくいえば68.5%)程度が入るような値になっています. ⇒ σまで取れば,7割程度が含まれる. 
コンピュータを使わずに分散を計算するときは,V=E(X 2)−E(X)2の公式を使う方が簡単になります.
そのためには,まず次の表を作ってE(X 2)を求めます.
したがって V=E(X 2)−E(X)2=−()2=−= |
【例2】
5枚の硬貨を同時に投げるとき,表が出る枚数の分散と標準偏差を求めてください.
分散を求めるためには,先に期待値を計算しておかなければなりません.
(解答)5枚の硬貨を投げて,表がr枚出る確率は, 5Cr()r()5−r=()5だから 確率分布表は次のようになる.
E(X)=0×+1×+2×+3×+4×+5×= 分散は V=(0−)2+(1−)2+...+(5−)2 =++...+== 標準偏差は σ==
V=E(X 2)−E(X)2の公式を使う場合は
まず次の表を作ってE(X 2)を求めます.
したがって V=E(X 2)−E(X)2=−()2=−= |
|
正しい番号を選択してください.
(玉の出方は2種類しかない)
(解答)5個ある玉の中から,3個取り出す方法は,全部で N=5C3=10通り ア) 赤玉2個と白玉1個を取り出す方法は 4C3×1C1=6通り イ) 赤玉3個と白玉0個を取り出す方法は 4C3×1C0=4通り したがって,赤玉の個数について,確率分布表は次のようになる.
m=2×+3×= 分散は, V=(2−)2×+(3−)2× =+== →3
V=E(X 2)−E(X)2の公式を使う場合は
まず次の表を作ってE(X 2)を求めます.
したがって V=E(X 2)−E(X)2=6−()2=6−= |
 【問題2】 【問題2】トランプのハートのカードが3枚,スペードのカードが4枚,合計7枚ある.裏返してよく切ってから,1枚ずつ2回抜き取るとき,ハートのカードが出る回数の標準偏差を求めてください.ただし,抜き取ったカードは元に戻さないものとします. 1 2 3 4 HELP
期待値→分散→標準偏差の順に求めます
7枚のカードから,カードを1枚ずつ2回取り出す(元に戻さない)方法は,全部でN=7×6=42通り ア) スペード,スペードの順に出る出方は 4×3=12通り イ) スペード,ハートまたはハート,スペードの順に出る出方は 4×3+3×4=24通り ウ) ハート,ハートの順に出る出方は 3×2=6通り したがって,ハートが出る回数について,確率分布表は次のようになる.
m=0×+1×+2×= 分散は V=(0−)2×+(1−)2×+(2−)2×== 標準偏差は σ== →1
V=E(X 2)−E(X)2の公式を使う場合は
次の表によりE(X 2)とE(X)を求めます.
E(X 2)=0×+1×+4×= したがって V=E(X 2)−E(X)2=−()2= |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
4枚の10円硬貨を同時に投げるとき,表がr (r=0,1,2,3,4)枚出る確率は,
4Cr()r()4−r=()4 V=E(X 2)−E(X)2の公式を使う場合, 次の表によりE(X 2)とE(X)を求めます.
E(X 2)=0×+1×+4×+9×+16×==5 したがって V=E(X 2)−E(X)2=5−22=1 →2
|
【問題4】
2個のさいころを投げて,出た目の差(出た目の大きい方から小さい方を引くものとし,出た目が等しいときは差は0とする)の分散に最も近い値は次のどれになるか. 11.1 22.1 33.1 44.1 HELP
出た目の差は次の表のようになる.
次の表によりE(X 2)とE(X)を求めます.
=≒1.94 E(X 2) =0×+1×+4×+9×+16×+25× =≒5.83 したがって V=E(X 2)−E(X)2=5.83−1.942=5.83−3.78=2.05 →2 分散の定義式のまま計算すると,かなり複雑な分数計算になります. |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
上の表により E(X)=0×0.1+1×0.4+2×0.4+3×0.4=0.4+0.8+0.3=1.5 E(X 2)=0×0.1+1×0.4+4×0.4+9×0.4=0.4+1.6+0.9=2.9 したがって V=E(X 2)−E(X)2=2.9−1.52=2.9−2.25=0.65 →4
|
2枚の10円硬貨を投げたときに,表がr枚出る確率は
2Cr()r()2−r=2Cr()2= となるから ア) 表が2枚,裏が0枚出る確率は イ) 表が1枚,裏が1枚出る確率は ウ) 表が0枚,裏が2枚出る確率は 確率分布表は,次のようになる.
E(X)=(−2)×+0×+2×=0 E(X 2)=0×+4×=2 したがって V=E(X 2)−E(X)2=2 σ== →2
|

 【問題1】
【問題1】
