|
1.�@��\�l
�@�����̓������P�̐����ŕ\�����̂���\�l�Ƃ����D�@��\�l�̒��ōł��d�v�Ȃ��̂����ϒl�ŁC���̑�\�l�Ƃ��Ă������l�C�ŕp�l�Ȃǂ�����D
�p��Ō����C���ϒl(mean)�C�����l(medium)�C�ŕp�l(mode)����S��m�Ȃ̂�M�����ł́C�ǂꂩ������� �� Me , Mo�ȂǂƏ���
(1.1)�@���ϒl�@���������C�Z�p�����͒P�����ϒl�������������ƌĂ�C�قƂ�ǂ̓��v�ő�\�l�Ƃ��ĕ��ϒl���p������D
(1)�@n�̕ϐ�
�Œ�`�����D (2)�@���������̂悤�ȓx�����z�\�ŗ^�����Ă���Ƃ��C
|
1)�@(1)�̒�`�́C�u�e�X�̎����̊m���i���d�j�����v�u�m���̑��a��1�v�Ƃ������̂ɂȂ��Ă���D
��������M1
2)�@���������̂悤�ȓx�����z�\�ŗ^�����Ă���Ƃ��C���敽��M0 ���a����M−1 2�敽��M2 ����ʂɁCM−1��M0��M1��M2�����藧��
�@���̎������P���������ꍇ�Ɠx�����z�\����v�Z�����ꍇ�Ƃł́C������͍��ق����邪�C�ʏ�C���̍��ق͖����ł�����̂ƌ��Ȃ��D 3)�@���ϒl�i�Z�p���ρj�ȊO�̑�\�l���g�����Ƃ��āC�u���Z�C���Ă����Z�v�łR��̎��Z�̂����ōő�l���\�l�Ƃ���C�u�̑����Z�v�ŕ]���̍ő�l�ƍŏ��l���������c��̕��ϒl���\�l�Ƃ��邱�ƂȂǂ�����D |
 �i����j
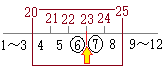
�i����j �@�R�̎����̏ꍇ�C�ȏ���@�j�`�C�j���番����悤�ɁC
�@�R�̎����̏ꍇ�C�ȏ���@�j�`�C�j���番����悤�ɁC �@11�̎����̒����l�́C�����������珇�ɐ�����5�Ԗڂ̒l�ɂȂ�D
�@11�̎����̒����l�́C�����������珇�ɐ�����5�Ԗڂ̒l�ɂȂ�D (3)�@�P��`�ȊO�ŁC�o��`�C����`�C��l���z�Ȃǂ̏ꍇ�C�u�ŕp�l�͊�������Č��܂�Ȃ��v�ƌ����ꍇ������C�u�ŕp�l�͂Ȃ��v�Ƃ����ꍇ�����邪�C�P��`�ȊO�̕��z�ł́C�ŕp�l���l���Ă����܂�Ӗ����Ȃ��Ȃ����Ƃ������D
(3)�@�P��`�ȊO�ŁC�o��`�C����`�C��l���z�Ȃǂ̏ꍇ�C�u�ŕp�l�͊�������Č��܂�Ȃ��v�ƌ����ꍇ������C�u�ŕp�l�͂Ȃ��v�Ƃ����ꍇ�����邪�C�P��`�ȊO�̕��z�ł́C�ŕp�l���l���Ă����܂�Ӗ����Ȃ��Ȃ����Ƃ������D
 �i����j
�i����j �@��L��B�̂悤�Ɋ��S�ɍ��E�Ώ̂̏ꍇ�́C���ϒl=�����l=�ŕp�l�ł��邪�C�������E�ɃY���Ă���ꍇ�C�u���ϒl�́C�O��l����O�e�[���Ɉ��������₷���C�q���ɔ�������v�������l�́C�����ɍ��E����ɂ����D
�@��L��B�̂悤�Ɋ��S�ɍ��E�Ώ̂̏ꍇ�́C���ϒl=�����l=�ŕp�l�ł��邪�C�������E�ɃY���Ă���ꍇ�C�u���ϒl�́C�O��l����O�e�[���Ɉ��������₷���C�q���ɔ�������v�������l�́C�����ɍ��E����ɂ����D