二項分布

■二項分布
【要約】
　確率変数 X が二項分布 B(n, p) に従うとき，q = 1 - p とすると

期待値は　E(X) = np　･･･(1)
分散は　V(X) = npq　･･･(2)
標準偏差は　σ(X) = 　　･･･(3)

例１
1枚の硬貨を10回投げるとき，表の出る回数の期待値と標準偏差を求めよ．
（答案）

E(X) = 10× = 5

σ(X) = =

例２さいころを360回投げたとき，１の目の出る回数の期待値と分散を求めよ。
（答案）

E(X) = 360× = 60

V(X) = 360×× = 50

【要約】･･･二項分布の正規分布による近似

　ｎが十分大きいとき，二項分布 B(n, p) は，正規分布 N(np, npq) で近似できる．　　･･･(4)
（※np > 5 かつ nq > 5 を満たせば「十分大きい」とみなしてよいとされている(*1)．実際上，二項分布として直接計算するのが大変な大きなnについては，正規分布と見なして求めるとよい．）

例３
1枚の硬貨を400回投げるとき，表が230回以上出る確率を求めよ．なお，次の正規分布表を利用してよい．

u	1	2	3
p(u)	0.3413	0.4772	0.4987

（答案）

m = 400× = 200

V(X) = = 100，σ(X) = 10

P(X≧ 230) = P(X≧ m + 3σ)を正規分布で近似すると，0.5-0.4987=0.0013

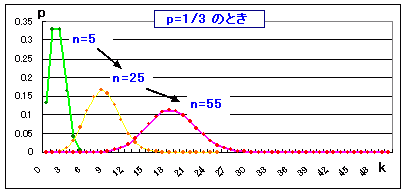
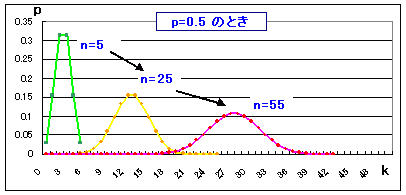
■まったくの初心者向け■

【二項分布の簡単な例】　

　１個のさいころを1回投げて１の目が出る確率は，

　このとき，さいころを5回投げたとき1の目が2回出る確率は

10 ()2()3

　一般に，さいころを5回投げたとき1の目がk回出る確率は

5Ck()k()5-k

そこで，「さいころを5回投げたとき１の目が出る回数 X を確率変数とするとき， X の確率分布」は次のようになる．

X の期待値は，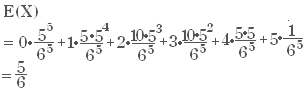

分散は，E(X²) - E(X)²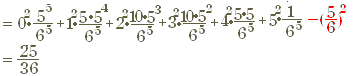

5回の内１が2回出るのは，

(1)(1)(1以外)(1以外)(1以外)　→　()2()3

(1)(1以外)(1)(1以外)(1以外)　→　()2()3

(1)(1以外)(1以外)(1)(1以外)　→　()2()3

(1)(1以外)(1以外)(1以外)(1)　→　()2()3
･･･
(1以外)(1以外)(1以外)(1)(1)　→　()2()3

のいずれでもよい．5回の内1の目が出る番号を２つ選ぶ方法は
5C2 = = 10 通りあるから，

結局，さいころを5回投げたとき1の目が2回出る確率は

10 ()2()3

　上の例から分かるように，１回の試行で事象Aの起こる確率がpのとき，この試行をn回行って事象Aがk回起こる確率は， q = 1 - p として nCk pkqn-k となる．

【二項分布とは】
　１回の試行で事象Aの起こる確率がp のとき，この試行を n 回行ったときに事象Aが起こる回数をXとおくとき，Xは確率変数となり， P(X=k) = nCk pkqn-k
となる．このような確率分布を二項分布といい， B(n, p) で表わす．

※　二項分布は次のような確率分布となる．

X	0	1	…	k	…	n	計
P	nC0qn	nC1p1qn-1	…	nCkpkqn-k	…	nCnpn	1

※　二項分布の記号B(n, p) は，「１回の試行でその事象が起こる確率がp である試行を n 回繰り返したときの二項分布 (Binomial distribution) 」と言葉で書くことを記号で書いたものと考えればよく，この記号に関数としての値を考えることはない．
　同様に，正規分布の記号N(m, σ2) は，「期待値が m，分散がσ2の正規分布 (normal distribution)」と言葉で書くことを記号で書いたものと考えればよく，この記号に関数としての値を考えることはない．
→　二項分布の記号 B(試行回数，１回当りの成功確率)
→　正規分布の記号 N(期待値，分散)

【なぜ二項というか？】
　この確率分布関数　nCk pkqn-k　が二項の和のn乗　(p + q)n の展開式となっているからである．

【公式の解説】
(1)←
　１回の試行で事象Ａが起こる確率がpとなる試行をn回繰り返すとき，
第k回で事象Ａが起これば1，起こらなければ0となる確率変数Xkを用いると　（*「確率変数の変換」参照）
E(Xk) = 0･q + 1･ p = p （ k = 1,2,…,n ）
V(Xk) = E(Xk2) - E(Xk)2= 02･ q + 12･ p - p2
= p - p2 =p(1 - p) = pq
（ k = 1,2,…,n ）
E(X) =E(X1)+E(X2)+ … +E(Xn) = np
(2)←
　各回の試行は独立である（お互いに影響されない）から，
V(X) =V(X1)+V(X2)+ … +V(Xn) = npq
(3)←
標準偏差は分散の正の平方根だから明らか．
(4)←
ここでは，数学的な解説は省略するが，まず次の例から，ｎが大きくなると「左右対称になる」「なめらかな富士山型に近づく」ことを視覚的につかむことが大切．

［参考］
　高校の今の教育課程で，二項係数(_nC_k)の和の性質を教えることはめったにない･･･「組合せ」（数学Ａ）を済ませてかつ時間に余裕がある受験系，数学Ｃを選択しかつその学校が確率分布を扱いかつ時間に余裕がある場合など

f(x) = (x + 1)ⁿ とおくと
f(x) = _nC₀ + _nC₁x +_nC₂x² + ･･･+_nC_nxⁿ だから
f(1)=_nC₀ + _nC₁ +_nC₂ + ･･･+_nC_n=2ⁿ･･･(1)

次に，各々の_nC_kに異なる数kを掛けるには，微分するとちょうどkが掛けられることを利用して
f’(x)=n(x+1)^n-1= _nC₁ +2_nC₂x + ･･･+n_nC_nx^n-1 だから
xf’(x)=nx(x+1)^n-1= _nC₁ x+2_nC₂x² + ･･･+n_nC_nxⁿ　･･･(2)
x=1を代入すると
_nC₁ +2_nC₂ + ･･･+n_nC_n =n2^n-1

さらに(2)を微分して両辺にxを掛けるなどの変形により二項係数(_nC_k)の和の性質を用いて，E(X) ,V(X)を求めることができるが，計算量はかなり多くなる．

【Excelで二項分布を求めるには？】
　→　二項分布とは上の水色で示したような表（各々の確率変数 X の値に対する確率の対応表）なので，Excelでは各々の X の値に対して nCk pkqn-k を計算すればよい．
この目的のためには，関数 BINOMDIST(成功数，試行回数，成功率，関数形式) が使える．
　例えば，1つの値 10C4 0.340.76 を計算するには，その値を書き込みたいセルに直接 = BINOMDIST(4,10,0.3,0)と書き込むか，または，メニューから「挿入」→「関数」→「統計」→BINOMDIST として

成功数として4（または４が書き込まれたセル）
試行回数として10（または10が書き込まれたセル）
成功率として0.3（または0.3が書き込まれたセル）
４番目の引数に0を指定すればよい．

（※筆者の手元にある関数マニュアルでは関数形式：4番目の引数は省略可能とされているが，筆者のEXcel 2002 では4番目の引数を省略するとエラーになり省略はできない．この引数に TRUE または1を指定すると累積分布関数となり， FALSE または0を指定すると確率分布関数となる．ここでは確率分布関数がほしいのだから0を指定する．）

B(5, 0.3) の例
　この表を作成するには，B3において=BINOMDIST(B2,$B$1,$D$1,0) を１つ作成し，C3～G3へコピー･貼り付けすればよい．

	A	B	C	D	E	F	G	H
1	n=	5	p=	0.3
2	X	0	1	2	3	4	5	計
3	P	0.16807	0.36015	0.3087	0.1323	0.02835	0.00243	1.0000

　さいころを投げる場合のように，p が分数の場合
(Excel上では四捨五入した小数として表示するものとして)
B(3, 1/6) の例
　この表を作成するには，D1に =1/6と記入する他は左の例と同様

	A	B	C	D	E	F
1	n=	3	p=	0.1667
2	X	0	1	2	3	計
3	P	0.5787	0.3472	0.0694	0.0046	1.0000

■簡単な穴埋め問題■

(3)
硬貨を400枚投げたとき，表の出る枚数が180枚以上220枚以下となる確率を求めよ．なお，次の正規分布表を利用してよい．

u	1	2	3
p(u)	0.3413	0.4772	0.4987

確率： (※小数第4位まで求めよ)

■Excelを利用する問題■

◇参考◇

左の問題（最大確率の問題）は，筆算でも解くことができる．
p=1/6 として
₅₀C_k+1p^k+1(1-p)^50-k-1 > ₅₀C_kp^k(1-p)^50-k
となるkの範囲を求めると，

これより，･･･<5<6<7<8>9>10>･･･が分かる．　→閉じる←

(*1)引用
○「np≧10 ならばかなり良好といわれている．」･･･「新数学事典」（一松信ほか著;大阪書籍）初版第1版p.664
○「nが，p≦1/2ならばnp>5を，p>1/2ならばnq>5を満たす限り，経験的にこの近似はかなり良好であるといえる．」･･･「初等統計学　原書第4版」（P.G.ホーエル著浅井晃,村上正康訳;培風館p.111）
○「実用的には，np>5かつnq>5ならば，かなりの精度でよく近似されます．」･･･「ゼロから学ぶ統計解析」（小寺平治著;講談社p.92）

確率統計のメニューに戻る

高校数学のメニューに戻る