資料の散布度

→ 携帯版は別頁

== 資料の散布度 ==

この教材で，4.のモーメント，歪度,尖度以外は高校レベルです．

《このページの目次》
※クリックすれば該当項目にジャンプできます

1.　範囲（レンジ）
2.　四分位数，四分位範囲，四分位偏差，5数要約

箱ひげ図，五分位数，十分位数，百分位数

3.　標準偏差，分散

偏差平方和（偏差2乗和もしくは変動），仮平均

4.　変動係数（変異係数）
5.　モーメント，歪度，尖度

正規分布の歪度限界，正規分布の尖度限界，
外れ値の検出

1.　範囲（レンジ）

データの散らばり具合を表す値として，データの最大値から最小値を引いた差をデータの範囲またはレンジという．

【例1】

次のデータは，9人の生徒の右手の握力の測定結果だとします．（単位kg）
　　　36, 35, 36, 38, 42, 52, 32, 45, 48
このデータの最大値はM=52，最小値はm=32だから範囲はM−m=20(kg)です．

範囲はデータの散らばり具合を簡単な引き算によって表すことができますが，極端値（外れ値）に影響されやすいことが弱点です．

【例2】

例1のデータに対して，1人生徒を増やして10人のデータが次のようになった場合
　　36, 35, 36, 38, 42, 52, 32, 45, 48, 72
範囲は72−32=40(kg)になり，1人増えただけで範囲が2倍になってしまいます．

【問題1.1】
次のデータ(A)はある学級の男子の右手の握力，(B)は女子の右手の握力だとします．（単位kg）
(A)　33, 31, 37, 38, 42, 51, 32, 45, 47, 33
(B)　27, 25, 24, 30, 31, 36, 31, 32, 30, 28, 29, 28
この学級の男女右手の握力の散らばり具合をデータの範囲によって判断した場合，男女どちらの散らばり具合が大きいですか.

解答を見る

(A)男子：範囲は51−31=20(kg)
(B)女子：範囲は36−24=12(kg)
　男子の散らばり具合が大きい･･･（答） →閉じる←

2.　四分位数，四分位範囲，四分位偏差，5数要約

2.1　データの散らばり具合を表す値として，データを大きさの順に4分割する3つの数字を四分位数という．四分位数は小さいものから順に第1四分位数（Q1），第2四分位数（Q2），第3四分位数（Q3）という．

2.2　第2四分位数は中央値（メジアン）に等しい．

2.3【四分位数の求め方】
(1)　初めにデータの中央値を求める（これが第2四分位数になる）

上の図のように，データの総数が奇数(n=2k+1)の場合は，第k+1番目の値xk+1が中央値すなわち第2四分位数になる．
データの総数が偶数の場合は，第k番目の値と第k+1番目の値の中央 $\frac{x_k+ x_{k+ 1}}{2}$ を中央値すなわち第2四分位数とする．

(2)　2つに分かれた組の内で小さい方の組の中央値を第1四分位数とする．大きい方の組の中央値を第3四分位数とする．

　(1)の段階でデータの総数が奇数の場合，中央値xk+1は境目の値として大きい方の組にも小さい方の組にも含めない．偶数の場合は，境目が2つの値の中央に来るから，大きい方の個数と小さい方の個数を足せば総数と一致する．
　2つに分かれた組の中で中央値を決める方法は，その組が奇数個であるか偶数個であるかに王寺て(1)のときと同様に行う．

2.4　データの散らばり具合を，四分位数の3個，最大値，最小値の2個の合計5つの数で表す方法を5数要約という．
　5数要約は，株価を表示する箱ひげ図などに使われている．

　ひげを宝物のように大事に考える人たちもいる．
　右図のように，長い「下ひげ」ができたら，その株価は売られ過ぎて反発したことを表し，以後は上昇傾向になることが多い．そこで，長い下ひげができた銘柄を買いの判断材料とし，逆に長い「上ひげ」のできた銘柄を売りの判断材料とする投資家がいると言われている．

　箱ひげ図では，2つ以上の山から成る分布の特徴をうまく表現することはできない．そのような分布は，度数分布表を用いるなど，他の表し方の方がよい．

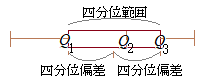
2.5　第3四分位数から第1四分位数を引いた値を四分位範囲という．

　範囲がデータの100%が含まれる区間の大きさを表すのに対して，四分位範囲はデータの中心付近のほぼ50%が含まれる区間の大きさを表す．
　範囲は外れ値の影響を受けやすいが，四分位範囲は外れ値の影響を受けにくい．

　四分位範囲の半分の大きさを四分位偏差という．

　データが中央値の周りに集まっていると，四分位偏差は小さくなる．

2.6　一般の分位数としては，四分位数がよく使われるが，他に次のような分位数も使われている．
•　十分位数 → 厚生労働省賃金構造基本統計調査性,学歴,年齢階級別など
•　五分位数 → 総務省家計調査年間収入など
•　百分位数 → 百分位点(パーセント点)とは，観測データを小さい順に並べたときに，その値よりも小さな値の割合が指定された割合（百分率）になるデータの値．例えば，50パーセント点は中央値と等しく，25パーセント点は第１四分位点に等しい．

【問題1.2】
次のデータの四分位数を求めてください．
　　1, 2, 3, 5, 5, 6, 8, 8, 9

解答を見る

(1) データ総数は9個なので，下から5番目の数5を中央値(=第2四分位数)とする．
(2) 小さい方の組の4個のうちで，2番目と3番目の中央(=2.5)を第1四分位数とする．
　大きい方の組の4個のうちで，小さい方から2番目と3番目の中央(=8)を第3四分位数とする．
Q1=2.5, Q2=5, Q3=8･･･（答） →閉じる←

【問題1.3】
次のデータに対応する箱ひげ図を描いてください．
　　2, 3, 3, 5, 5, 6, 6, 7, 8, 9

解答を見る

(1) データ総数は10個なので，下から5番目と6番目の中央(=5.5)を中央値(=第2四分位数)とする．
(2) 小さい方の組の5個のうちで，3番目(=3)を第1四分位数とする．
　大きい方の組の5個のうちで，小さい方から3番目(=7)を第3四分位数とする．
(3) 最小値は2, 最大値は9

･･･（答） →閉じる←

【問題1.4】

	数学	英語
最小値	10	20
第1四分位数	25	40
第2四分位数	40	60
平均値	45	55
第3四分位数	65	70
最大値	90	80

　右の表は，ある学級の数学と英語の得点を集計したものだとします．
(1)　数学,英語の得点の範囲，四分位範囲を求めてください．
(2)　得点の散らばりが大きいのはどの教科ですか．

解答を見る

(1)　数学：範囲 90−10=80, 四分位範囲 65−25=40
　　英語：範囲 80−20=60, 四分位範囲 70−40=30
　四分位範囲の比較により，数学の方が散らばりが大きいと言える･･･（答） →閉じる←

【問題1.5】

　右図の度数分布表①②③に対応する箱ひげ図を，下の(A)(B)(C)から選んでください．

解答を見る

②は左右対称に近いから(A)
①は中央値が右寄りだから(B)
③は中央値が左寄りだから(C) →閉じる←

【問題1.6】

　右のグラフは，標準正規分布
$\phi(z)=\frac{e^{-\frac{x^2}{2}}}{\sqrt{2\pi}$
の累積相対度数分布を表わしたものです．
　このグラフから言える，95パーセント点として最も近い値を，下の選択肢から選んでください．
① z=1.96,　②z=1.66,　③z=2.50,　④z=−1.50

解答を見る

F(z)=0.95となるzの値を読み取ります．
　　② z=1.66･･･（答） →閉じる←

3.　標準偏差，分散

3.1　データの散らばり具合を表す値として，各観測値xkから平均値μを引いたものxk−μを偏差という．

平均値からのズレの量を調べるのは，よい考えであるが，平均値よりも大きいものと平均値よりも小さいものがあって，偏差を全部加えると0（零）になって消えてしまうところが難点である．
$\mu=\frac{1}{n}\sum_{k=1}^nx_k=\frac{x_1+ x_2+\cdots x_n}{n}$
だから
$\sum_k^n(x_k-\mu)=n\mu-n\mu=0$

　上記のように偏差は，総和が零になって使いにくいので，その弱点を取り除くために，偏差に絶対値を付けた平均偏差|xk−μ|がある．

　絶対値が付いているので，平均値よりも大きな観測値xkに対しても，小さな観測値に対しても，平均値からのズレを正の値で表すことができ，観測値と同じ単位で表せるのがよい点であるが，「絶対値記号は変形しにくい」（通常使う展開公式などが使えないなど）難点があり，あまり利用されない．

　上記の偏差や平均偏差の弱点を克服できるものとして，次の分散，標準偏差が最もよく利用されている．実際，統計において散らばり具合を表す量として，ほとんどの場合に分散，標準偏差が用いられている．
分散
$V=\frac{1}{n}\sum_{k=1}^n(x_k-\mu)^2$
標準偏差
$s=\sqrt{V}=\sqrt{\frac{1}{n}\sum_{k=1}^n(x_k-\mu)^2}$

　分散は，偏差を２乗しているので，元の観測値xkと単位が一致しないが，多項式の2乗として展開・整理など変形しやすいよさがある．分散にルートを使た標準偏差にすれば，元の観測値xkと単位が一致する．

　偏差平方和（偏差2乗和もしくは変動）とは，次の式のことを言う．

$S=\sum_{k=1}^n(x_k-\mu)^2$ あるいは $S=\sum_{k=1}^n(x_k-\bar{x})^2$

　データの散らばりを調べるとき，分散と標準偏差が最もよく利用されるが，偏差平方和はそれらの途中計算に登場する．
　２つのデータを合併したとき，平均や分散は加算的ではない（平均の和や分散の和が合併したデータの平均や分散にはならない）が，総和や偏差平方和は加算的である（単純に足せばよい）．

《重要公式》

【平均値の定義】
$\mu=\bar{x}=\frac{x_1+ x_2+\cdots+ x_N}{N}=\frac{1}{N}\bigl(\sum_{k=1}^N x_k\bigr)$ ･･･(1.1)
【分散の定義】
$V(x)=\frac{1}{N}\sum_{k=1}^N(x_k-\mu)^2$
$=\frac{1}{N}\sum_{k=1}^N(x_k-\bar{x})^2$ ･･･(1.2)
【標準偏差の定義】
$\sigma=\sqrt{V(x)}=\sqrt{\frac{1}{N}\sum_{k=1}^N(x_k-\mu)^2}$
$=\sqrt{\frac{1}{N}\sum_{k=1}^N(x_k-\bar{x})^2}$ ･･･(1.3)
【分散の式の変形】
$V(x)=\frac{1}{N}\sum_{k=1}^Nx_k^2-\mu^2$
$=\frac{1}{N}\sum_{k=1}^Nx_k^2-\bar{x}^2$ ･･･(1.4)
【標準偏差の式の変形】
$\sigma=\sqrt{\frac{1}{N}\sum_{k=1}^Nx_k^2-\mu^2}$
$=\sqrt{\frac{1}{N}\sum_{k=1}^Nx_k^2-\bar{x}^2}$ ･･･(1.5)
※分散および標準偏差で，分母をN−1とするよく似た式が登場することがあるが，このページの大部分･･･(7.1)(7.2)(9.1)(9.2)以外･･･で述べているのは，記述統計として母集団のデータ自体を扱っている場合の公式です．
　これに対して，分母をN−1とするのは，母集団から抽出されたN個の標本から母集団の分散，標準偏差の値を推定するときに使う推測統計の公式です．

【度数分布表から求まる平均値】
$\mu=\bar{x}=\frac{x_1f_1+ x_2f_2+\cdots+ x_nf_n}{N}$
$=\frac{1}{N}\bigl(\sum_{k=1}^n x_kf_k\bigr)$ ･･･(2.1)
　　（ただし， $f_1+ f_2+\cdots+ f_n=N$ ）
【度数分布表から求まる分散】
$V(x)=\frac{1}{N}\sum_{k=1}^n(x_k-\mu)^2f_k$
$=\frac{1}{N}\sum_{k=1}^n(x_k-\bar{x})^2f_k$ ･･･(2.2)
【度数分布表から求まる標準偏差】
$\sigma=\sqrt{V(x)}=\sqrt{\frac{1}{N}\sum_{k=1}^n(x_k-\mu)^2f_k}$
$=\sqrt{\frac{1}{N}\sum_{k=1}^n(x_k-\bar{x})^2f_k}$ ･･･(2.3)
【分散の式の変形】
$V(x)=\frac{1}{N}\sum_{k=1}^nx_k^2f_k-\mu^2$
$=\frac{1}{N}\sum_{k=1}^nx_k^2f_k-\bar{x}^2$ ･･･(2.4)

$f_1+ f_2+\cdots+ f_n=N$
階級幅は $c$
$u=\frac{x-x_0}{c}\hspace{5}\leftrightarrow\hspace{5}x=x_0+ cu$
とするとき

【度数分布表で仮平均から求まる平均値】
$\mu=\bar{x}=x_0+ c\bar{u}$ ･･･(3.1)
【度数分布表で仮平均から求まる分散】
$V(x)=c^2V(u)$ ･･･(3.2)
【度数分布表で仮平均から求まる標準偏差】
$\sigma_x=c\sigma_u$ ･･･(3.3)

《重要公式の解説》
(1.1)，(1.2)，(1.3)←
　これらが平均値，分散，標準偏差の定義です．
Excel関数で直接計算できるのは，これらの
$x_1,\hspace{2}x_2,\hspace{2}\cdots\hspace{2},\hspace{2}x_n$
の形でデータが与えられる場合です．後に登場する度数分布表で与えられた場合については，直接に平均，分散，標準偏差を値を求める関数は用意されていません．
①データの個数, ②データの総和, ③平均値, ④分散, ⑤標準偏差

①=count(), ②=sum(), ③=average(), ④=varp(), ⑤=stdevp()
※これらのExcel関数の中身が(1.1)～(1.3)式になっています．
※var()やstdev()は推測統計で母集団の不偏分散，不偏標準偏差を求めるものです．[このページで扱っている記述統計の基本とは少しだけ違います]

(1.4)，(1.5)←
(1.2)を変形すると
$V(x)=\frac{1}{N}\sum_{k=1}^N(x_k-\mu)^2$
$=\frac{1}{N}\{\sum_{k=1}^N(x_k^2-2\mu x_k+ \mu^2)\}$
$=\frac{1}{N}\{\sum_{k=1}^N x_k^2-2\mu\sum_{k=1}^N x_k+ \sum_{k=1}^N\mu^2\}$

(1.1)により
$\sum_{k=1}^N x_k=N\mu$ だから
$V(x)=\frac{1}{N}\{\sum_{k=1}^Nx_k^2-2\mu\cdot N\mu+ N\mu^2\}$
$=\frac{1}{N}\{\sum_{k=1}^Nx_k^2-N\mu^2\}$
$=\frac{1}{N}\sum_{k=1}^Nx_k^2-\mu^2$ ･･･(1.4)■証明終わり■
なお，2乗平均 $\frac{1}{N}\sum_{k=1}^Nx_k^2$ は $\bar{x^2}$ とも書かれ，平均 $\mu$ は
$\bar{x}$ と書くことができるから
$V(x)=\bar{x^2}-(\bar{x})^2$ と書くことができる．

(1.4)のルートが(1.5)となる．

◎簡単な例で公式の使い形を身に着けよう！

【問題2.1】

観測値	偏差	偏差平方
xk	xk−μ	(xk−μ)2
1	−3	9
3	−1	1
4	0	0
5	1	1
7	3	9
偏差平方和		ア

　右の表で与えられるデータについて，分散と標準偏差を求めたい．
　はじめに，観測値の個数が5個で観測値の総和が20であることから，平均値μ=4が求まる．
　次に，この平均値μを使って，偏差，偏差平方の表を埋めて行くと，偏差平方和はアになる．これにより，分散イ，標準偏差ウが求まる．
　空欄のアイウを埋めてください．

解答を見る

偏差平方を縦に足すと
偏差平方は，20
分散は， $V(x)=\frac{20}{5}=4.0$
標準偏差は， $\sigma=\sqrt{V(x)}=2.0$
→閉じる←

度数分布表から分散，標準偏差を求める

【問題2.2】

階級	階級値	度数		偏差	偏差平方
以上.未満	xk	fk	xkfk	xk−μ	(xk−μ)2	(xk−μ)2fk
0≦x1<10	5	1	5	−19	361	361
10≦x2<20	15	2	30	−9	81	162
20≦x3<30	25	4	100	1	1	4
30≦x4<40	35	3	105	11	121	363
40≦x5<50	45	0	0	21	441	0
	個数	10
	総和平均		240 24.0		偏差平方和	890

　上の度数分布表で与えられるデータについて，分散と標準偏差を求めたい．
　はじめに，度数の合計が10でxkfkの総和が240であることから，平均値μ=24が求まる．
　次に，この平均値μを使って，偏差，偏差平方，偏差平方和×度数の表を埋めて行くと，偏差平方和×度数の和は890になる．これにより，分散ア，標準偏差イが求まる．
　空欄のアイを埋めてください．

解答を見る

分散は， $V(x)=\frac{890}{10}=89.0$
標準偏差は， $\sigma=\sqrt{V(x)}=9.43$
→閉じる←

※このような度数分布表で与えられたデータの平均値，分散，標準偏差をExcelのワークシート関数で直接計算することはできません．上記のようなデータの場合，階級値に度数分のデータがあるものとして
　　　5, 15, 15, 25, 25, 25, 25, 35, 35, 35
というデータについて，=average(), =varp, =stdevp()などの関数を使うとできます．

(分散)＝(2乗平均)－(平均)²の公式を使う

【問題2.3】

階級値	度数
xk	fk	xkfk	xk2	xk2fk
5	2	10
15	5	75
25	6	150
35	5	175
45	2	90
和	20	500		ア
平均	25			イ

　右の度数分布表で与えられるデータについて，平均値μ=25，分散σ²=130であるとき
　　階級値²×度数の和：ア
　　2乗平均：イ
は幾らになりますか．

解答を見る

xk2，xk2fkを順に埋めて行けば求められるが，ここでは分散の値が書かれているから，逆算により次の答案が書ける．
　　(分散)＝(2乗平均)－(平均)²の公式により
　　130=(2乗平均)−25²
　　(2乗平均)=130+625=755→イ
　　イ²×20=15100→ア
→閉じる←

仮平均を用いた計算

【問題2.4】

xk	fk
5	1
15	2
25	3
35	3
45	1

　右の表のように階級値xk，度数fkが与えられている変数について，仮平均を使って，平均値，分散，標準偏差を求めてください．

解答を見る

xk	fk	uk	ukfk	uk2	uk2fk
5	1	−2	−2	4	4
15	2	−1	−2	1	2
25	3	0	0	0	0
35	3	1	3	1	3
45	1	2	2	4	4

　右の表のように，x0=25, c=10として仮平均
$u=\frac{x-x_0}{c}$
を導入すると
$\bar{u}=\frac{-2-2+ 0+ 3+ 2}{10}=\frac{1}{10}=0.1$
$\bar{x}=x_0+ c\bar{u}=25+ 10\times 0.1=26$ ･･･（答）
$V(c)=\bar{u^2}-\bar{u}^2=\frac{13}{10}-0.1^2=1.29$
$V(x)=c^2V(c)=129$ ･･･（答）
$\sigma=\sqrt{129}=11.36$ ･･･（答）

→閉じる←

4.　変動係数（変異係数）

　平均値が異なる2つの量や身長と体重のように単位の異なる2つの量の散らばり具合を比較するとき，単純に標準偏差の大きさだけで比較すると判断を誤る．
　このような場合には，(標準偏差)÷(平均値)で定義される変動係数（変異係数）によって比較するのがよい．（同一単位の量の比で定義される変動係数は，単位を持たない数値で，CV［Coefficient of Variation：この直訳が変動係数］で表される．）
　変動係数はパーセントで表される場合もある．

【例】
(1) 幼稚園児と成人の身長の散らばり具合を比較する場合，身長の平均値が全く異なるため，標準偏差を単純に比較しても散らばり具合の比較として適当ではない．このような場合には，(標準偏差)÷(平均値)で定義される変動係数によって比較するのがよい．

(2) 中学3年生の身長と体重の散らばり具合を比較する場合，単位も数値の大きさも全く異なるため，標準偏差を単純に比較しても散らばり具合の比較として適当ではない．このような場合には，(標準偏差)÷(平均値)で定義される変動係数によって比較するのがよい．

※文部科学省や厚生労働省の多くの統計資料で，平均値，標準偏差と並んで変動係数も示されている．

※筆者が困ったなと思う問題の備忘録
　変動係数は，(標準偏差)÷(平均値)で定義され，割り算が可能な変数であることを前提としている．したがって，変動係数を定義できるのは比例尺度の変数に限られる．
　ところが，統計の教科書で，英語・国語・数学などで満点を100点として行われる試験の得点は間隔尺度であって，比例尺度ではないとされている．
　以上の２つの事柄を前提とすると

ⅰ）英語・国語・数学などの試験の得点は，変動係数を使って比較することはできないはずである．

ⅱ）比例尺度でない試験の得点に対して，平均値の半分というような基準は意味を持たないはずである．

ⅰ）数学と英語の得点について，変動係数を使って散らばり具合を比較するという問題は，普通に見かけるが，得点は理屈上間隔尺度であるはずだからつじつまが合わないように思う．

ⅱ）高校では近年，到達度を基にした絶対的評価になったが，戦後長い間にわたって平均点を基準とする相対的絶対評価が行われてきた．すなわち，小中学校では正規分布を前提とする相対評価によって，5,4,3,2,1の人数比が固定されていたのに対して，高校では単位認定・進級認定を行う都合もあって，相対評価は行われず，また戦前の旧制高校のような認定主義による絶対評価も行われなかった．（少なくとも実技教科以外では）

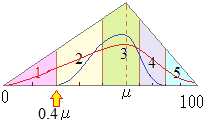　平均点を基にした相対的絶対評価を図で示すと，右図のようになる．（このようなグラフは，どこにも書いてない･･･いわゆる換算表というものを，筆者が見やすい形に直したもの．）これに当てはめて，クラス平均の40%もしくは半分以下の者を成績不振による単位不認定とする．
　（正規分布を前提とする相対評価との端的な違いは，評価1とか5の人数比は固定されておらず，標準偏差が小さい場合，単位不認定となる評価1はめったに生じない（青い曲線の場合）．逆に，標準偏差の大きなクラス［できる者とできない者が一緒に学んでいるクラス］では，評価1，5が出やすい（赤い曲線の場合））
　ところで，比例尺度でない試験の得点に対して，平均値の半分というような基準は意味を持たないはずであるから，戦後約60年間行われて来た高校の単位認定基準の原理的な根拠は，本当に大丈夫だったのか？理論的には相対評価と絶対評価の折衷主義であるが，経験的には抜群の安定感がある経験則として使われており，得点は比例尺度として和差積商の変換が当然のように行える．零点には絶対的な意味があり，教えられた内容のうちで習得できたものが０%だったという意味になる．

【問題3.1】

男子体重	平均	標準偏差
小学1年	21.6	3.55
中学3年	55.3	10.62

女子体重	平均	標準偏差
小学1年	21.1	3.42
中学3年	50.8	8.09

　上の表は，ある年の小学校1年生と中学校3年生の男女別体重の平均と標準偏差です．男女，小1中3の4通りの組合せのうちで，変動係数が最も大きいものはどれですか．

解答を見る

男子体重	平均	標準偏差	変動係数
小学1年	21.6	3.55	0.164
中学3年	55.3	10.62	0.192

右の表により，変動係数は,
小1男子 0.164
中3男子 0.192

女子体重	平均	標準偏差	変動係数
小学1年	21.1	3.42	0.162
中学3年	50.8	8.09	0.159

右の表により，変動係数は,
小1女子 0.162
中3女子 0.159
　中3男子の変動係数が最も大きい･･･（答） →閉じる←

この教材の4.モーメント，歪度,尖度は大学レベルです．

5.　モーメント，歪度，尖度

【以下の内容のざっくりとした要約】
(1)　観測値xkの１次式 ⇒ 平均値（中心付近の場所）
(2)　観測値xkの２次式 ⇒ 分散（散らばり具合）
(3)　観測値xkの３次式 ⇒ 歪度（左右の片寄り）
(4)　観測値xkの４次式 ⇒ 尖度（中心部分の尖り具合，すそ野の広がり具合）

　原点のまわりのモーメント（積率）は
$m_1=\frac{1}{N}\sum_{k=1}^Nx_k$ ･･･(1.1)
で定義される。度数分布表で与えられるデータに対しては
$m_1=\frac{1}{N}\sum_{k=1}^nx_kf_k$ ･･･(1.2)

(1.2)は，始点（原点）からの距離がx1である点に重さf1の重りが，･･･x1である点に重さfnの重りがあるときの（原点のまわりの回転の）力のモーメントとして，てこの原理で習うものです．

　一般に，p次のモーメントは
$m_p=\frac{1}{N}\sum_{k=1}^Nx_k^p$ ･･･(2.1)
$m_p=\frac{1}{N}\sum_{k=1}^nx_k^pf_k$ ･･･(2.2)
で定義されます．

　特に，１次のモーメントは，平均値（期待値）に対応します．
$m_1=\mu=\frac{1}{N}\sum_{k=1}^Nx_k$ ･･･(1.1')
$m_1=\mu=\frac{1}{N}\sum_{k=1}^nx_kf_k$ ･･･(1.2')

　点aのまわりのモーメントは
$m_p=\frac{1}{N}\sum_{k=1}^N(x_k-a)^p$ ･･･(3.1)
$m_p=\frac{1}{N}\sum_{k=1}^n(x_k-a)^pf_k$ ･･･(3.2)
で定義され，特にaとして平均値μを選んだものをp次の中心モーメントという．
$\mu_p=\frac{1}{N}\sum_{k=1}^N(x_k-\mu)^p$ ･･･(4.1)
$\mu_p=\frac{1}{N}\sum_{k=1}^n(x_k-\mu)^pf_k$ ･･･(4.2)

※１次の中心モーメントは，”偏差の平均”になるから，0です．
$\mu_1=\frac{1}{n}\sum_{k=1}^N(x_k-\mu)$
$=\frac{1}{N}\sum_{k=1}^Nx_k-\frac{1}{N}\times N\times\mu$
$=\mu-\mu=0$

　２次の中心モーメントは，分散に対応します．
$\mu_2=\frac{1}{N}\sum_{k=1}^N(x_k-\mu)^2=\sigma^2$ ･･･(5.1)
$\mu_2=\frac{1}{N}\sum_{k=1}^n(x_k-\mu)^2f_k=\sigma^2$ ･･･(5.2)

　３次の中心モーメントをそのまま書けば，次の式になる．
$\mu_3=\frac{1}{N}\sum_{k=1}^N(x_k-\mu)^3$
$\mu_3=\frac{1}{N}\sum_{k=1}^n(x_k-\mu)^3f_k$
　この式は，平均値μと標準偏差σの影響を受けて変化するが，次のように変数の標準化を行うと，平均値μと標準偏差σの影響を受けず，いずれも平均値0，標準偏差1の分布になる．
$\bigl(Z=\frac{X-\mu}{\sigma}\bigr)$

■記述統計の場合■
《与えられたデータ自体を母集団と見なす場合》
　変数を標準化して求められる３次の中心モーメントは，歪度と呼ばれ，非対称性の度合いを表す．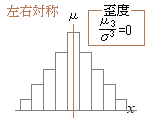
$g_1=\frac{\mu_3}{\sigma^3}=\frac{1}{N}\sum_{k=1}^N(\frac{x_k-\mu}{\sigma})^3$ ･･･(6.1)
$g_1=\frac{\mu_3}{\sigma^3}=\frac{1}{N}\sum_{k=1}^n(\frac{x_k-\mu}{\sigma})^3f_k$ ･･･(6.2)

ア）　左右対称な分布であるとき，３次関数は奇関数だから，右半分が正の符号になる分と左半分で負の符号になる分が打ち消しあって消えるから，歪度は0になる．

イ）　左の裾すそが長い（左に長いテールがある，単峰が右寄りになっている）とき，左側の３乗が強く働くから，歪度は負になる．

ウ）　右の裾すそが長い（右に長いテールがある，単峰が左寄りになっている）とき，右側の３乗が強く働くから，歪度は正になる．
【例】

-- 図1 --　　　　　　　　-- 図2 --

■推測統計の場合■
《与えられたデータを標本として母集団の値を推定する場合》
$g_1=\frac{\mu_3}{\sigma^3}=\frac{N}{(N-1)(N-2)}\sum_{k=1}^N(\frac{x_k-\mu}{\sigma})^3$ ･･･(7.1)
$g_1=\frac{\mu_3}{\sigma^3}=\frac{N}{(N-1)(N-2)}\sum_{k=1}^n(\frac{x_k-\mu}{\sigma})^3f_k$ ･･･(7.2)

Excelのワークシート関数skew()は，上記(7.1)の推測統計の値になります．[skewness:歪度]
Excelで［データ］→［データ分析］→［基本統計量］と進むと，歪度や尖度の値が出力されます．

《およその目安》
　歪度は左右対称性を数値化したものです．歪度が0に近い分布は，左右対称であると言えます．
• |歪度|<0.5のときは，ほぼ対称です．
• 0.5≦|歪度|<1のときは，少し歪ゆがんでいます．
• |歪度|≧1のときは，かなり歪ゆがんでいます．

　あるデータがどのような分布になるかは，度数分布表によって視覚的に分かることが多い．例えば，中心部の位置，散らばり具合，左右の片寄りなど，度数分布表によって分かることは多い．
　しかし，例えば誤差を除けば正規分布と見なせるかどうか，指数分布，一様分布など他の分布に由来するものでないかどうかは，歪度の数値を使った検定によって判断することができる．
　歪度，尖度もしくはそれら両方を使って正規性の検定を行う方法が考えられている．次のような限界の値を見て，歪度|b1|の値からその分布が正規分布と見なせせるかどうかを判断します．（この表よりも大きければ正規分布でないとする）
$u\times\sqrt{\frac{6N(N-1)}{(N-2)(N+ 1)(N+ 3)}}$ フィッシャーによる
5%:u=1.96, 　1%:u=2.58

-表1- (正規分布の歪度限界)
N	10	11	12	13	14	15	16	17	18	19
5%	1.347	1.295	1.249	1.208	1.171	1.137	1.106	1.078	1.051	1.027
1%	1.773	1.705	1.644	1.590	1.541	1.497	1.456	1.418	1.384	1.351

N	20	21	22	23	24	25	26	27	28	29
5%	1.004	0.982	0.962	0.943	0.926	0.909	0.893	0.878	0.863	0.850
1%	1.321	1.293	1.267	1.242	1.218	1.196	1.175	1.155	1.137	1.119

N	30	40	50	60	70	80	90	100	200	300
5%	0.837	0.733	0.660	0.605	0.562	0.527	0.498	0.473	0.337	0.276
1%	1.101	0.964	0.868	0.796	0.740	0.694	0.655	0.623	0.444	0.363

　４次の中心モーメントをそのまま書けば，次の式になる．
$\mu_4=\frac{1}{N}\sum_{k=1}^N(x_k-\mu)^4$
$\mu_4=\frac{1}{N}\sum_{k=1}^n(x_k-\mu)^4f_k$
　この式は，平均値μと標準偏差σの影響を受けて変化するが，次のように変数の標準化を行うと，平均値μと標準偏差σの影響を受けず，いずれも平均値0，標準偏差1の分布になる．
$\bigl(Z=\frac{X-\mu}{\sigma}\bigr)$

■記述統計の場合■
《与えられたデータ自体を母集団と見なす場合》
　変数を標準化して求められる３次の中心モーメントは，尖度と呼ばれ，中心部分の尖り具合，すそ野の広がり具合を表す．
$g_2=\frac{\mu_4}{\sigma^4}=\frac{1}{N}\sum_{k=1}^N(\frac{x_k-\mu}{\sigma})^4$ ･･･(8.1)
$g_2=\frac{\mu_4}{\sigma^4}=\frac{1}{N}\sum_{k=1}^n(\frac{x_k-\mu}{\sigma})^4f_k$ ･･･(8.2)

ただし，正規分布の尖度が3になり，正規分布との比較の都合上，尖度の中心を3とする定義がよく用いられる．
$g_2=\frac{\mu_4}{\sigma^4}-3=\frac{1}{N}\sum_{k=1}^N(\frac{x_k-\mu}{\sigma})^4-3$ ･･･(8.1’)
$g_2=\frac{\mu_4}{\sigma^4}-3=\frac{1}{N}\sum_{k=1}^n(\frac{x_k-\mu}{\sigma})^4f_k-3$ ･･･(8.2’)

■推測統計の場合■
《与えられたデータを標本として母集団の値を推定する場合》
$g_2=\frac{N(N+ 1)}{(N-1)(N-2)(N-3)}\sum_{k=1}^N(\frac{x_k-\mu}{\sigma})^4-\frac{3(N-1)^2}{(N-2)(N-3)}$

･･･(9.1)

$g_2=\frac{N(N+ 1)}{(N-1)(N-2)(N-3)}\sum_{k=1}^n(\frac{x_k-\mu}{\sigma})^4f_k-\frac{3(N-1)^2}{(N-2)(N-3)}$

･･･(9.2)

　Excelのワークシート関数kurt()は，上記(9.1)の推測統計の値になります．[kurtosis:尖度]
　Excelで［データ］→［データ分析］→［基本統計量］と進むと，歪度や尖度の値が出力されます．
　(9.1)(9.2)の定義で，

• 正規分布の尖度は0になり，
• 尖度が正の分布は，中央部分が正規分布よりも尖っていて，
• 尖度が負の分布は，すそ野の広い平坦なものになる

というのが原則ですが，双峰型，一様分布など様々な分布があり，必ずしも原則通りとは限りません．
　様々な統計で，平均値や標準偏差だけで分布の様子を判断されることが多いが，投資などの分野においては，歪度，尖度なども用いてテールリスクの回避が図られると言われている．例えば，尖度が大きいと，中心部分が尖っているだけでなく，すそ野も広がるので，テールリスクがあるなど.
　次のような限界の値を見て，尖度|b2|の値からその分布が正規分布と見なせせるかどうかを判断します．（この表よりも大きければ正規分布でないとする）
$u\times\sqrt{\frac{24N(N-1)^2}{(N-3)(N-2)(n+ 3)(n+ 5)}}$ フィッシャーによる
5%:u=1.96, 　1%:u=2.58

-表2- (正規分布の尖度限界)
N	10	11	12	13	14	15	16	17	18	19
5%	2.615	2.508	2.415	2.334	2.262	2.197	2.138	2.084	2.034	1.988
1%	3.442	3.301	3.179	3.072	2.977	2.892	2.814	2.743	2.678	2.617

N	20	21	22	23	24	25	26	27	28	29
5%	1.945	1.905	1.867	1.832	1.799	1.767	1.738	1.709	1.682	1.657
1%	2.560	2.508	2.458	2.412	2.368	2.326	2.287	2.250	2.214	2.181

N	30	40	50	60	70	80	90	100	200	300
5%	1.632	1.436	1.297	1.193	1.110	1.042	0.986	0.938	0.671	0.550
1%	2.148	1.890	1.708	1.570	1.461	1.372	1.298	1.234	0.883	0.724

(1)　尖度という用語の意味は「尖りとがり具合」ということで，中心部分が尖っていれば尖度は大きくなり，全体として平坦な分布であれば尖度が小さな値になるというのが第1の解釈です．
(2)　尖度の使い方として，この他に「外れ値はずれ」の検出があります．これは， $(\frac{x_k-\mu}{\sigma})^4$ という式の形に関係しており，左右いずれの方向に対しても平均値から外れた値があると，それを4乗すると大きな値になり，尖度が大きくなる傾向があります．

(その1)
　外れ値の存在は，度数分布表を見れば見当がつきますが，ではどの程度外れていれば「外れ値」と見なすのかということについて，よく使われる１つの目安として，箱ひげ図で
　　第3四分位数+1.5×四分位範囲より大きい値
　　第1四分位数−1.5×四分位範囲より小さい値
は外れ値と判断する．
(その2)
　尖度が5以上ならば外れ値が含まれる可能性が高い，尖度が10以上ならばほ確実に外れ値があると判断する．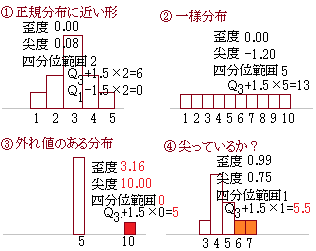

《歪度，尖度の正規性検定，外れ値の検出:具体例》

-- 図3 --

①は，歪度0.00（左右対称）で表1のN=10の場合の表から，5%の有意差はないから正規分布という帰無仮説は棄却されない.尖度0.08で正規分布よりはわずかに尖っているが，表2のN=10の場合の表から，5%の有意差はないから正規分布という帰無仮説は棄却されない.
外れ値の有無：四分位範囲×1.5で調べる外れ値なし，尖度5または10以上に該当しない

②は，一様分布で，歪度0.00（左右対称）で表1のN=10の場合の表から，5%の有意差はないから正規分布という帰無仮説は棄却されない.尖度−1.20で正規分布と比べて（見ただけで分かる）ずいぶんと平坦な分布になっている（ただし，一様分布で尖度が−1.2程度だということは参考になる．このことはデータ数が20,30となっても変わらず，一様分布の尖度は−1.20になるようである）．表2のN=10の場合の表から，5%の有意差はないから正規分布という帰無仮説は棄却されない.
外れ値の有無：四分位範囲×1.5で調べる外れ値なし，尖度5または10以上に該当しない

③は，歪度3.16で右に大きくゆがんでいる.表1のN=10の場合の表から，5%の有意差を超えるから，正規分布という帰無仮説は棄却される.尖度10.00で表2のN=10の場合の表から，5%の有意差を超えるから，正規分布という帰無仮説は棄却される.
外れ値の有無：観測値10は四分位範囲×1.5で調べる外れ値に該当する．尖度10は外れ値の存在を示している．

④は，尖っていると見なせるかどうかの参考として調べたもの．歪度0.99で正だからやや山は左，テールは右と言える．表1のN=10の場合の表から，5%の有意差はないから正規分布という帰無仮説は棄却されない.尖度0.75で正規分布よりはわずかに尖っているが，表2のN=10の場合の表から，5%の有意差はないから正規分布という帰無仮説は棄却されない.
外れ値の有無：観測値6,7は四分位範囲×1.5で調べる外れ値に該当する．尖度0.75は外れ値は外れ値を検出しない．（この例では四分位範囲によるはいずれ値の検出と尖度による外れ値の検出は一致しない．データ数がもっと多ければ，外れ値なしと判断する事例だと思われる）

【問題4.1】 0.1, 2.1, 2.6, 2.7, 3.4, 3.6, 4.1, 4.6, 4.8, 5.0,
5.0, 5.1, 5.1, 5.2, 5.2, 5.2, 5.3, 5.3, 5.4, 9.9 　上の20件のデータの統計量を求めると，平均値4.5, 不偏分散3.59, 歪度0.43, 尖度3.69，第1四分位数3.5, 中央値5.0, 第3四分位数5.2になっています．
(1)　このデータを有意水準5%で正規分布と見なせるかどうか，表1，表2の両方について限界内にあるか否かで判断してください．
(2)　このデータに外れ値があるどうか，四分位範囲×1.5倍の基準，尖度が5以上の各々の基準で判断してください．

解答を見る

　大きさ20のデータで歪度0.43<1.004は表1の限界内にある．大きさ20のデータで尖度3.69>1.945は表2の限界を超えているから，正規分布であるという帰無仮説は棄却される．
　四分位範囲は5.2−3.5=1.7で，第3四分位数+1.5×四分位範囲=7.75<9.9だから，観測値9.9は四分位範囲の基準で外れ値と見なせる．尖度3.69<5だから尖度の基準では外れ値があるとは言えない． →閉じる←

【問題4.2】
0.1, 0.7, 1.4, 1.8, 2.1, 2.1, 3.7, 3.8, 3.8, 3.8,
3.9, 4.4, 4.6, 5.9, 6.6, 6.6, 6.7, 6.8, 7.1, 7.5 　上の20件のデータの統計量を求めると，平均値4.2, 不偏分散5.22, 歪度−1.15, 尖度−1.12，第1四分位数2.1, 中央値3.85, 第3四分位数6.6になっています．
(1)　このデータを有意水準5%で正規分布と見なせるかどうか，表1，表2の両方について限界内にあるか否かで判断してください．
(2)　このデータに外れ値があるどうか，四分位範囲×1.5倍の基準，尖度が5以上の各々の基準で判断してください．

解答を見る

　大きさ20のデータで|歪度|=1.15>1.004は表1の限界を超えている（平坦過ぎる）から，正規分布であるという帰無仮説は棄却される．（|尖度|=1.1<1.945の方は，表2の限界内にある．）
　四分位範囲は6.6−2.1=4.5で，第3四分位数+1.5×四分位範囲=13.35>7.5だから，上側の外れ値はない．第1四分位数−1.5×四分位範囲=−4.65<0.1だから，下側の外れ値もない．尖度−1.15<5だから尖度の基準で外れ値はない． →閉じる←

確率統計のメニューに戻る

高校数学のメニューに戻る