■ 度数分布表,相対度数分布表■例1■右のデータは,1学級40人分についてのある試験(100点満点)の得点であるとする.(数えやすくするために小さい順に並べてある.)このデータについて,度数分布表とヒストグラムを作りたい. |
0, 2, 15, 15, 18, 19, 24, 26, 27, 32, 32, 33, 40, 40, 44, 44, 45, 49, 52, 54, 55, 55, 59, 61, 64, 64, 67, 69, 70, 71, 71, 77, 80, 82, 84, 84, 85, 86, 91, 100 |
||||||||||||||||||||
|
【チェックポイント】 ○ 階級の個数は少な過ぎても,多過ぎてもよくない. (グラフで考えてみる.)○ 階級の個数は,最大値と最小値の間を,5〜20個とか,10〜15個程度に分けるのが目安とされている.(書物によって示されている目安は異なるが,あくまで目安として記憶にとどめる.) 階級の個数の目安として,スタージェスの公式(※) ○ 階級の幅は等間隔にとるのが普通. ○ 身長や体重のように連続的な値をとるデータを階級に分けるときは,ちょうど階級の境目となるデータが登場する場合があるので,0≦x1<10,10≦x2<20,・・・ のように境目のデータをどちらに入れるかをあらかじめ決めておく. ○ ヒストグラム (・・・グラフではない) 度数分布を柱状のグラフで表わしたもの. |
図1
  ※ スタージェス:人名 この公式で階級の個数を求めたときの例
例えば約50万人が受けるセンター試験の得点分布を考えると,この公式では 1 + log2500000 = 約20となるが,実際の資料では1点刻み(101階級)でも十分なめらかな分布となる.要するに,「目安」は参考程度と考える. |
| 例1の案 | |||||||||||||||
度数分布表
|
ヒストグラム
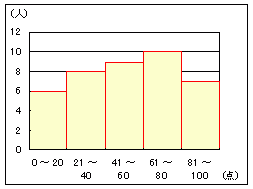 |
||||||||||||||
| 参考 | |||||||||||||||
| 1 スタージェスの公式で計算すれば,N=40のとき階級の個数nの「目安」は約6〜7であるが,95-1=94(得点は95種類)や100点を6〜7個に分割すると,16点〜14点間隔の階級となり,この分析を読む人はそのような不自然な分割は好まず,10点ないし20点刻みのグラフに慣れていると考えられる. 10点ないし20点刻みにすると,度数分布表から平均値や標準偏差を計算するときに,階級の中央値がすっきりした値になる利点がある. 10点という分け方を検討してみると,次のグラフのように凹凸がひどくて規則性がきれいにならないので,結果を見てからやめる. 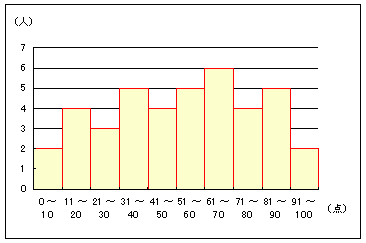 |
2 身長や体重のような連続量の場合は等分できるが,この問題のように整数値だけをとるときは,各階級の区間が等しくならないことがある:1点から100点で値は100種類であるが,0点があるので得点は101種類.左の例では0〜20の階級が一個分多くなっている. 3 ヒストグラムは,いわゆる棒グラフと違って縦棒の間に隙間を作らない. すなわち,あるグループにおける血液型別人数表,出身都道府県別人数表のように定性的な分類(カテゴリーデータ)を棒グラフにするときは,下の図のように棒の間に隙間のあるグラフとする.これに対して,本来つながっている数値の区間を集計の都合で適当に分けてできるヒストグラムでは,隙間のない棒グラフを使う. (Excelで棒グラフを作成したとき,隙間のないグラフにするには,棒を右クリック→データ系列の書式設定→(オプションタブ)→「棒の間隔」を「0」にすればよい.) |
||||||||||||||