|
次の式(1)のような代数不等式も,「チェビシェフの(和の)不等式」と呼ばれるが,このページで扱うチェビシェフの不等式は,確率・統計に関するもので,互いに全く別の物です.
a<b, x<y ⇒ (a+b)(x+y)≦2(ax+by)・・・(1)
【チェビシェフの不等式】
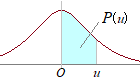
平均値m,標準偏差σの確率分布について,変数Xの値が|X−m|≦kを満たす確率をP(|X−m|≦k)で表すと
※kは,σよりも大きい定数(整数に限定されない)
|X−m|>kを満たす確率をP(|X−m|>k)で表すと あるいは,変数Xの値が|X−m|≦kσを満たす確率をP(|X−m|≦kσ)で表すと
※kは,1よりも大きい定数(整数に限定されない)
|X−m|>kσを満たす確率をP(|X−m|>kσ)で表すと |
 (解説)
(解説)起こり得るすべての場合の確率が1だから,「平均値mまでの距離がk以下」の確率が(1)式になることと,残りの「平均値mまでの距離がkよりも大きい」確率が(2)式になることとは,どちらか一方を示せば他方も成り立つ. また,「平均値mまでの距離がk以下」とするよりも「平均値mまでの距離が標準偏差σのk倍以下」という形で目盛りを考える方法もある.そこで(1)(2)でk=k’σを代入すると(1’)(2’)になり,これらを示してもよい. 以下では,(2’)を証明する. |
 (証明)
(証明)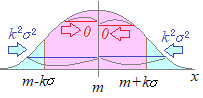 (証明)
(証明)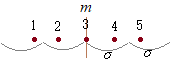

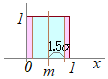
 (ⅱ) 直接計算する場合
(ⅱ) 直接計算する場合 (解説)
(解説)