■確率変数の変換

【以下の内容の要約】
　　確率変数の１次式で表わされる変数の期待値，分散，標準偏差は，元の確率変数の期待値，分散，標準偏差で表わすことができる．さらに，計算が簡単になるような変換で期待値，分散，標準偏差を求めてから，元の変数に戻すこともできる．
○　X, Y が確率変数，a，b が定数のとき
E(aX + b) = aE(X) + b　･･･(1)
V(aX + b) = a2 V(X)　･･･(2)　　（※ b は無関係)
σ(aX + b) = |a|σ(X)　･･･(3)　　（※ b は無関係)
E(aX + bY) = aE(X) + bE(Y)　･･･(4)
○　X, Y が独立な確率変数，a，b が定数のとき
E(XY) = E(X)E(Y)　･･･(5)
V(aX + bY) = a2V(X) + b2V(Y)　･･･(6)
.
【 解説 】　
(1)←
X x1 x2 … xn 1
aX+b ax1 + b ax2 + b … axn + b 1
P p1 p2 … pn 1

x1p1 + x2p2 + … + xnpn = E(X)，　p1 + p2 + … + pn = 1　のとき
E(aX + b)
= ( ax1 + b )p1 + ( ax2 + b )p2 + … + ( axn + b )pn
= ax1p1 + bp1 + ax2p2 + bp2 + … + axnpn + bpn
= a(x1p1 + x2p2 + … + xnpn) + b( p1 + p2 + … + pn )
= aE(X) + b

(2)←
{ ( x1 - E(X))2 + ( x2 - E(X))2 + … +( xn - E(X))2 } = V(X) のとき
V(aX + b) = { ( ax1 + b - aE(X) - b)2 + ( ax2 + b - aE(X) - b)2 + … + ( axn + b - aE(X) - b)2
= { a2( x1 - E(X))2 + a2( x2 - E(X))2 + … + a2( xn - E(X))2
=a2 V(X)

(3)←
σ(X) = 　のとき
σ(aX + b) = = = |a|σ(X)
(4)(5)(6)略

【 簡単な例 】
【例1】　２つの変数の組合わせごとに確率を考える（同時確率分布，結合確率分布）よりも，変数ごとに分けて考える方が簡単になる．

　2個のさいころを同時に投げたとき出る目の和の期待値，分散を求めたいとき

計算1のように直接求めれば，

のような複雑な計算になるが，

計算２から

を組み合わせると

のように，より簡単な計算で求まる．		 計算１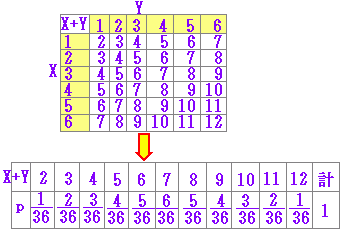





計算２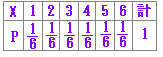
【例２】　仮平均を使った簡単な整数計算に直せる．

右のような度数分布表から期待値，分散を求めたいとき，
計算１は定義に従って計算する方法
計算２ は
　　(分散)=(X2の平均)-(Xの平均)2　で計算する方法
計算３ は
　仮平均 x0 = 155，階級幅 c = 10 として変数変換を行う方法
（手計算としては計算３ が最も楽）

■計算３の根拠■
Y　= aX + b で変数変換したとき
E(Y) = aE(X) + b　･･･(1)
V(Y) = a2 V(X)　･･･(2)
で期待値，標準偏差が求められる．

右の計算３において，仮平均 155，階級幅 10 とおくと
　X　= 10 u + 155 (u = 0，±1，±2，･･･)
となるから，簡単な整数 u で期待値，分散を求めておくと
(1)により E(X) = 10E(u) + 155
(2)により V(X) = 102 V(u)
となって，元の変数 X の期待値，分散が求まる．

■計算３の実際■
○　どの階級値を仮平均に選んでもよいが，計算を楽にするためには
ア)　「度数の大きな階級の階級値を仮平均とする」→「計算上0を掛けるので有利」，
イ)　「真ん中あたりの階級の階級値を仮平均とする」→±1，±2，･･･などの数字が小さくなるので計算が楽
のいずれかを考える．

○　u の値は，仮平均の階級を0として整数値を順に書き込むだけ
(※　平均は，仮平均から少しはずれるのは普通)

○　u の期待値，分散の計算も
(分散)=(X2の平均)-(Xの平均)2　で計算するのが楽		 計算1
階級 階級値(x) 度数(f) xf (X-m)2f
130-140 135.0 3 405 1250.5
140-150 145.0 5 725 542.5
150-160 155.0 7 1085 1.2
160-170 165.0 6 990 551.0
170-180 175.0 3 525 1150.5
計 　 24 3730 3495.8
E(X)=3730÷24=155.4
V(X)=3495.8÷24=145.7
計算２
階級 階級値(x) 度数(f) xf x2f
130-140 135.0 3 405 54675
140-150 145.0 5 725 105125
150-160 155.0 7 1085 168175
160-170 165.0 6 990 163350
170-180 175.0 3 525 91875
計 　 24 3730 583200
E(X)=3730÷24=155.4
V(X)=E(X2)-E(X)2=583200÷24 - 155.42 = 145.7
計算３
階級 階級値(x) 度数(f) u uf u2f
130-140 135.0 3 -2 -6 12
140-150 145.0 5 -1 -5 5
150-160 155.0 7 0 0 0
160-170 165.0 6 1 6 6
170-180 175.0 3 2 6 12
計 　 24 　 1 35
E(u) = 1÷24=0.042
V(u) = E(u2)-E(u)2 = 35÷24 - 0.0422 = 1.457
E(X) = 155.0 + 10×0.042=155.4
V(X) = 102×1.457=145.7
■簡単な穴埋め問題■
(1)
　確率変数 X の期待値が50で，分散が100のとき，
Y　= 2X + 10 を満たす確率変数 Y の期待値と分散を求めよ．
　期待値 ，分散

(2)
　１個のさいころを投げたとき出る目の期待値は 3.50 で，分散は 2.92 である．これを用いて，３個のさいころを同時に投げたとき，出る目の和の期待値と分散を小数第２位を四捨五入して小数第１位まで求めよ．
　期待値 ，分散

　この結果を，１個のさいころの出た目の3倍の値の期待値，分散と比較すると
　　期待値　：　[ 等しい | 等しくない ]
　　分散　　：　[ 等しい | 等しくない ]

(3)
　アンケート調査の結果を集計するときに，
Ａ)　非常によい：5，よい：4，普通：3，悪い:2，非常に悪い：1と数値化する場合
Ｂ)　非常によい：2，よい：1，普通：0，悪い：-1，非常に悪い：-2と数値化する場合
の２つを比較すると，期待値，標準偏差は同じになるか．

　　期待値　：　[ 等しい | 等しくない ]
　　標準偏差　　：　[ 等しい | 等しくない ]

また，次のＣ)とＡ)を比較すると，期待値，標準偏差は同じになるか．
Ｃ)　非常によい：50，よい：40，普通：30，悪い：20，非常に悪い：10と数値化する場合

　　期待値　：　[ 等しい | 等しくない ]
　　標準偏差　　：　[ 等しい | 等しくない ]
(4)
　次の表は，度数分布表から仮平均を用いて期待値と分散を求めるものである．空欄を埋めよ．
階級 階級値(X) 度数( f ) u uf u2f
40-50 45.0 5 -2 -10 20
50-60 55.0 10 -1 -10 10
60-70 65.0 14 0 0 0
70-80 75.0 9 1 9 9
80-90 85.0 2 2 4 8
計 　 40 　 -7 47
※小数第2位まで求めよ．
E(u) =
V(u) =
E(X) =
V(X) =

確率統計のメニューに戻る 高校数学のメニューに戻る