現在地と前後の項目

確率変数と確率分布(1)/確率変数，確率分布(2)/期待値/分散，標準偏差/期待値，分散，標準偏差/代表値（平均値，中央値，最頻値）/度数分布表→平均値,分散,標準偏差/度数分布表をExcelで/度数分布表，相対度数分布表/分割表(クロス集計表)，散布図の作成/散布図とクロス集計/確率変数の変換(1)/確率変数の変換(2)/同時確率分布，周辺分布/資料の散布度/共分散,相関係数/チェビシェフの不等式/ベクトルの内積と相関係数/二項分布/連続型確率分布/正規分布(1)/正規分布(2)/二項分布の正規近似/母平均,母比率の推定/同［練習問題］/母平均，母比率の検定(大標本)/母集団，標本/総和記号Σ(シグマ)に慣れよう(1)/総和記号Σ(シグマ)に慣れよう(2)/センター試験.確率分布 統計(2013年～)/

■　Σ記号に慣れよう(Σ記号の値をExcelで求めるには)

■解説

(1)　10Σk = 1Σik を数値で求めるには：


　右図のようにセルA1に1，A2に2，･･･，A10に10を書き込んでおき(*1)，セルA11に関数
=SUM(A1:A10)
を書き込む(*2)．セルA11の値が答．
（初歩的な参考）
(*1)　セルA1～A10に，1～10を書き込むには
  • A1に１を書き込む
  • A1～A10をドラッグにより反転表示にする
  • メニューから「編集」→「フィル」→「連続データの作成」→「範囲：列，種類：加算，増分値：1　ＯＫ」
(*2)　セルA11に =SUM(A1:A10) を書き込むには，次のうちいずれか１つのの操作を行えばよい（１つだけ）
  1. セルA11をポイントし，ショートカットアイコンのΣをクリックする．（この問題のように連続データに続くセルでΣをクリックすると，自動的に隣接する数値データの範囲全体を加えることが多いが，求めるものと異なるときは，引き続いてドラッグし直すとよい．）
  2. メニューから「挿入」→「関数」→「数学／三角でSUM」→「数値1のところでをクリックし，A1～A10までをドラッグ（数値2の欄は空白のままにする）」
  3. セルA11に半角英数字で直接 =SUM(A1:A10) と書き込む（A1とA10の間にはセミコロン(;)でなく，コロン(:)を書き込む）
.
(2)　10Σk = 1Σik2 を数値で求めるには：
  • 右図のようにセルA1に1，A2に2，･･･，A10に10を書き込んでおき(上の例(1))，
  • 次に，セルB1に =A1^2 （^2は2乗を表わす）と書き込む
  • セルB1をポイントし，右下でマウスの形が＋になったら，B10までドラッグする（または，B1をコピーし，B2からB10までに貼り付ける=数式の貼り付けにより各々のセルの左のセルの値の２乗が得られる）．
  • セルA11に関数
    =SUM(B1:B10)
    を書き込む．セルB11の値が答．
(3)　右のようにA1～A5に数値 x1～x5 が書き込まれていて，これらの平均値を m とするとき，

.5Σk = 1Σi(xk−m)2

を求めるには：
  • まず平均値 m をセルA6に書き込む：
    • セルA6に=AVERAGE(A1:A5) と書き込む．
    • または，メニューから「挿入」→「関数」→「統計」→「AGERAGE」→「数値1のところでをクリックし，A1～A5までをドラッグ（数値2の欄は空白のままにする）」
  • 次に，セルB1に
    =(A1-$A$6)^2
    と書き込む．（$A$6とするところが重要．今の場合A$6でもよいが，とにかく式のコピー&貼り付けをするときに，平均値のセルA6が動かないことが重要）
  • セルB1をポイントし，右下でマウスの形が＋になったら，B5までドラッグする（または，B1をコピーし，B2からB5までに貼り付ける）．
  • セルB6に関数
    =SUM(B1:B5)
    を書き込む．セルB6の値が答．

■問題１　上の解説を参考にして，Excelを用いて次の値を求めなさい．

(1)

. 10Σk = 1Σi(2k+1) =



(2)

. 10Σk = 1Σi(2k−1)2 =


(3)
　右図のようにA1～D1に数値 x1～x4 が書き込まれていて，A2～D2に数値 y1～y4 が書き込まれているとき，


.4Σk = 1Σi(xk−yk )2

の値を求めなさい．（右図の値で計算しなさい）

.



解説 統計でよく使われる量とExcelでの計算
統計で使われる量 Excelでの計算
○　平均値
　n個の変数 x1，x2，x3，･･･，xn の平均値 mは，


.m = .1nn{x1+x2+x3+･･･++xn}
で定義される．
　Σ記号を用いれば，
.m = .1nnnΣk = 1Σixk
と書ける．		 　次のように，変数x1，x2，x3，･･･，x5 の値がセルA1～A5に入力されているとき，

.
これら5つの変数の平均値は，=AVERAGE(A1:A5) で求められる．
（　=SUM(A1:A5)/COUNT(A1:A5) に等しい　）
○　変動（偏差平方和）

　n個の変数 x1，x2，x3，･･･，xn の平均値を mとするとき，変動（偏差平方和） S は

.S=(x1−m)2+(x2−m)2+(x3−m)2+･･･+(xn−m)2

で定義される．
　Σ記号を用いれば，

. S=nΣk = 1Σi(xk−m)2
と書ける．		 　次のように，変数x1，x2，x3，･･･，x5 の値がセルA1～A5に入力されているとき，

.
これら5つの変数の変動は，
(1) A6 に平均値を求める：=AVERAGE(A1:A5)
(2) B1に=(A1-$A$6)^2と書き込むみ，B5までコピー貼り付け
(3) B6に=SUM(B1:B5) ･･･これが変動
○　分散
　分散はデータのばらつき具合を表わす量で，n個の変数 x1，x2，x3，･･･，xn の分散は，平均値を mとするとき


.V = .1nn{(x1−m)2+(x2−m)2+(x3−m)2+･･･+(xn−m)2}

で定義される．
　これはΣ記号を用いて，

.V = .1nnnΣk = 1Σi(xk−m)2
と書ける．

※　上に述べた変動（偏差平方和） S との関係は


. S=nV , V=.Snn
 　次のように，変数x1，x2，x3，･･･，x5 の値がセルA1～A5に入力されているとき，

.
これら5つの変数の分散は，=VARP(A1:A5) で求めることができる．
　Excelのメニューから関数を選択するときは，メニュー→「挿入」→「関数」→「統計」→VARP
※　Excel関数として，よく似たものが他にもあるので注意
※　分散は，1つの関数で直接求められるようになっている．
※　これを用いれば，上に述べた変動（偏差平方和）は，
=VARP(範囲)*個数で求められる．
○　不偏分散
　分散と同様にデータのばらつきを表わす量であるが，n個の変数 x1，x2，x3，･･･，xn が母集団から取られた標本であるとき，母集団の分散の推定値を不偏分散という．
　不偏分散は，


..1n-1nnn{(x1−m)2+(x2−m)2+(x3−m)2+･･･+(xn−m)2}

で定義される．
　これはΣ記号を用いて，

..1n-1nnnnΣk = 1Σi(xk−m)2
と書ける．
※　不偏分散の方が単純に求めた分散よりも少し大きい．
※　（不偏分散）×(n -1)=変動=(分散)×(n) が成り立つ．		 　次のように，変数x1，x2，x3，･･･，x5 の値がセルA1～A5に入力されているとき，

.
これら5つの変数の不偏分散は，=VAR(A1:A5) で求められる．
　Excelのメニューから関数を選択するときは，メニュー→「挿入」→「関数」→「統計」→VAR
※　Excel関数として，よく似たものが他にもあるので注意
○　（単純）標準偏差
　n個の変数 x1，x2，x3，･･･，xn の標準偏差 s は，平均値を mとするとき，
s=.√.1nn{(x1−m)2+(x2−m)2+(x3−m)2+･･･+(xn−m)2}√nnnnnnnnnnnnnnnnnnni

　これは，Σ記号を用いて，

. s=.√.1nnnΣk_=_1Σi(xk−m)2√nnnnnni

と書ける．
※　上に述べた分散 V との関係は，

. s2=V
　次のように，変数x1，x2，x3，･･･，x5 の値がセルA1～A5に入力されているとき，

.
これら5つの変数の標準偏差は，=STDEVP(A1:A5) で求められる．
　Excelのメニューから関数を選択するときは，メニュー→「挿入」→「関数」→「統計」→STDEVP
※　Excel関数として，よく似たものが他にもあるので注意
○　（標本からの推定した母集団の）標準偏差
　n個の標本 x1，x2，x3，･･･，xn から推定される母集団の標準偏差 σ は，平均値を mとするとき，
σ=.√_.1n-1nn{(x1−m)2+(x2−m)2+(x3−m)2+･･･+(xn−m)2}√nnnnnnnnnnnnnnnnnnnni

　これは，Σ記号を用いて，

.σ=.√_.1n-1nnnΣk_=_1Σi(xk−m)2√nnnnnnni

と書ける．
※　上に述べた不偏分散の正の平方根となっている．
 　次のように，変数x1，x2，x3，･･･，x5 の値がセルA1～A5に入力されているとき，
これら5つの標本から推定される母集団の標準偏差は，=STDEV(A1:A5) で求められる．
　Excelのメニューから関数を選択するときは，メニュー→「挿入」→「関数」→「統計」→STDEV
※　Excel関数として，よく似たものが他にもあるので注意
○　ベクトルの内積（Excelの用語では配列の積）
　２つのベクトル
−−>uw=(x1 , x2 , x3 , ... , xn)
−−>vw=(y1 , y2 , y3 , ... , yn)
の内積は，

.−−>uw·−−>vw=x1y1+x2y2+x3y3 ... + xnyn

で定義される．
　これは，Σ記号を用いて，

.−−>uw·−−>vw=nΣk = 1Σixkyk
と書ける．

　ベクトル −−>uw=(x1 , x2 , x3 , ... , xn) の大きさ |−−>uw| は，

.|−−>uw|=.√x12+x22+x32_..._+_xn2√nnnnnnnnni

で定義される．
　これはΣ記号を用いれば，

.|−−>uw|=.√nΣk_=_1Σixk2√nnni
と書かれる．
.

　次のように，ベクトル −−>uw　の成分 x1，x2，x3，･･･，x5 がセルA1～A5に入力されており，
　ベクトル −−>vw　の成分 y1，y2，y3，･･･，y5 がセルB1～B5に入力されているとき，
これら２つのベクトルの内積 −−>uw·−−>vw は，
=SUMPRODUCT(A1:A5,B1:B5) で求めることができる．
　　［　積（PRODUCT）の和（SUM）の意味　］
　Excelのメニューから関数を選択するときは，メニュー→「挿入」→「関数」→「数学／三角」→SUMPRODUCT
（配列１にA1:A5，配列2にB1:B5を指定する．配列3は空白）

※　SUMPRODUCTは要素数が等しい列と列，行と行に使える．
※　C1に=A1*B1とし，この式をC2からC5にコピー貼り付けの後，C6に=SUM(C1:C5) としても同じ結果が得られる．

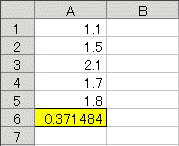
■問題2　上の解説を参考にして，Excelを用いて次の値を求めなさい．

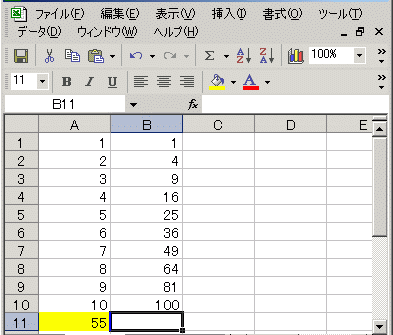
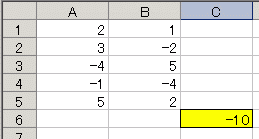
　右の表において，セルA1～A10に入力されている値を，各々x1 , x2 , x3 , ... , x10 とし，セルB1～B10に入力されている値を各々y1 , y2 , y3 , ... , y10 とするとき，次の値を求めなさい．
　なお，これらの値を転記するには，画面上でドラッグ・コピーし，Excel上に貼り付けるとよい．
　
(1)　.110nn10Σk = 1Σixk=


(2)　x1 , x2 , x3 , ... , x10 の平均値を m とするとき，

　　　10Σk = 1Σi(xk−m)2=


(3)　　x1 , x2 , x3 , ... , x10 の平均値を m とするとき，

　　　.110nn10Σk = 1Σi(xk−m)2=


(4)　　　x1 , x2 , x3 , ... , x10 の平均値を m とするとき，

　　　.19n10Σk = 1Σi(xk−m)2=

(小数第2位まで求めなさい．)

(5)　　10Σk = 1Σixkyk=


(6)　　x1 , x2 , x3 , ... , x10 の平均値を m ，y1 , y2 , y3 , ... , y10 の平均値を n とするとき，

　　　10Σk = 1Σi(xk−m)(yk−n)=


(7)　　x1 , x2 , x3 , ... , x10 の平均値を mとするとき，

　　　.√_.19n10Σk_=_1Σi(xk−m)2√nnnnnnni=


(小数第2位まで求めなさい．)
　 A B
1 3 1
2 4 -2
3 4 3
4 5 2
5 5 -2
6 5 4
7 6 -1
8 6 -3
9 7 2
10 8 3
























...メニューに戻る
■このサイト内のGoogle検索■

△このページの先頭に戻る△
【 アンケート送信 】
… このアンケートは教材改善の参考にさせていただきます

■この頁について，良い所，悪い所，間違いの指摘，その他の感想があれば送信してください．
○文章の形をしている感想は全部読ませてもらっています．
○感想の内で，どの問題がどうであったかを正確な文章で伝えていただいた改善要望に対しては，可能な限り対応するようにしています．（※なお，攻撃的な文章になっている場合は，それを公開すると筆者だけでなく読者も読むことになりますので，採用しません．）


質問に対する回答の中学版はこの頁，高校版はこの頁にあります