|
現在地と前後の項目 確率変数と確率分布(1)/確率変数，確率分布(2)/期待値/分散，標準偏差/期待値，分散，標準偏差/代表値（平均値，中央値，最頻値）/度数分布表→平均値,分散,標準偏差/度数分布表をExcelで/度数分布表，相対度数分布表/分割表(クロス集計表)，散布図の作成/散布図とクロス集計/確率変数の変換(1)/確率変数の変換(2)/同時確率分布，周辺分布/資料の散布度/共分散,相関係数/チェビシェフの不等式/ベクトルの内積と相関係数/二項分布/連続型確率分布/正規分布(1)/正規分布(2)/二項分布の正規近似/母平均,母比率の推定/同［練習問題］/母平均，母比率の検定(大標本)/母集団，標本/総和記号Σ(シグマ)に慣れよう(1)/総和記号Σ(シグマ)に慣れよう(2)/センター試験.確率分布 統計(2013年～)/ 試行の結果によって，その値をとる確率が定まる変数を確率変数という．確率変数とその値をとる確率との対応を示したものを確率分布という．確率変数が整数値などの離散的な値（とびとびの値）になるときは，確率分布は，次のような一覧表で示されることがある．
|
|||||||||||||||||||||
| ※ 試行の結果として起こる事象に整数や実数の数値が結びつけられているときに，その数値を確率変数という．この場合において，事象を決めれば，数値も確率も決まることが重要． ○例１ 100本のくじで，１等10000円が2本，2等1000円が8本，3等100円が10本，残りがはずれとなっている場合に，このくじをよくまぜてから１本引いて起こる事象，賞金，確率は，次の表のようになる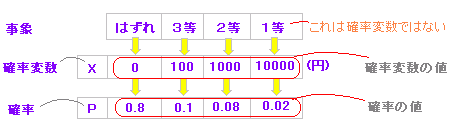．  ×例２ 100人の生徒の血液型が，Ａ型40人，Ｂ型20人，ＡＢ型10人，Ｏ型30人であったとき，これらの血液型について，度数分布表，相対度数分布表を作ることはでき，１人抽出したときの各血液型の生徒が選ばれる確率は定まるが，Ａ型，Ｂ型，ＡＢ型，Ｏ型などは確率変数ではない．  (グラフ中の赤線で示した値は，単に度数の平均を表わしており，確率変数の平均として想定されるものがあるとすれば，グラフ中の青線のようなものとなる．血液型の平均値はない．） この例のように，定性的な性質で分類したデータ（カテゴリーデータ）の分類名（カテゴリー）は，そのままでは確率変数には使えない． ×例３ ある授業のわかりやすさについて100人の生徒にアンケート調査をしたところ，次のような結果が得られたとする．
|
|||||||||||||||||||||
| ○ 記号 確率変数 X が x k という値をとる確率を P(X = x k) で表わす． 確率変数 X が a ≦ X ≦ b の範囲の値をとる確率を P(a ≦ X ≦ b) で表わす． （a ＜ X ＜ b の範囲には P(a ＜ X ＜ b)， X ＞ a の範囲には P（X ＞ a) が対応する．） |
|||||||||||||||||||||
| 例４ 上の例１で，賞金10000円がもらえる確率は， P(X = 10000) = 0.02 となる． 例５ さいころを１回投げて，出た目の数の100倍の金額（円）がもらえる場合，確率分布は次の表のようになる．
この場合，さいころを１回投げて，２００円もらえる確率は P(X = 200) =  16同様にして，１００円以上３００円以下となる確率は P(100 ≦ X ≦ 300) = 12同様にして，500以上となる確率は P( 500 ≦ X ) = 13 |
確率統計のメニューに戻る