|
■ ベクトルの内積 (高卒文系向き:Excelで求める方法) (高校の数学ではベクトルは3次元までを扱うが,以下の記述はその制限にとらわれず文系で高卒程度の学生を念頭に置いてn次元ベクトルについて述べる.) 高校の数学では,ベクトルの内積は2つのベクトルのなす角 θ を用いて定義され,ベクトルの成分を用いた表現はその結果として証明されるのが普通である.  文系の生徒から見れば,右図のような矢印ベクトルを用いる場面は多くなく,この説明方法では分かりにくいことがある.そこで,ベクトルの成分表示を中心にして,成分からベクトル内積を説明してみる.(このときの角度 θ の意味は後で述べる.) |
(高校数学Bにおけるベクトル内積の定義) · =|| ||cosθ 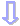 (θ は,ベクトル , のなす角 0°≦θ°≦180° ) (ベクトル内積の性質) =(x1 , y1 ) , =(x2 , y2 ) のとき, · =x1x2+y1y2 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ■成分を用いたベクトル内積の定義 ○ 右の表1において,単価を順に並べたものをベクトル で表わすことにすると,=(130, 150, 80, 150) になる. また,購入個数を順に並べたものをベクトル で表わすことにすると,=(2, 3, 0, 4) になる.(みかんは購入していない.) このとき代金は 130·2+150·3+80·0+150·1=1190(円)となるが,これをベクトル , の内積であらわすことにする. すなわち,· =130·2+150·3+80·0+150·1=1190 ○ 右の表2は,職種によって時間給が異なるA,B,C,D,Eの5人のパートタイマーの時間給と勤務した時間の一覧表とする.このとき,時間給ベクトルを で表わすことにすると,=(780, 800, 850, 850, 910) になる. また,勤務時間のベクトルを で表わすことにすると,=(8, 7.5, 5, 3, 3) になる. このときこの日の給料合計は 780·8+800·7.5+850·5+850·3+910·3=21780(円)となるが,これをベクトル , の内積であらわすことにする. すなわち,· =780·8+800·7.5+850·5+850·3+910·3=21780
○ ベクトルの定義
何番目の成分が何を表わすかを決めておいて,数字を並べたものをベクトルといい,単なる1つの数と区別するために上に矢印を付けた記号で表わす. =(x1 , y1 , z1 , … ) , =(x2 , y2 , z2 , … ) など 例 =(130, 150, 80, 150) ○ ベクトルの内積の定義 2つのベクトルの成分の個数が等しいとき,「成分の積の和」をベクトルの内積という. =(x1 , y1 , z1 , … ) , =(x2 , y2 , z2 , … ) のとき, · =x1 x2+y1 y2+z1 z2+… 例 =(1, 2, 3) , =(4, 5, 6) のとき, · =1·4+2·5+3·6=4+10+18=32 ※注意 ベクトル とベクトル との内積を表わすには, 2 と書かずに,· と書く. ベクトルの積には,内積 · の他に外積 × もあり,2 のような記号を使うと,どちらなのか区別できなくなるので,使わないと考えるとよい. |
表1
=(2, 3, 0, 4) ※ ベクトルの何番目の成分がどの果物に対応するか決められているので,=(130, 150, 80, 150) とすることと,=(150, 130, 80, 150) とすることでは,別の内容になることに注意.このことは, についても同様で,成分を入れ替えると各々の果物の個数が変る点に注意. 表2
=(8, 7.5, 5, 3, 3) ※ ベクトルを図形的に矢印で定義すると4次元(成分の個数が4個)以上のベクトルをイメージしにくいが,左のようにベクトルを定義すると何次元になっても平気である. 表3
=(40, 50, 60) 人数(統計では度数ということが多い)ベクトルを =(10, 25, 5) とおくと,合計得点は · =40·10+50·25+60·5=1950 になる. 表4 各得点の人数を合計人数で割ると,一人選んだときにその得点である確率を表わす.
=(40, 50, 60) 確率ベクトルを =(, , ) とおくと,平均得点は · =40·+50·+60·= になる. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ■Excelを用いた内積の計算 右の表5のように,A1〜E1にベクトル の成分 (1, 3, 5, 2, 4) が入力してあり,A2〜E2にベクトル の成分 (2, 1, 3, 0, 2) が入力してあるとき,これらのベクトルの内積 · をF3に書き込むには,次の(ア)の方法で素朴に行えるが,内積の計算がしばしば登場するときにはこれでは不便なので,(イ)のようにExcelの組み込み関数 SUMPRODUCTを使うと楽に求められる.(積:PRODUCTの和:SUMで積の和,すなわち内積になる) (ア) 単純に「積の和」を組み立てていく方法 A3に =A1*A2と書き込み,これをコピーしB3〜E3に貼り付け.次にF3にそれらの和を求める計算式 =SUM(A3:E3)を書き込む. (イ) 内積を求める関数SUMPRODUCTを使う方法 F3に=SUMPRODUCT(A1:E1,A2:E2)と書き込む. ( 直接書き込んでもよいし,fx を押してから,対話型メニューに従って順次範囲を入力していってもよい) ※ ベクトルの成分が表6のように2つとも縦型に書かれているときは,内積を書き込みたいセルに =SUMPRODUCT(A1:A5,B1:B5) とすればよい. ※ 上の例のように,関数SUMPRODUCT は行ベクトル(行で表わしたベクトル)と行ベクトルの内積,または,列ベクトル(列で表わしたベクトル)と列ベクトルの内積を求めるのに使う.行ベクトルと列ベクトルの内積は =SUMPRODUCTでは計算できない. 行ベクトルと列ベクトルの内積は,1×n行列とn×1行列の積と考えて,=MMULT とすればよい.右の表7において,行ベクトルA3:E3と列ベクトルF1:F5の内積は =MMULT(A3:E3,F1:F5) で求められる. |
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
■ベクトルの大きさと向き ○ ベクトル =(x , y , z , … ) の大きさを || で表わし, ||== で定義する. ○ 2つのベクトル =(x1 , y1 , z1 , … ) , =(x2 , y2 , z2 , … ) について, cosθ== (0°≦θ≦180°)となる角度θ を2つのベクトルのなす角と定義する. ·= ※ この角度θ は,4次元以上のベクトルについては視覚的に想像することはむずかしい.実際には,cosθ の値 だけでよい.
θ が0°〜180°まで変化するとき,cosθ の値は1〜-1まで変化する.
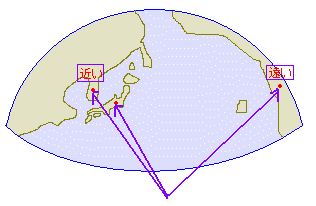
特に,cos0°=1, cos90°=0,cos180°=-1が重要な値で, 0°に近いほどcosθ の値は1に近く,180°に近いほどcosθ の値は−1に近い.90°(直角)のときcosθ の値は0になる.  この値は後に述べるように相関係数を表わし,1に近いとき2つのベクトルは似ている(正の相関),-1に近いとき逆向き(負の相関),0に近いとき無関係と考える. 例 地球の中心を原点とするxyz座標で見れば,東京とソウルは近く,東京とロサンゼルスは遠い.この根拠は,この数字(cosθ )が1に近いかどうか(各々0.98 , 0.17 )で示せる.
|
次のような試験結果から,国語,数学,英語の相関,生徒ごとの得点の類似度を考えることができる.(架空データ) 表8
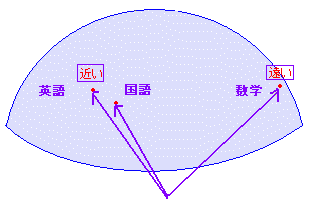 個人ごとの得点状況の類似性を考えるには,上記の表で行方向にとったベクトルの相関(すなわちcosθ の値)を見ればよく,次のような表からNo.1の生徒はNo.2 , No.5 , No.9の生徒とよく似た得点状況であるが,No.3 , No.4 , No.8の生徒とは異質であると判断できる.(No.2以下についても同様に見ることができる.ただし,自分自身との相関係数は常に1となる.) 表9
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ■Excelを用いた角度の計算(角度θ まで求める必要はない・・・cosθ,もしくは相関係数を求める) ○ 右の表10において,東京のxyzベクトル =(-3936 , 3374 , 3684 ) とソウルのxyzベクトル =(-3030 , 4035 , 3872 ) との内積 · を求めるには,上述のように =SUMPRODUCT(B2:D2,B3:D3) が使える. ○ 東京のxyzベクトルの大きさの2乗(自分自身との内積)は,=SUMSQ(B2:D2) で求められるので,ベクトルの大きさはその正の平方根として =SQRT() で求められる.したがって, ||=SQRT(SUMSQ(B2:D2)) ||=SQRT(SUMSQ(B3:D3)) ○ 以上から, cosθ =SUMPRODUCT(B2:D2,B3:D3)/(SQRT(SUMSQ(B2:D2)) *SQRT(SUMSQ(B3:D3)) =0.984 となる. |
表10
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| ■相関係数とcosθ の関係 相関係数は,各成分を平均値からの増減で表わしたときのcosθと一致する.
□ 相関係数を求めるには ○ 表11のB1:D10から,各教科の相関係数を求めるには, Excel2002では,ツール→分析ツール(Excel2007では,データ→データ分析) →相関→OK →入力範囲: A2:D10 →データ方向:(このデータで教科相互の相関を見るには)列方向 →先頭行をラベルとして使用 →OK これにより,次の表12のような相関係数が得られる.
○ 個別に国語と数学の得点の相関係数を求めるには,=CORREL(B2:B10,C2:C10) でよいが,系列が多数あるときは,組合せが多くなるので上記のように分析ツール(またはデータ分析)を用いるとよい. □ ここで求めた相関係数は,実は国語の得点の列ベクトル(B2,B3,...,B10)と数学の得点の列ベクトル(C2,C3,..,C10)から求めたcosθとは,そのままでは一致しない. 右図のように原点(0点)を基準としてみると全員上の方に見えて,「どの生徒もよくできる生徒ばかりで・・・」と,生徒間の差異が分からない.そこで,相関係数を求めるときは,表11のF2〜H10のように各々の平均点を引いた値を用いて計算する. ○ 国語' のベクトル(F2,F3,...,F10)と数学' のベクトル(G2,G3,...,G10)について = を求めると,これが上で求めた相関係数と一致する.(分析ツールまたはデータ分析では,これらの操作は自動で行われるので,元のデータを直接代入するだけで結果が得られる.) |
表11
図 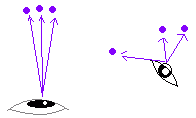 ※ 表11から生徒間で得点状況の類似性を調査するには,行ベクトル(B2〜D2など)の相関(cosθの値)を調べることになるので, Excel2002では,ツール→分析ツール(Excel2007では,データ→データ分析) →相関→OK →入力範囲: A2:D10 →データ方向:(このデータで生徒間の得点の類似性を見るには)行方向 →先頭行をラベルとして使用 →OK これにより,上の表9のような相関係数が得られる. |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||