�x�N�g���̓���
�m����n���@�x�N�g���̂Ȃ��p
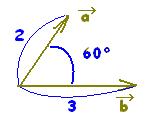
�Q�̃x�N�g�� �̎n�_�����_O�ɏd�˂āC
�̎n�_�����_O�ɏd�˂āC �Ƃ���Ƃ��C��AOB=�����x�N�g����
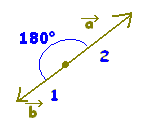
�Ƃ���Ƃ��C��AOB=�����x�N�g���� �̂Ȃ��p�Ƃ����B�������C0�����Ɓ�180���Ƃ���B
�̂Ȃ��p�Ƃ����B�������C0�����Ɓ�180���Ƃ���B


�Q�̃x�N�g��,\hspace{5}\vec{b}=(b_1,b_2)) �̂Ȃ��p�����Ƃ���Ƃ��C�x�N�g��
�̂Ȃ��p�����Ƃ���Ƃ��C�x�N�g�� �̓���
�̓��� �����̎��Œ�`����B
�����̎��Œ�`����B
 �E�E�E(1)
�E�E�E(1)
 �E�E�E(2)
�E�E�E(2)
��̒�`�ɂ����āC(1)�͖��ŕ\�����}�`�x�N�g���ɑΉ����C(2)�͐����\���ɑΉ����܂��D
���Z�̋��ȏ��ł́C���߂ɖ����g���ăx�N�g����}�`�I�ɓ������܂��̂ŁC(1)���`�Ƃ���(2)�����ʂƂ��܂��D
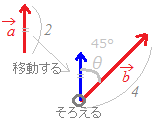
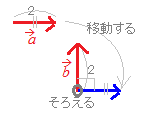
�������C���̃y�[�W�̏�����̕��i���j�ɏ����Ă��܂��悤�ɁC�����ŕ\�����x�N�g�����ɏK�����ꍇ�C(2)���`�Ƃ���(1)�����̐����Ƃ��邱�Ƃ��ł��܂��D
�������C���̃y�[�W�̏�����̕��i���j�ɏ����Ă��܂��悤�ɁC�����ŕ\�����x�N�g�����ɏK�����ꍇ�C(2)���`�Ƃ���(1)�����̐����Ƃ��邱�Ƃ��ł��܂��D




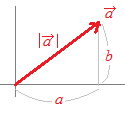 �@�܂��C
�@�܂��C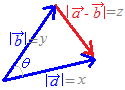 �@���ɁC�E�}�̂悤�ȎO�p�`�ɂ��ė]���藝���v���o����
�@���ɁC�E�}�̂悤�ȎO�p�`�ɂ��ė]���藝���v���o����