== 内積を用いたベクトル方程式 ==
※直線の方程式は,「方向ベクトル」で表す方法と,「法線ベクトル」で表す方法があります。この頁では「法線ベクトル」で表す方法を取り扱っています.
[要点]
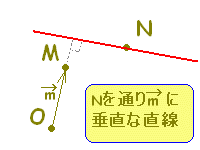
○平面上において点 Aを通り法線ベクトル  \( \vec{n} \) \( \vec{n} \)に垂直な直線の方程式は,
=0&chco=0000ff) \( \vec{n}\cdot (\vec{p}-\vec{a})=0 \) \( \vec{n}\cdot (\vec{p}-\vec{a})=0 \)…(1)
※ 「法」という言葉は,縦の関係に使われます。
「法面工事中」「法令」などの法は縦の関係です。

※ 数学では,接線と法線が分かればOKです。

|
[解説]
(1)←
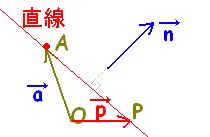
 \( \overrightarrow{\rm{AP}}\perp \vec{n} \) \( \overrightarrow{\rm{AP}}\perp \vec{n} \)ならば Pは Aを通り  \( \vec{n} \) \( \vec{n} \)に垂直な直線上にあります。
また, Aを通り  \( \vec{n} \) \( \vec{n} \)に垂直な直線上にあれば,
 \( \overrightarrow{\rm{AP}}\perp \vec{n} \) \( \overrightarrow{\rm{AP}}\perp \vec{n} \)が成り立ちます。
2つのベクトルが垂直(直角)となる条件は (内積)=0 の関係で表せるので,以上の関係は
 \( \vec{n}\cdot\overrightarrow{\rm{AP}}=0 \) \( \vec{n}\cdot\overrightarrow{\rm{AP}}=0 \)
すなわち
=0&chco=0000ff) \( \vec{n} \cdot (\vec{p}-\vec{a})=0 \) \( \vec{n} \cdot (\vec{p}-\vec{a})=0 \)…(1)
で表せます.
(ここで, は は です.直線の中に埋まっている です.直線の中に埋まっている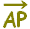 のことではないので注意しましょう。) のことではないので注意しましょう。)
|


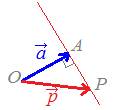
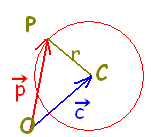 ○平面上において点
○平面上において点

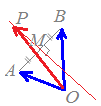
 ※この問題には,次のような別解があります.
※この問題には,次のような別解があります.