== 正規分布 ==
【標準正規分布】…平均0,標準偏差1の正規分布
統計において最も重要で,最もよく登場するのが正規分布(ガウス分布)です.特に,平均が0,標準偏差が1となる正規分布のことを標準正規分布といいます.
標準正規分布は
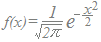 という指数関数で表されますが,統計の問題を扱うときに
という指数関数で表されますが,統計の問題を扱うときに
○ この関数形を覚える必要はありません.左右対称な帽子形(富士山形)だということが分かれば十分です.
○ この関数は筆算で積分することはできませんので,正規分布を利用するには,あらかじめコンピュータで数値積分として求められている数表(正規分布表)を使います.
○ 正規分布の問題は正規分布表を見ながら解くのが基本です.小数の足し算・引き算ができれば問題は解けます.重要なのは,「ノリとハサミ」の感覚です.
 ○ P(a<z<b)という記号によって, a<z<bとなる確率を表します.
正規分布では z=aと z=bの間にある確率が右図のような図形の面積で表されます.
すなわち, P(a<z<b)が右図の水色で示した図形の 面積になります.
次の点に注意してください.
 ○ 曲線の下にある図形の面積全部で確率 1を表しますが,グラフが左右対称になっているので,右半分,左半分の面積はそれぞれ 0.5になります.
○ z=aや z=bという縦線(直線)には幅がなくその面積は 0なので,
P(a<z<b)
というように不等号で表されている場合と
P(a≦z≦b)
というように等号付き不等号で表されている場合とは「どちらでも同じです」.
【問題1】
変数zが標準正規分布に従うとき,次の確率を求めてください.
(上で述べたように数学的にはP(a<z<b)とP(a≦z≦b)は同じになりますが,以下の問題では等号なしの形で出題します.)
|
 1【標準正規分布の累積関数】
0<u<3.10 1【標準正規分布の累積関数】
0<u<3.10の範囲内の小数 uを入力すれば,確率 P(0<z<u)を返します.
…右図の水色の面積
(uは小数第2位まで.求まる確率は小数第4位まで.)
求めるやり直す
 2【標準正規分布の累積関数の逆関数】
0<P<0.4990 2【標準正規分布の累積関数の逆関数】
0<P<0.4990の範囲内の小数 Pを入力すれば,確率 P(0<z<u)の値が Pとなる小数 uを返します.
…右図のuの値
(Pは小数第4位まで.uは小数第2位まで.)
求めるやり直す
3【正規分布表】
小数第1位までを左欄から小数第2位を上欄からそれぞれ読み取り,交わった欄の値を読み取ります.例えば,u=1.96のとき確率P(0<z<u)を求めるには,表の中で赤字で示した欄を読み取り,P(0<z<1.96)=0.4750とします.
| u |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
| 0.0 |
0.0000 |
0.0040 |
0.0080 |
0.0120 |
0.0160 |
0.0199 |
0.0239 |
0.0279 |
0.0319 |
0.0359 |
| 0.1 |
0.0398 |
0.0438 |
0.0478 |
0.0517 |
0.0557 |
0.0596 |
0.0636 |
0.0675 |
0.0714 |
0.0753 |
| 0.2 |
0.0793 |
0.0832 |
0.0871 |
0.0910 |
0.0948 |
0.0987 |
0.1026 |
0.1064 |
0.1103 |
0.1141 |
| 0.3 |
0.1179 |
0.1217 |
0.1255 |
0.1293 |
0.1331 |
0.1368 |
0.1406 |
0.1443 |
0.1480 |
0.1517 |
| 0.4 |
0.1554 |
0.1591 |
0.1628 |
0.1664 |
0.1700 |
0.1736 |
0.1772 |
0.1808 |
0.1844 |
0.1879 |
| 0.5 |
0.1915 |
0.1950 |
0.1985 |
0.2019 |
0.2054 |
0.2088 |
0.2123 |
0.2157 |
0.2190 |
0.2224 |
| 0.6 |
0.2257 |
0.2291 |
0.2324 |
0.2357 |
0.2389 |
0.2422 |
0.2454 |
0.2486 |
0.2517 |
0.2549 |
| 0.7 |
0.2580 |
0.2611 |
0.2642 |
0.2673 |
0.2704 |
0.2734 |
0.2764 |
0.2794 |
0.2823 |
0.2852 |
| 0.8 |
0.2881 |
0.2910 |
0.2939 |
0.2967 |
0.2995 |
0.3023 |
0.3051 |
0.3078 |
0.3106 |
0.3133 |
| 0.9 |
0.3159 |
0.3186 |
0.3212 |
0.3238 |
0.3264 |
0.3289 |
0.3315 |
0.3340 |
0.3365 |
0.3389 |
| 1.0 |
0.3413 |
0.3438 |
0.3461 |
0.3485 |
0.3508 |
0.3531 |
0.3554 |
0.3577 |
0.3599 |
0.3621 |
| 1.1 |
0.3643 |
0.3665 |
0.3686 |
0.3708 |
0.3729 |
0.3749 |
0.3770 |
0.3790 |
0.3810 |
0.3830 |
| 1.2 |
0.3849 |
0.3869 |
0.3888 |
0.3907 |
0.3925 |
0.3944 |
0.3962 |
0.3980 |
0.3997 |
0.4015 |
| 1.3 |
0.4032 |
0.4049 |
0.4066 |
0.4082 |
0.4099 |
0.4115 |
0.4131 |
0.4147 |
0.4162 |
0.4177 |
| 1.4 |
0.4192 |
0.4207 |
0.4222 |
0.4236 |
0.4251 |
0.4265 |
0.4279 |
0.4292 |
0.4306 |
0.4319 |
| 1.5 |
0.4332 |
0.4345 |
0.4357 |
0.4370 |
0.4382 |
0.4394 |
0.4406 |
0.4418 |
0.4429 |
0.4441 |
| 1.6 |
0.4452 |
0.4463 |
0.4474 |
0.4484 |
0.4495 |
0.4505 |
0.4515 |
0.4525 |
0.4535 |
0.4545 |
| 1.7 |
0.4554 |
0.4564 |
0.4573 |
0.4582 |
0.4591 |
0.4599 |
0.4608 |
0.4616 |
0.4625 |
0.4633 |
| 1.8 |
0.4641 |
0.4649 |
0.4656 |
0.4664 |
0.4671 |
0.4678 |
0.4686 |
0.4693 |
0.4699 |
0.4706 |
| 1.9 |
0.4713 |
0.4719 |
0.4726 |
0.4732 |
0.4738 |
0.4744 |
0.4750 |
0.4756 |
0.4761 |
0.4767 |
| 2.0 |
0.4772 |
0.4778 |
0.4783 |
0.4788 |
0.4793 |
0.4798 |
0.4803 |
0.4808 |
0.4812 |
0.4817 |
| 2.1 |
0.4821 |
0.4826 |
0.4830 |
0.4834 |
0.4838 |
0.4842 |
0.4846 |
0.4850 |
0.4854 |
0.4857 |
| 2.2 |
0.4861 |
0.4864 |
0.4868 |
0.4871 |
0.4875 |
0.4878 |
0.4881 |
0.4884 |
0.4887 |
0.4890 |
| 2.3 |
0.4893 |
0.4896 |
0.4898 |
0.4901 |
0.4904 |
0.4906 |
0.4909 |
0.4911 |
0.4913 |
0.4916 |
| 2.4 |
0.4918 |
0.4920 |
0.4922 |
0.4925 |
0.4927 |
0.4929 |
0.4931 |
0.4932 |
0.4934 |
0.4936 |
| 2.5 |
0.4938 |
0.4940 |
0.4941 |
0.4943 |
0.4945 |
0.4946 |
0.4948 |
0.4949 |
0.4951 |
0.4952 |
| 2.6 |
0.4953 |
0.4955 |
0.4956 |
0.4957 |
0.4959 |
0.4960 |
0.4961 |
0.4962 |
0.4963 |
0.4964 |
| 2.7 |
0.4965 |
0.4966 |
0.4967 |
0.4968 |
0.4969 |
0.4970 |
0.4971 |
0.4972 |
0.4973 |
0.4974 |
| 2.8 |
0.4974 |
0.4975 |
0.4976 |
0.4977 |
0.4977 |
0.4978 |
0.4979 |
0.4979 |
0.4980 |
0.4981 |
| 2.9 |
0.4981 |
0.4982 |
0.4982 |
0.4983 |
0.4984 |
0.4984 |
0.4985 |
0.4985 |
0.4986 |
0.4986 |
| 3.0 |
0.4987 |
0.4987 |
0.4987 |
0.4988 |
0.4988 |
0.4989 |
0.4989 |
0.4989 |
0.4990 |
0.4990 |
4【Excelで計算する場合】
 ○ Excelの表計算関数では,標準正規分布関数として =NORMSDIST(u) が利用できますが,この関数は右図のように ○ Excelの表計算関数では,標準正規分布関数として =NORMSDIST(u) が利用できますが,この関数は右図のように
P(−∞<z<u)の値を表しているので,正規分布表に書かれているP(0<z<u)の値に直すためには,左半分の面積P(z<0)すなわち0.5もしくは=NORMSDIST(0)を引きます.
例えば,P(0<z<1)の値は,=NORMSDIST(1)−0.5で得られます.
この関数は負の数に対しても利用でき,a<bのときP(a<z<b)の値は=NORMSDIST(b)−NORMSDIST(a)で求められます.
○ Excelで一般の正規分布(期待値0,標準偏差1とは限らない場合)の確率を計算するには,関数
NORMDIST(xの値, 期待値, 標準偏差, 1)
が使えます.上の図のような確率(曲線の下にある図形の面積)を求めるには,4番目の数字に1または TRUE を代入します.(確率密度関数の値 [グラフのy座標=縦線の長さ]を求めるときには,4番目の数字に0またはFALSEを代入します.)
なお,引数の順序に注意.また,第3引数が分散ではなく標準偏差であることにも注意:
|
【平均m,標準偏差σの正規分布】
○ 平均 m,標準偏差σの正規分布を記号 N(m,σ2)で表します.
- 正規分布(Normal Distribution)の頭文字がN
- よく使われる分散は標準偏差の2乗に等しく,N(m,σ2)の記号はN(平均,分散)と書いていることになります.
- N(m,σ2)という記号は,「平均m,標準偏差σの正規分布」というべきところを記号で短く表しただけのもので,数学の他の分野で使われるf(x,y)=zのような関数としての値があるわけではありません.
○ 正規分布と標準正規分布とは右図のように対応しており,正規分布で確率を求めるためには対応する標準正規分布に直して考えます. (一般の正規分布は種類が多いので個別に正規分布表というものを作っておくことはできません.)
変数 Xが平均 m,標準偏差σの正規分布に従うとき
z= ⇔ X=m+zσ
によって変数 zを求めると, zは標準正規分布になります.
【例題1】
変数Xが平均5,標準偏差3の正規分布に従うとき,
8<X<11
となる確率を求めてください.
 (解答) (解答)
=1,=2
(8=m+1σ,11=m+2σ)
だから,
P(8<X<11)=P(1<z<2)=0.4772−0.3413=0.1359
|
 ※ 記号N(m,σ2)では,2番目の引数が分散(=標準偏差の2乗)になっていることに注意.
※ 記号N(m,σ2)では,2番目の引数が分散(=標準偏差の2乗)になっていることに注意.
【例】
N(0,1) … 平均0,分散1(標準偏差1)の正規分布
N(10,32) … 平均10,分散9(標準偏差3)の正規分布
N(4,25) … 平均4,分散25(標準偏差5)の正規分布
【例題2】
変数Xが正規分布N(10,52)に従うとき,
P(5<X<25)
を求めてください.
 (解答) (解答)
=−1,=3
(5=m−1σ,25=m+3σ)
だから,
P(5<X<25)=P(−1<z<3)=0.4987+0.3413=0.8400
|
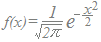

 ○ P(a<z<b)という記号によって,a<z<bとなる確率を表します.
○ P(a<z<b)という記号によって,a<z<bとなる確率を表します. ○ 曲線の下にある図形の面積全部で確率1を表しますが,グラフが左右対称になっているので,右半分,左半分の面積はそれぞれ0.5になります.
○ 曲線の下にある図形の面積全部で確率1を表しますが,グラフが左右対称になっているので,右半分,左半分の面積はそれぞれ0.5になります. 2【標準正規分布の累積関数の逆関数】
2【標準正規分布の累積関数の逆関数】 ○ Excelの表計算関数では,標準正規分布関数として =NORMSDIST(u) が利用できますが,この関数は右図のように
○ Excelの表計算関数では,標準正規分布関数として =NORMSDIST(u) が利用できますが,この関数は右図のように (解答)
(解答)
 (解答)
(解答) 1【標準正規分布の累積関数】
1【標準正規分布の累積関数】